Интегрирование рациональных выражений.

Первообразная. Неопределенный интеграл. Символика. Примеры.

Функция F(x) называется первообразной ф-ии f(x) на интервале (а;b),если для любого xЭ(a;b) выполняется равенство:

F’(x)=f(x) или (dF(x)=f(x)dx)

Множество первообразных функции f (x) называется неопределённым интегралом от этой функции и обозначается символом .
Как следует из изложенного выше, если F (x) - некоторая первообразная функции f (x), то , где C - произвольная постоянная. Функцию f (x) принято называть подынтегральной функцией, произведение f (x) dx - подынтегральным выражением.

Пример: .

Таблица неопределенных интегралов.

10.3. Таблица неопределённых интегралов.

	.		.
	.		.
	().		.
	.		.
	; .		.
	.
	.		.
	.		.
	.		.
	.		; .

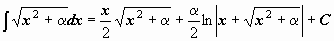Простейшие методы интегрирования. Метод интегрирования с

Использованием таблиц.

методы интегрирования: используя таблицу, разложение по членам(интегрирование по частям), подведение под знак дифференциала,подстановка(замена)

Метод интегрирования с использованием таблиц:

Непосредственно приводим уравнение к табличному виду неопределённых интегралов,например

∫dx/x²+5=∫dx/x²+(√5)²=1/√5*arctg(x/√5)+C

Простейшие методы интегрирования. Метод интегрирования подведением под знак дифференциала.

методы интегрирования: используя таблицу, разложение по членам(интегрирование по частям), подведение под знак дифференциала,подстановка(замена)

Пусть требуется вычислить Предположим, что существуют дифференцируемые функции и ,

такие, что тогда

Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.

Например. .

Простейшие методы интегрирования. Метод интегрирования разложением.

методы интегрирования: используя таблицу, разложение по членам(интегрирование по частям), подведение под знак дифференциала,подстановка(замена)

Метод интегрирования разложения:

∫(x+2)³dx=∫(x³+6x²+12x+8)=∫x³ dx+ ∫6x² dx+∫12xdx +∫8dx=x⁴/4+2x³ +6x² +8x+C

Метод интегрирования по частям. Две группы функций.

Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное.

Рекомендуется две группы функций:

I ∫xⁿ *sin(a*x)dx, ∫xⁿ *cos(a*x)dx,xⁿ=U ∫xⁿ *e^axdx

II ∫xⁿ *arcsin(a*x)dx, ∫xⁿ *arccos(a*x)dx, ∫xⁿ *arctg(a*x)dx, ∫xⁿ *arcctg(a*x)dx, ∫xⁿ *ln(a*x)dx U=arcsin(a*x)

Интегрирование выражений, содержащих квадратный трехчлен.

Рассмотрим интеграл , содержащий квадратный трехчлен в знаменателе подынтегрального выражения. Такой интеграл берут также методом подстановки, предварительно выделив в знаменателе полный квадрат

Пример:

∫(3*x-2)dx/5*x²-x+7 = 0,3*∫(10*x–1+1-2*10/3)dx/5*x²-x+7=[5*x²-x+7=t; (

10x-1)dx=dt)= 0,3*∫(10x-1)dx/(5*x²-x+7) +0,3*(1-20/3)∫dx/5*x²-x+7=

0,3*∫dt/t-1,7*∫dx/5(x-0,1)²+(1/100+7)=0,3*ln|5x²-x+7|- 17/50*∫dx/(x-0,1)²+(√699/√500)²=0,3*ln|5x²-x+7-17/50*√500/√699*arctg(x-1)* √500/√699

Интегрирование рациональных выражений.

Для интегрирования рациональной функции 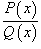, где P (x) и Q (x) -многочлены, используется следующая последовательность шагов:

1. Если дробь неправильная (т.е. степень P (x) больше степени Q (x)), преобразовать ее в правильную, выделив целое выражение;

Пример: x^4+3x^3-1/x^2+2x-5=x^2+x+3- (x-14)/x^2+2x-5 (деление столбиком)

1. Разложить знаменатель Q (x) на произведение одночленов и/или несократимых квадратичных выражений;
2. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
3. Вычислить интегралы от простейших дробей.

Теорема:любая дробно-рациональная функция раскладывается в сумму простейших дробно-рац. ф-ий. Вида: A/x-a;A/(x-a)^n;Bx+C/(x^2+px+q);Bx+C/(x^2+px+q)^n