Определение производной, ее физический и геометрический смысл.
Определение. Производной функции 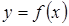 по аргументу х, называется предел отношения приращения функции
по аргументу х, называется предел отношения приращения функции 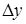 к приращению аргумента
к приращению аргумента 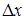 , когда
, когда 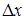 стремится к нулю.
стремится к нулю.
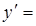
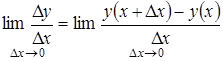 .
.
Так как мгновенной или истинной скоростью называется предел, к которому стремится 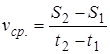 ,
,
когда интервал времени, на котором она измеряется, стремится к нулю, т.е. 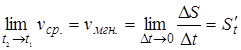 . Следовательно, физический смысл производной состоит в том, что производная есть скорость изменения данной функции.
. Следовательно, физический смысл производной состоит в том, что производная есть скорость изменения данной функции.
Рассмотрим график произвольной функции  :
:
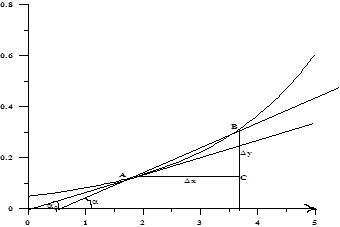 |
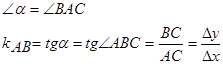

Если 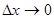 , то
, то 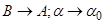 Прямая
Прямая 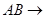 касательной α
касательной α 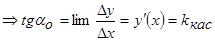
Следовательно, геометрический смысл производной состоит в том, что значение производной в точке касания равно тангенсу угла наклона касательной проведенной к графику функции в эту точку.
Процесс нахождения производной называется дифференцированием.
Для нахождения производной от данной функции 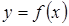 необходимо провести следующие действия: 1) дать аргументу x приращение
необходимо провести следующие действия: 1) дать аргументу x приращение 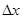 , вычислить наращенное значение функции
, вычислить наращенное значение функции 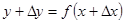 ;2)найти соответствующее приращение функции:
;2)найти соответствующее приращение функции: 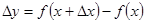 ;3) составить отношение приращения функции к приращению аргумента:
;3) составить отношение приращения функции к приращению аргумента: 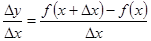 ;4) найти предел данного отношения при
;4) найти предел данного отношения при 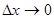 .
.
Вычислим производные от некоторых элементарных функций.
1. Производная постоянной равна нулю, т.е. если y=C, где C=const, то 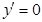 .
.
док-во: y=C, следовательно, при любом значении x 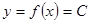
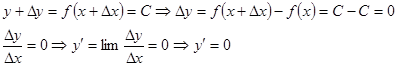
2. 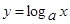 , то
, то 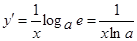
Доказательство:
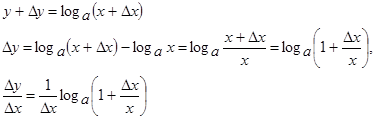
Домножим и разделим на x выражение, стоящее в правой части последнего равенства:
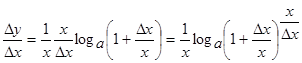
Обозначим величину 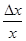 через α. Очевидно, что
через α. Очевидно, что 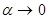 при
при 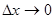 и данном x. Следовательно:
и данном x. Следовательно:
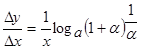 т.к.
т.к. 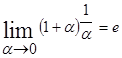
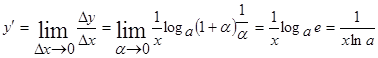 . ч.т.д.
. ч.т.д.
Доказывая аналогичными способами можно вывести производные всех элементарных функций.
Таблица производных элементарных функций:
1. 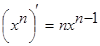 6.
6. 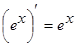
2. 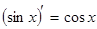 7.
7. 
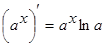
3. 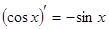
4. 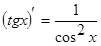 8.
8. 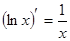
5. 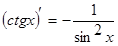 9.
9. 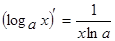
Для вывода производной от обратных тригонометрических функций используется теорема:
Теорема. Если для функции 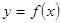 существует обратная функция,
существует обратная функция, 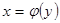 , которая в рассматриваемой точке y имеет производную
, которая в рассматриваемой точке y имеет производную 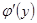 , отличную от нулю, то в соответствующей точке x,
, отличную от нулю, то в соответствующей точке x,
функция 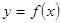 имеет производную
имеет производную 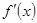 , причем
, причем
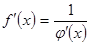 .
.
Выведем производную 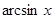 :
:
пусть 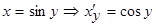 ; по теореме
; по теореме 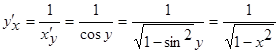
т.к. 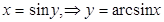 .
.
Следовательно 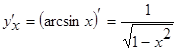 .
.
Аналогично выводятся формулы для остальных функций:
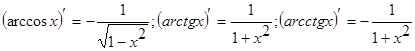
Правила дифференцирования.
Теорема 1. Постоянный множитель выносится за знак производной.
Доказательство:
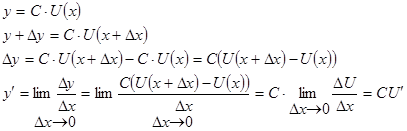
ч.т.д.
Теорема 2.
Производная суммы конечного числа дифференцируемых функций равна соответствуюшей сумме производныж этих функций.
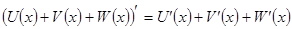
Теорема 3.
Производная от произведения двух дифференцируемых функций равна произведению производной первой фкункции на вторую пдюс произведение первой функции на производную от второй,т.е. если
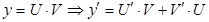
Докозательство:
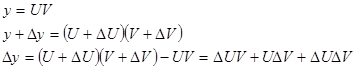
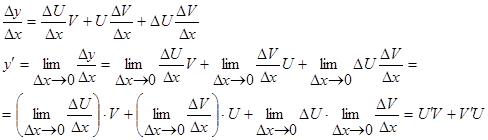
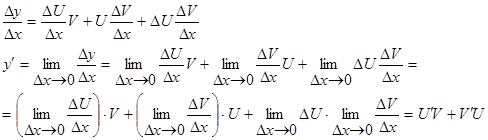
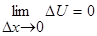 , т.к.
, т.к. 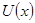 - дифференцируемая, непрерывная функция.
- дифференцируемая, непрерывная функция.
ч.т.д.
Теорема 4.
Производная частного равна дроби, у которой знаменатель есть квадрат знаменателя исходной дроби,а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателю, т.е.
если 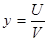 , то
, то 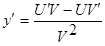 .
.
Теорема 5.
Если функция 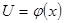 имеет в некоторой точке х производную
имеет в некоторой точке х производную 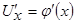 , а функция
, а функция 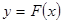
имеет при соответствующем значении U производную 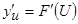 , тогда сложная функуция
, тогда сложная функуция

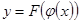 в указанной точке х, также имеет производную, которая равна
в указанной точке х, также имеет производную, которая равна


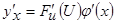
Приведем несколько примеров нахождения производных:
Пример 1.
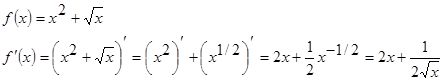
Пример 2.
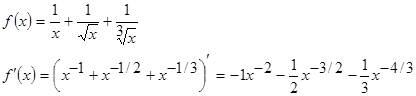
Пример 3.
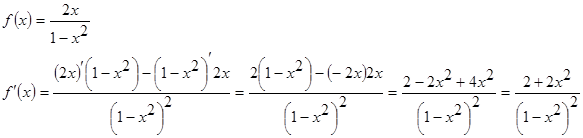
Пример 4. 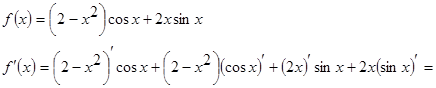
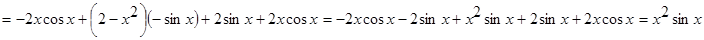
Пример 5.
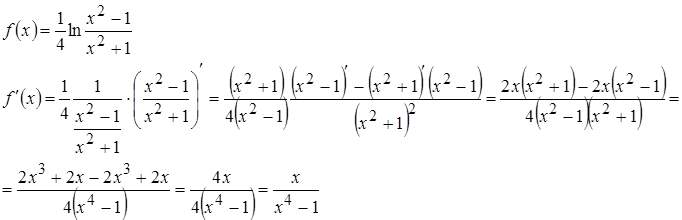
Пример 6
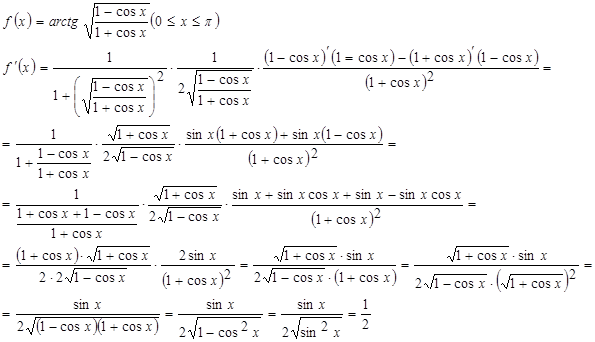
Понятие дифференциала
Рассмотрим функцию 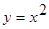 , тогда
, тогда
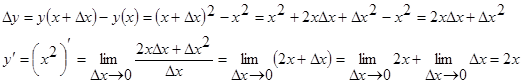
Следовательно 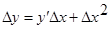
Определение: Главная часть 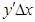 приращения функции называется дифференциалом этой функции и обозначается:
приращения функции называется дифференциалом этой функции и обозначается: 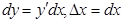 или
или 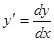 .
.
Приращение функции отличается от дифференциала функции на величину бесконечно малую, поэтому в приближенных вычислениях пользуются приближенным равенством 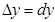 , или в развернутом виде
, или в развернутом виде 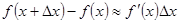 .
.
Пример: Пусть 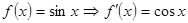
Из равенства 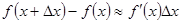 следует равенство
следует равенство 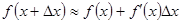 ,
,
используя его, вычислим значение 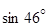 . Положим
. Положим 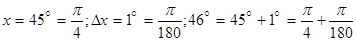
так как 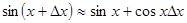 , получим
, получим
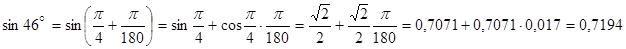
Задача нахождения дифференциала функции равносильна нахождению производной, т.к. умножив последнюю на дифференциал аргумента получим дифференциал функции, следовательно большинство теорем и формул, относящихся к производным сохраняют свою силу и для дифференциалов.
Пример. Найти дифференциал функции 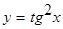 .
.
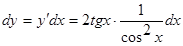 .
.
Пример. 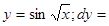 ?
?
Пусть 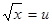 , тогда
, тогда 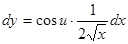 , но
, но 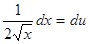 , поэтому
, поэтому 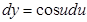 или
или
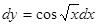 .
.