Министерство образования и науки Российской Федерации
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра высшей математики
ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ
Индивидуальные задания для семестровой работы

Волгоград 2011
УДК
Рецензент
А.Е. Годенко
Издаётся по решению редакционно-издательского отдела
Волгоградского государственного технического университета.
определённые интегралы: Индивидуальные задания для семестровой работы / сост. В.И.Шушков, В.Н.Поляков.
Волгоград: ИУНЛ ВолгГТУ, 2011.-23с.
В индивидуальных заданиях «Определённые интегралы» представлены 25 вариантов индивидуальных заданий. В каждом задании даны определённые интегралы, несобственные интегралы, геометрические и физические задачи, решаемые с помощью определённых интегралов. Предназначено для студентов первого курса всех специальностей и всех форм обучения.
©Волгоградский государственный
Технический университет
Вариант 1
1. Вычислить интегралы: а)  , b)
, b)  , с)
, с)  , d)
, d)  .
.
2. Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3. Вычислить площадь плоской фигуры ограниченной линиями:
a) y=4-x2, y=x2-2x-3; b)  ,
,  .
.
4. Вычислить объём тела, ограниченного поверхностями:
 , -2≤z≤2, по площадям параллельных сечений.
, -2≤z≤2, по площадям параллельных сечений.
5. Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=5+4x-x2, y=0, вокруг оси ox.
6. Вычислить массу пластинки ограниченной линиями: y=x2, y=4,с поверхностной плотностью пропорциональной 2y.
7. Вычислить работу по выкачиванию жидкости, с плотностью обратно пропорциональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями: x2+y2-z2=0, 0≤z≤4.
8. Вычислить силу давления воды на плотину, имеющую форму параболического сегмента: y=x2, y=4.
9. Вычислить силу давления воды на пластинку, имеющую форму равнобокой трапеции с основаниями 8 и 4 метра и высотой 4 метра, опущенную вертикально в воду на глубину 5 метров от поверхности воды до верхнего большего основания трапеции.
10. Вычислить координаты центра тяжести плоской фигуры ограниченной линиями x=0, y=0, x=(y-2)2.
Вариант 2
1. Вычислить интегралы: а)  , b)
, b)  , c)
, c)  ,
,
d)  .
.
2. Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3. Вычислить площадь плоской фигуры ограниченной линиями:
a) x=4-y2, x=y2-2y-3; b)  ;
; 
4. Вычислить объём тела, ограниченного поверхностями
 , -2≤z≤2, по площадям параллельных сечений.
, -2≤z≤2, по площадям параллельных сечений.
5. Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями x=5+4y-y2, y=0, вокруг оси oy.
6. Вычислить массу пластинки ограниченной линиями: y2=x, x=4,с поверхностной плотностью пропорциональной 2x.
7. Вычислить работу по выкачиванию жидкости, с плотностью обратно пропорциональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями: x2+y2-z2=1, 0≤z≤4.
8. Вычислить силу давления воды на плотину, имеющую форму параболического сегмента: y=x2-16, y=0.
9. Вычислить силу давления воды на пластинку, имеющую форму равнобокой трапеции с основаниями 8 и 4 метра и высотой 4 метра, опущенную вертикально в воду на глубину 5 метров от поверхности воды до верхнего меньшего основания трапеции.
10. Вычислить координаты центра тяжести криволинейного треугольника ограниченного осями координат и параболой
y=(x-2)2.
Вариант 3
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 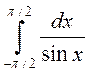 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
y=x, y=2x, y=3; b)  ,
,  .
.
4) Вычислить объём тела, ограниченного поверхностями
 , 1≤z≤2, по площадям параллельных сечений.
, 1≤z≤2, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=1-x2, y=0, вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y=(x-1)2, y=1,с поверхностной плотностью пропорциональной y.
7) Вычислить работу по выкачиванию жидкости, с плотностью пропорциональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями: z=x2+y2, 0≤z≤4.
8) Вычислить силу давления воды на плотину, имеющую форму кругового сегмента: y2+x2=1, y≤0.
9) Вычислить силу давления воды на пластинку, имеющую форму равностороннего треугольника, сторона которого равна 4 метра, опущенную вертикально в воду вершиной вниз на глубину 5 метров от поверхности воды до основания.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=x2-4x, y=0.
Вариант 4
1. Вычислить интегралы: а)  , b)
, b) 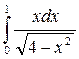 , с)
, с)  ,
,
d)  .
.
2. Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3. Вычислить площадь плоской фигуры ограниченной линиями:
а) y=x, y=2x; y=4; b)  ,
, 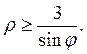
4.Вычислить объём тела, ограниченного поверхностями
 , -2≤z≤2, по площадям параллельных сечений.
, -2≤z≤2, по площадям параллельных сечений.
5. Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=4x-x2, y=0, вокруг оси ox.
6. Вычислить массу пластинки ограниченной линиями: y=4-x2, y=0,с поверхностной плотностью пропорциональной y.
7. Вычислить работу по выкачиванию жидкости, с плотностью пропорци- ональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями: x2+y2-z2=1, 0≤z≤4.
8. Вычислить силу давления воды на плотину, имеющую форму параболического сегмента: y=x2-4, y=0.
9. Вычислить силу давления воды на пластинку, имеющую форму равнобокой трапеции с основаниями 6 и 2 метра и высотой 2 метра, опущенную вертикально в воду на глубину 6 метров от поверхности воды до верхнего меньшего основания трапеции.
10. Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями x=0, y=0, x=(y+2)2.
Вариант 5
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
y=0,25x2+2, 5x-8y+14=0, b)  ,
,  .
.
4) Вычислить объём тела, ограниченного поверхностями 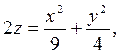 0≤z≤5, по площадям параллельных сечений.
0≤z≤5, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=1+x2, y=4, вокруг оси oх.
6) Вычислить массу пластинки ограниченной линиями: x=1 y  , y=0,с поверхностной плотностью равной x3/2 .
, y=0,с поверхностной плотностью равной x3/2 .
7) Вычислить работу по выкачиванию жидкости из ёмкости, поверхность
которой описывается уравнением  0≤z≤5; плотность жидкости 700кг/м3.
0≤z≤5; плотность жидкости 700кг/м3.
8 Вычислить силу давления бензина, находящегося в цилиндрическом баке высотой h=3,5м, на его стенки, если плотность бензина 900кг/м3.
9. Какую силу давления испытывает прямоугольная пластинка длиной 2м и шириной 1м, если она наклонена к горизонтальной поверхности жидкости под углом 30о и её большая сторона находится на глубине 5м.
10. Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y2=x3, x=2.
Вариант 6
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  d)
d) 
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 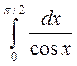 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) x=-2y2, x=1-3y2; b)  .
.  .
.
4) Вычислить объём тела, ограниченного поверхностями
 , 5≤z≤10, по площадям параллельных сечений.
, 5≤z≤10, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=(x-1)2, x=2, y=0, вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: x=9-y2, x=2, y=0,с поверхностной плотностью пропорциональной y.
7) Вычислить работу по выкачиванию жидкости, с плотностью, пропорциональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями:  , z=0, z=4.
, z=0, z=4.
8) Вычислить силу давления воды на плотину, имеющую форму кругового сегмента: y2+x2=1, y≤0, х≥0.
9) Вычислить силу давления воды на пластинку, имеющую форму круга радиуса 1м, центр которой находится на глубине 5м от поверхности воды.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями x =0, y=1, x=  .
.
Вариант 7
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b) 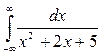 .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) x=y2, x=(3/4)y2+1; b)  .
.
4) Вычислить объём тела, ограниченного поверхностями  , 1≤z≤2, по площадям параллельных сечений.
, 1≤z≤2, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=x3, y=  , вокруг оси ox.
, вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y2=(x-1)2, y=1,с поверхностной плотностью пропорциональной y.
7) Вычислить работу, которую надо затратить, чтобы выкачать воду из цистерны, ограниченной поверхностями y2=4z, x=  1, z=2.
1, z=2.
8) Вычислить силу давления воды на плотину, имеющую форму полукруга, диаметр которого 6м и находится на поверхности воды.
9) Вычислить силу давления воды на пластинку, имеющую форму треугольника с высотой 2м, основание которой 3м параллельно поверхности воды, а противоположная вершина находится на поверхности воды.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями 16y=x2 , x= 4, y=0.
Вариант 8
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) x=4-y2, x=y2-2y; b) 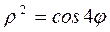 .
.
4) Вычислить объём тела, ограниченного поверхностями x2+y2=1, y=0, z=0, x+z-1=0, x-z+1=0, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=x2/2+2x+2, y=2 вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: y=1/x, y=0, x=2, с поверхностной плотностью ky, где k- коэффициент пропорциональ-ности.
7) Вычислить работу по выкачиванию жидкости, плотности 0,8г/см3, из целиком заполненного бака, если бак имеет форму параболоида вращения, расположенного вершиной вниз и имеющего глубину 10м и радиус отверстия 5м. 
8) Вычислить силу давления жидкости на пластинку, имеющую форму прямоугольного треугольника с катетами 5см и 12см, опущенную вертикально вершиной вниз, в жидкость плотности 700кг/м3 так, что катет 5см находится на глубине 25см.
9) Вычислить силу давления воды на вертикально погружённую часть пластинки, имеющей форму эллипса с полуосями 4м и 3м так, что малая ось эллипса находится на поверхности воды.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y2=2x, x+y=4.
Вариант 9
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры, ограниченной линиями:
а) y=(x+1)2, y2=x+1, b) 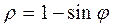 ,
,  .
.
4) Вычислить объём тела, ограниченного поверхностями z=0, z=  , x2/27+y2=1, y
, x2/27+y2=1, y  0, по площадям параллельных сечений.
0, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=2x-x2, y=-x+2, x=0 вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y= 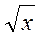 , y=x-2, x=0с поверхностной плотностью пропорциональной 2x.
, y=x-2, x=0с поверхностной плотностью пропорциональной 2x.
7) Вычислить работу по выкачиванию жидкости, с плотностью 700кг/м3, из вертикального цилиндрического резервуара высотой 4м и радиусом основания 3м.
8) Вычислить силу давления воды на плотину, имеющую форму прямоугольника с основанием 10м и высотой 8м.
9) Вычислить силу давления воды на пластинку, имеющую форму круга радиуса 2м вертикально опущенную в жидкость плотности 800кг/м3. Центр пластинки находится на глубине 10м.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями 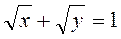 ,x=0, y=0.
,x=0, y=0.
Вариант 10
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 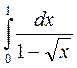 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=(x+1)2, y2=x+1; b)  ,
,  .
.
4) Вычислить объём тела, ограниченного поверхностями x=y  , x=0, y≥0,
, x=0, y≥0, 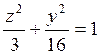 , по площадям параллельных сечений.
, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями x2+(y-2)2=1, вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y=6x-x2-7, y=x-3,с поверхностной плотностью пропорциональной 3x.
7) Вычислить работу по выкачиванию жидкости, с плотностью 1т/м3 из усечённого конуса, высота которого равна 2м, радиуса нижнего основания 0,5м, верхнего-1м. Жидкость полностью заполняет конус.
8) Вычислить силу давления воды на плотину, имеющую форму параболического сегмента: y =2x2, y=8.
9) Вычислить силу давления воды на пластинку, имеющую форму трапеции с основаниями 16 и 8 метров и высотой 4 метра, опущенную вертикально в воду вершиной вниз на глубину 10 метров от поверхности воды до меньшего основания.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y2=2x, x+y=4.
Вариант 11
1) Вычислить интегралы: а)  ; b)
; b) 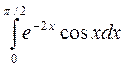 ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=x2, y=6-x, y=0 x≥0; b)  ..
..
4) Вычислить объём тела, ограниченного поверхностями x2+y2=(z-1)2, z=0, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями xy=1, y=0, x=1, x=2 вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: x2-y2=1, x=0, y=0,y=1 с поверхностной плотностью пропорциональной 3y.
7) Какую работу нужно произвести, чтобы насыпать кучу песка (плотность песка 2300кг/м3) в форме усечённого конуса высоты  м, имеющего радиусы оснований 2м и 1м (песок поднимается с поверхности земли, на которой покоится большее основание конуса).
м, имеющего радиусы оснований 2м и 1м (песок поднимается с поверхности земли, на которой покоится большее основание конуса).
8) Вычислить силу давления бензина на боковые стенки кругового цилиндра, высота которого 2м, а диаметр основания 1м. Плотность бензина 700кг/м3.
9) Пластина, имеющая форму кольца с радиусами 3м и 1м, вертикально погружена в жидкость плотности 0,8т/м3. Центр кольца находится на глубине 10м. Найти силу давления на пластину.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями:  , x=0, y=0, x≥0, y≥0.
, x=0, y=0, x≥0, y≥0.
Вариант 12
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 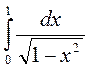 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=(x-2)3, y=4x-8; b)  ,
,  .
.
4) Вычислить объём тела, ограниченного поверхностями x2+z2=1, y2+z2=1, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=1-(x-4)2, y=0, вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: x=y2(y-1), x=0с поверхностной плотностью пропорциональной y/2.
7) Котёл имеет форму параболоида вращения с радиусом 2м и глубиной 4м. Он наполнен жидкостью, удельный вес которой 0,8г/см3. Вычислить работу, которую нужно совершить, чтобы выкачать жидкость из котла.
8) Вычислить силу давления воды на вертикальную плотину, имеющую форму параболического сегмента, высота которого 16м, а высота совпадает с уровнем воды и имеет длину 40м.
9) Круглая пластина радиуса 1м вертикально опущена целиком в жидкость плотности 0,8г/см3. Центр пластины находится на глубине 4м. Найти силу давления на пластину.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y2=x3, x=1.
Вариант 13
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y2 +x=4, y2-3x=12; b) 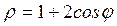 .
.
4) Вычислить объём тела, ограниченного поверхностями  , y=20, по площадям параллельных сечений.
, y=20, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями 2y=x2, y=|x|, вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y=  , y=0, x=2 с поверхностной плотностью пропорциональной 2
, y=0, x=2 с поверхностной плотностью пропорциональной 2  .
.
7) Котёл, имеющий форму полушара радиуса 2м, наполнен водой. Какую работу нужно затратить, чтобы выкачать воду из этого котла?
8) Вычислить силу давления воды на плотину имеющую форму части кругового сегмента: y2+x2=1, y≤0, 0≤х≤0,5.
9) Вычислить силу давления воды на пластинку, имеющую форму равнобедренного треугольника, боковая сторона которого равна 4м, а угол при вершине равен 30о, опущенную вертикально в воду так, что боковая сторона находится на поверхностном уровне.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=4-x2, x2+y2=1.
Вариант 14
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b) 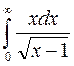 .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=ln(1+x), y=-xe-x, x=1; b) 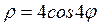 .
.
4) Вычислить объём тела, ограниченного поверхностями y2+x+z=1, x=0, y=0, z=0, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=|x-4|-2, y=0, вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: y=x2, x+y=3/4,с поверхностной плотностью пропорциональной 4x.
7) Вычислить работу, которую надо затратить, чтобы выкачать воду из котла, имеющего форму параболоида вращения, обращенного вершиной вверх. Радиус основания 5м, высота 10м.
8) Вычислить силу давления воды на плотину имеющую форму части кругового сегмента: y2+x2=1, y≤0, -1≤х≤-0,75.
9) Вычислить силу давления воды на пластинку, имеющую форму равностороннего треугольника, сторона которого равна 4 метра, опущенную вертикально в воду вершиной вниз на глубину 5 метров от поверхности воды до основания.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=x2-4x-4, y=0.
Вариант 15
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 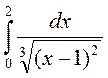 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=x-x2, y=x  ; b)
; b) 
4) Вычислить объём тела, ограниченного поверхностями  , z=5, по площадям параллельных сечений.
, z=5, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями x2+(y-2)=1 вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: x2/4+y2=1, x=0 y=0с поверхностной плотностью пропорциональной 10x.
7) Вычислить работу по выкачиванию жидкости, с плотностью пропорциональной расстоянию от поверхности уровня жидкости, из ёмкости, поверхность которой описывается уравнениями: z=x2+y2, 0≤z≤4.
8) Вычислить силу давления воды на плотину имеющую, форму части кругового сегмента: y2+x2=1, y≤0, -0,5≤х≤0,5.
9) Вычислить силу давления воды на пластинку, имеющую форму равностороннего треугольника, сторона которого равна 4 метра, опущенную вертикально в воду вершиной вниз на глубину 5 метров от поверхности воды до основания.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y2=2х, y≥0, x=1
Вариант 16
1) Вычислить интегралы: а)  ; b)
; b) 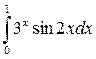 ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b) 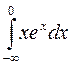 .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a)y=e-x, x=0 y=0, x=1; b) 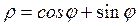 .
.
4) Вычислить объём тела, ограниченного поверхностями  , z/6=x/3, z=0, по площадям параллельных сечений.
, z/6=x/3, z=0, по площадям параллельных сечений.
5. Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=  x=1, y=0, вокруг оси ox.
x=1, y=0, вокруг оси ox.
6. Вычислить массу пластинки ограниченной линиями: y=  , x=1 y=0с поверхностной плотностью пропорциональной 5x3.
, x=1 y=0с поверхностной плотностью пропорциональной 5x3.
7. Вычислить работу по выкачиванию воды из конического сосуда, основание которого горизонтально и расположено ниже вершины, если радиус основания равен 10м и высота равна 5м.
8. Вычислить силу давления на дно горизонтально расположенной цистерны и заполненной бензином на 3/4 диаметра. Плотность бензина 800кг.м3. Диаметр цистерны 4м.
9. Вычислить силу давления воды на вертикальную стенку, имеющую форму эллипса с полуосями 10м и 5м, большая ось которого находится на поверхности воды.
10. Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=cosx, y=0, - 
Вариант 17
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d).
; d). 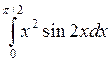
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=x2/2, 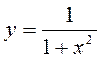 ; b)
; b)  .
.
4) Вычислить объём тела, ограниченного поверхностями
 , z=0, по площадям параллельных сечений.
, z=0, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линией, x2-xy+y2=1 вокруг оси ox.
6) Вычислить массу пластинки ограниченной линиями: y2=4x, y=0, y≥0, x=1с поверхностной плотностью пропорциональной 7x2.
7) Какую работу нужно затратить, чтобы насыпать кучу песка конической формы с диаметром 1м и высотой 1м, если удельный вес равен 2,5г/см3.
8) Вычислить силу давления воды на плотину, имеющую форму параболического сегмента, основание которого равно 1м и расположено на поверхности воды, а вершина находится на глубине 8м.
9) Вычислить силу давления воды на пластинку, имеющую форму треугольника, основание которого равно 2м и расположено на глубине 5м, а вершина находится на глубине 10м.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями x2+4y=16, y=0, x=0.
Вариант 18
1) Вычислить интегралы: а)  ; b);
; b); 
c)  ; d)
; d) 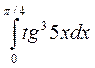 .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b) 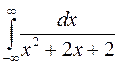 .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) x=y2(y-1), x=0; b)  .
.
4) Вычислить объём тела, ограниченного поверхностями y=x2+5z2, y=5, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=(x-1)(x-2), y=0, вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями:  ,x=0, y=0 с поверхностной плотностью пропорциональной 4x2.
,x=0, y=0 с поверхностной плотностью пропорциональной 4x2.
7) Вычислить работу по выкачиванию воды из конической ямы, диаметр основания которой равен 4м, а глубина 6м.
8) Вычислить силу давления воды на плотину, имеющую форму параболического сегмента: y=x4-16, длина хорды равна 4м.
9) Найти силу давления воды на пластинку, имеющую форму трапеции с верхним основанием 40м нижним 20м и высотой 8м, опущенную вертикально в воду так, что верхнее основание параллельно поверхности воды и находится на глубину 5 метров от поверхности воды.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=-3x2+4x, y=0.
Вариант 19
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d) 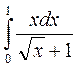 .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=x, y=1/x, y=10/3-x, x≥1; b) 
4) Вычислить объём тела, ограниченного поверхностями  , по площадям параллельных сечений.
, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y2=4x, y=x, вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: x2+y2/25=1, y=0, x=0с поверхностной плотностью пропорциональной 3x.
7) Шар радиуса 1м погружен полностью в воду. Какую работу надо затратить, чтобы извлечь шар из воды, если удельный вес шара и воды равен 1г/см3
8) В дне цилиндрического сосуда, площадь основания которого 100см2, а высота 30см, имеется отверстие. Найти площадь этого отверстия, если известно, что вода, наполняющая сосуд, вытекает из него в течении 2минут.
9) Найти величину давления на каждую из сторон прямоугольника, вертикально погруженного в воду, если известно, что основание его равно 5м, высота 4м, верхнее основание параллельно поверхности воды и находится на глубине 5м.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями x2/3+y2/3, y≥0.
Вариант 20
1) Вычислить интегралы: а)  ; b)
; b)  ; c)
; c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а)  ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=  y=2; b)
y=2; b) 
4) Вычислить объём тела, ограниченного поверхностями  , 0≤x≤6, по площадям параллельных сечений.
, 0≤x≤6, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями y=1/(1+x2), y=0, x=0 вокруг оси oy.
6) Вычислить массу пластинки ограниченной линиями: y2=x/2, y=0, y≥0, x=2с поверхностной плотностью пропорциональной  .
.
7) Цилиндрическая цистерна радиуса 2м наполовину наполнена жидкостью, вес которой равен G. Ось цистерны горизонтальна. Какую работу надо произвести, чтобы выкачать жидкость через люк в верхней части цистерны.
8) Вычислить силу давления воды на пластинку, имеющую форму полуэллипса, меньшая ось которого находится на поверхности жидкости. Большая полуось эллипса 6м, малая-2м.
9) Определить расход жидкости через водослив прямоугольного сечения. Высота водослива 10м ширина 20м.
10) Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями y=1-x2/4, y=0.
Вариант 21
1) Вычислить интегралы: а)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2) Исследовать несобственные интегралы на сходимость. Если интеграл сходится, то вычислить его: а) 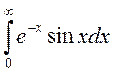 ; b)
; b)  .
.
3) Вычислить площадь плоской фигуры ограниченной линиями:
a) y=|log2x|, y=0, x=1/2,x=2; b)  .
.
4) Вычислить объём тела, ограниченного поверхностями z=x2+y2, z2=x2+y2, по площадям параллельных сечений.
5) Вычислить объём тела, полученного при вращении плоской фигуры ограниченной линиями 2y=(x-1)2, 2y=1, вокруг оси oy.
6) Вычис