Цели и задачи урока:
- научить учащихся выделять однородные тригонометрические уравнения среди других видов тригонометрических уравнений; научить учащихся решать однородные тригонометрические уравнения;
- развивать умение ориентироваться в видах тригонометрических уравнений, умение логически анализировать и подбирать необходимый метод решения известных видов тригонометрических уравнений;
- воспитывать умение высказывать свои предположения, умение выслушивать мнение одноклассников.
План урока:
| № | Этап урока | Содержание | Время (мин) |
| Организационный момент | Объявление темы урока, постановка целей. | ||
| Актуализация опорных знаний | Тестирование с последующей проверкой | ||
| Изучение нового материала | Ввод понятия однородного уравнения первой и второй степени, методика решения данных уравнений. | ||
| Закрепление пройденного материала | Работа с использованием интерактивной доски, а также материала ЦОР https://school-collection.edu.ru/ | ||
| Домашнее задание | Запись домашнего задания. Раздача карточек с творческим домашним заданием желающим. | ||
| Подведение итогов | Повторение основных моментов урока. Оценка урока учащимися. |
Ход урока:
1. Организационный момент.
Приветствие учащихся, сообщение темы урока, объявление целей и задач урока.
2. Актуализация опорных знаний и умений учащихся.
На доске написаны тестовые задания с вариантами ответов. Учащиеся самостоятельно выполняют предложенные задания на заранее приготовленных листочках. Время выполнения 5 мин. Далее ребята обмениваются работами с соседом по парте, выполняем проверку тестовых заданий, обсуждая правила их выполнения.
|
|
1. Решите уравнение
2. Найти наименьший положительный корень уравнения
а) 
Проверив, ребята выставляют друг другу оценки и сдают работы учителю.
3. Объяснение нового материала.
Простейшие тригонометрические уравнения мы решать умеем, умеем решать и уравнения, сводимые к квадратным, с помощью замены. Например:
К доске вызывается один из учащихся и решает данное уравнение методом замены.
Совместно оцениваем его работу.
Учитель предлагает ребятам следующее уравнение:
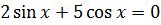
Что вы можете сказать о этом уравнении?
Ученики замечают, что в данном уравнении две тригонометрические функции, причем степень у них одинаковая и известные методы решения применить к этому уравнению не получится.
Учитель обращает внимание на то, что правая часть уравнения равна нулю.
Некоторые ребята сразу же предположат, что 
и 
равны нулю. С помощью учителя ученики проверяют предположение о том, могут ли эти две функции быть равны нулю одновременно. Оказывается, нет, так как при этом не выполняется основное тригонометрическое тождество.
Учитель вводит понятие однородного тригонометрического уравнения первой степени. Ребята записывают определение в тетрадь.
Как же решается данное уравнение?
Т.к. мы уже сказали, о том, 
, мы можем разделить данное уравнение, на и получим уравнение
такие уравнения мы решать умеем.
Ребята продолжают решение самостоятельно, сверяем ответы
Отлично! Запишем следующее уравнение:
Сразу обращаем внимание на то что уравнение состоит из двух тригонометрических функций, степени у них одинаковые и правая часть уравнения равна нулю, т.е уравнение однородное.
|
|
Еще на что нужно обратить внимание? Аргумент функций одинаков.
Учащиеся предполагают что уравнение надо на что-то поделить. На что? На 
Обязательно оговариваем, что 
К доске выходит более подготовленный учащийся и продолжает решение уравнения.
После деления получим
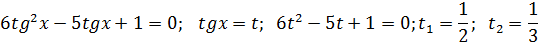
Ответ: 
Остальные учащиеся выполняют решение уравнения в тетради, сверяясь с доской.
Молодцы! Ребята, а можно ли применить в данных случаях деление на синус? Подумав, ученики отвечают, что возможно, но при этом в уравнение получится другая тригонометрическая функция – котангенс.
4. Закрепление пройденного материала.
Работа ведется с использованием интерактивной доски и материала из единой коллекции цифровых образовательных ресурсов https://school-collection.edu.ru/catalog/rubr/ef89b829-d575-4668-84e3-20f8abf11bcf/112990/?interface=pupil&class[]=53&class[]=54&subject[]=16&subject[]=17
Интерактивный ресурс «Однородные тригонометрические уравнения» состоит из трех частей
- повторение изученной теории (2-3 мин)
- практическая работа – предложенные примеры разбираются у доски и записываются в тетради (5 мин)
-самостоятельная работа учащихся по решению уравнений (5 мин)
-самопроверка и оценка своей работы – учитель на интерактивной доске показывает правильное решение уравнения (2-3 мин)
5. Домашнее задание: задания по учебнику №119(б), №120(в),№124(в,г),№126(в)
Творческое домашнее задание раздается на карточках желающим ученикам
6. Подведение итогов урока.
Еще раз повторяем, какие тригонометрические уравнения называются однородными, алгоритмы решения уравнений первой и второй степени.
|
|
Учитель учащихся просит оценить урок по 5 балльной шкале. Интересен ли был урок? Все ли в ходе урока ребята поняли или нет?