Основные характеристики функции

ВВЕДЕНИЕ В МАТ. АНАЛИЗ

Понятие функции

Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу х X сопоставляет один и только один элемент у Y, называется функцией и записывается у = f(x) или f: X Y

Говорят еще, что функция отображает множество X на множество У.

Множество X называется областью определения функции и обозна­чается D (f). Множество всех у из Y называется множеством значений функции и обозначается E(f).

Способы задания функций

Пусть задана функция . Если элементами множеств X и Y являются действительные числа, то функцию называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для крат­кости будем именовать их просто функциями и записывать у = f(x).

Переменная х называется при этом аргументом или независимой пе­ременной, a y — функцией или зависимой переменной (от х).

Графиком функции у = f(x) называется мно­жество всех точек плоскости О ху, для каждой из которых х является значением аргумента, а у — соответствующим значением функции.

Наиболее часто встречаются три способа зада­ния функции: аналитический, табличный, графический.

Функции могут быть записаны:

а) в декартовых координатах:

· в явном виде ;

· в неявном ;

· в параметрическом виде 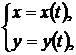где t вспомогательный параметр.

б) в полярных координатах.

Полярная система координат задается точкой О - полюсом, и лучом р – полярной осью. Числа r и j называются полярными координатами точки М. Записывают , при этом r называется полярным радиусом, j - полярным углом.

Для того чтобы установить связь между полярной и декартовой системой координат необходимо совместить начало координат декартовой системы с полюсом, а полярную ось с положительно направленной осью Ох (Рис. 1). Тогда координаты точки в двух различных системах координат связываются формулами:

Рис. 1

Основные характеристики функции

Функция у = f(x), определённая на множестве D, называется чётной, если для выполняется условие ; нечётной, если для выполняется условие (график чётной функции симметричен относительно оси О у, график нечётной относительно начала координат).

Пусть функция y = f(x) определена на множестве D и пусть D₁ D.
Если для любых значений аргументов из неравенства вытекает неравенство:

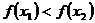· , то функция называется возрастающей на множестве D₁;

· , то функция называется неубывающей на множестве D₁;

· , то функция называется убывающей множестве D₁;

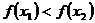· , то функция называется невозрастающей на множестве D₁.

Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D₁ называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности.

Функцию у = f(x), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М > О, что
для всех х D выполняется неравенство .

Функция у = f(x), определенная на множестве D, называется перио­дической на этом множестве, если су­ществует такое число Т > 0, что при каждом х D значение (х + Т) D и f(x + Т) = f(x). При этом число Т называется периодом функции.

Замечание: обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству f(x + Т) = f(x).

Обратная функция

Пусть задана функция у = f(x) с областью определения D и множеством значений Е. Если каждому значению у Е соответствует единственное значение х D, то определена функ­ция х = φ (у) с областью определения Е и мно­жеством D. Такая функ­ция φ (у) называется обратной к функции f(x). Про функции у = f(x) и х =φ (у) говорят, что они являются взаимно об­ратными.

Замечание:

1) любая строго монотонная функция имеет обратную;

2) графики взаимообратных функций симметричны относительно биссектрисы первого и второго координатных углов.

Сложная функция

Пусть задана функция u = y (x), отображающая множество X в множество U, и пусть задана функция y = f (u) отображающая множество U в множество Y. Тогда последовательное отображение ставит в соответствии каждому элементу элемент такой, что .