Содержание
Введение………………………………………………………………………….3
1 Дисперсный состав пыли....................................................................................4
2 Определение параметров дисперсного состава пыли древесной..................8
3 Подбор пылеочистительного аппарата.............................................................10
4 Расчет эффективности очистки циклона с обратным конусом ЦОК-10…..11
5 Циклон с обратным конусом типа ЦОК-10………………………………...14
Заключение……………………………………………………………………..16 Список литературы………………………………………………………….…17
Приложение 1.........................................................................................................18
Приложение 2.........................................................................................................19
Приложение 3.........................................................................................................20
Введение
Ни для кого не секрет, что производственные процессы загрязняют атмосферный воздух взвешенными твердыми или жидкими частицами (аэрозольные частицы, газы, пары и т.д.).
Очистка загрязненного воздуха является одним из ключевых мероприятий по защите воздушного бассейна, так как различные твёрдые и жидкие частицы, находящиеся в составе выбрасываемого воздуха могут привести к ухудшению экологических и экономических условий, что непосредственно приводит к преждевременному износу объектов жилищно-коммунального хозяйства, промышленных объектов и, конечно же, наносит значительный ущерб здоровью человека.
Для улавливания взвешенных частиц применяются газо-пылеулавливающие оборудования различных типов, среди которых значительное место занимают циклонные аппараты, являющиеся наиболее актуальными для сухого механического пылеулавливания.
В зависимости от свойства и от дисперсного состава частиц пыли циклоны чаще используются в качестве первой ступени очистки воздуха.
Целью курсового проекта является – расчет эффективности очистки циклона с обратным конусом типа ЦОК – 10.
Цель была достигнута благодаря выполнению следующих задач:
Ø определение параметров дисперсного состава пыли (пыль древесная)
Ø изучение сведений об устройстве и работе пылеулавливающего оборудования;
Ø расчет эффективности очистки запылённого воздуха в циклоне с обратным конусом типа ЦОК-10.
Дисперсный состав пыли
Дисперсность частиц промышленных аэрозолей, или пыли, характеризуется совокупностью размеров всех составляющих частиц.
Как правило, состав пыли полидисперсен, т.е. содержит частицы различных размеров. Монодимерные пыли, т.е. те, которые содержат частицы одного размера (или узкого интервала размеров) частиц, практически не встречаются. Таким образом, для полидисперсных аэрозолей необходимо располагать сведениями о распределении массы или общего числа частиц по их размерам, доли частиц отдельных размеров, среднем размере частиц и т.д.
Дисперсность пыли задается рядом фракций (фракционным составом), т.е. долями общей массы аэрозоля, размеры частиц которых находятся в определенном интервале значений, принятых в качестве верхнего и нижнего пределов.
В общем случае размеры частиц промышленных аэрозолей (пыли) формируются под действием множества факторов, влияние каждого из которых не может быть точно учтено. В подобных случаях вступают в действие законы теории вероятности и математической статистики, а, именно: размер частицы (её э квивалентный d э или седиментационный d с диаметры) рассматривается как случайная величина. Тогда дисперсионные свойства пыли удобно описывать вероятностной функцией распределения m (d э) массы частиц аэрозоля по его размерам d э.
Функция m (d) равна выраженному в процентах отношению массы частиц, размер которых меньше или равен определенного размера di, к их общей массе:
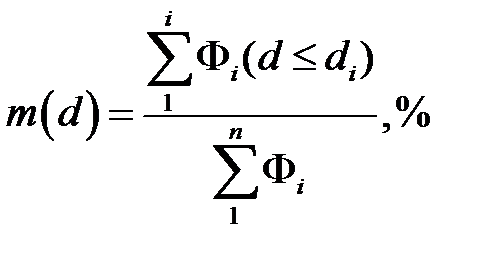 (1.1)
(1.1)
Установлено, что для аэрозольных частиц промышленной пыли и порошкообразных материалов наиболее характерен закон логарифмически нормального распределения (ЛНР), который математически можно выразить в виде:
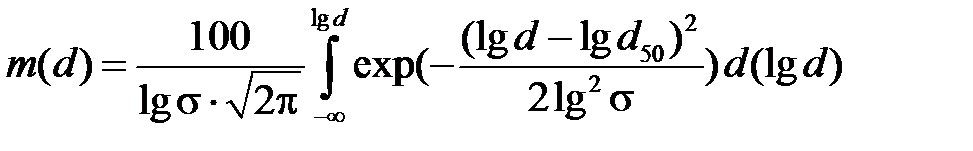 (1.2)
(1.2)
В формуле (1.2) обозначены: d 50 – т.н. медианный диаметр частиц (медиана) пыли, для которой 50% общей массы пыли лежит до этой величины, а 50% массы после этой величины; lg s - стандартное (среднеквадратическое) отклонение логарифмов текущих диаметров частиц d от их среднего значения.
Интеграл, входящий в формулу (1.2), не может быть выражен через элементарные функции. Однако, производя замену переменной (нормирование относительно медианы d 50):
x = (lg d – lg d 50) / lg s, (1.3)
получают табулированную функцию нормального распределения Гаусса (рис. 1, Приложение 2):
 , (1.4)
, (1.4)
для которой существует однозначная связь между функцией F 0(x) и её аргументом x.
| х, (m (d),%) |
| 16,9 |
| (·) 1 |
| d, (lg d) |
| 84,1 |
| (·) 3 |
| (·) 2 |
| 100. F 0 (x), % |
| х |
| -1 |
| -2 |
| Рис. 1 |
| Рис. 2 |
| α |
Для описания ЛНР, в практических целях удобно пользоваться логарифмической вероятностной координатной сеткой (рис. 2, Приложение 3), которая характеризуется тем, что: по оси абсцисс – откладывается lg (d) (для наглядности, на вероятностной координатной сетке проставляются сами значения диаметров частиц d); по оси ординат – откладываются значения величины x, определяемой по формуле (1.3) (на вероятностной координатной сетке проставляются значения функции Ф(x) = m (d), т.е. значения нормальной функции распределения от величины x).
Вычерченный на такой сетке график ЛНР изобразится прямой линией, поскольку зависимость x от lg (d) по формуле (1.3) является линейной. Угловой коэффициент tga этой прямой равен tg a = 1 / lg s, здесь a - угол наклона прямой и положительным направлением оси абсцисс. Таким образом:
– более дисперсный порошкообразный материал (пыль, аэрозоль) обладает большим значение дисперсии s и соответственно меньшим углом наклона прямой a;
– чем ближе к вертикале линия распределения на логарифмически вероятностной координатной сетке, тем порошкообразный материал (пыль, аэрозоль) менее дисперсен и более однороден по своим размерам;
– более измельченному материалу соответствует меньший медианный диаметр d 50 частицы и более высокое расположение на логарифмически вероятностной координатной сетке.
Стандартное (среднеквадратическое) отклонение логарифмов диаметров частиц из формулы (1.3) можно определить как:
lg s = (lg d – lg d 50) / x,
тогда при x = ± 1:
lg s = ± (lg d – lg d50),
или, для x = +1 из табулированной функции нормального распределения Гаусса (Приложение 2) следует, что F 0 = 0,841, или
lg s = lg d 84,1 – lg d 50 = lg (d 84,1 / d 50). (1.5а)
Аналогично, для x = –1 следует, что F 0 = 0,159 (Приложение 2), или
lg s = lg d 50 – lg d 15,9 = lg (d 50 / d 15,9). (1.5б)
Отсюда видно, что среднеквадратическое отклонение можно определить:
lg s = lg (d 84,1 / d 50) = lg (d 50 / d 15,9),
или
s = d 84,1 / d 50 = d 50 / d 15,9 (1.6)
Из вышеизложенного следует, что для порошкообразных материалов (пылей) и аэрозолей, подчиняющихся ЛНР, достаточно указать два параметра для получения представления о дисперсном (фракционном) составе, а именно:
во-первых, значение медианного диаметра d50;
во-вторых, значение среднего логарифмического отклонения s, т.е. параметра, который характеризует наклон прямой ЛНР на логарифмически вероятностной координатной сетке.
Все эти рассуждения, применяются в основном для твердых порошкообразных материалов (аэрозолей, пыли). ГОСТ 12.2.043–80 подразделяет все пыли на пять групп в зависимости от дисперсности:
I – очень крупнодисперсная пыль (уголь);
II – крупнодисперсная пыль (например, мелкий песок для строительных работ по ГОСТ 8736 – 77);
III – среднедисперсная пыль (например, цемент)
IV – мелкодисперсная пыль (например, взвешенная атмосферная пыль);
V – очень мелкодисперсная пыль.
Несмотря на то, что ГОСТ 12.2.043-80 не действует на территории РФ,
данная классификация используется при выборе пылеулавливающего
оборудования.
Определение дисперсного состава пыли древесной
Как правило, состав пыли содержит частицы различных размеров (полидисперсные). Таким образом, для таких аэрозолей необходимо располагать сведениями о распределении массы или общего числа частиц по их размерам, доли частиц отдельных размеров, среднем размере частиц и т.д.
Дисперсность пыли задается рядом фракций (фракционным составом), т.е. долями общей массы аэрозоля, размеры частиц которых находятся в определенном интервале значений, принятых в качестве верхнего и нижнего пределов (таблица 1).
Таблица 1.
| Размеры частицы пыли d э на границах фракций, мкм | < 5 | 5-10 | 10-20 | 20-40 | 40-60 | 60-100 | > 100 |
| Распределение общей массы частиц пыли по фракциям, Ф i, % | 1,2 | 11,5 | 15,5 | 20,8 | |||
| Массовая доля частиц пыли для фракций менее заданного размера, m (d), % | 2,2 | 13,7 | 29,2 |
На логарифмическую вероятностную сетку наносим точки, соответствующие распределению общей массы частиц пыли по фракциям и массовой доля частиц пыли для фракций менее заданного размера. Полученные точки соединяем прямой линией (Приложение 1).
На логарифмической вероятностной сетке, на оси ординат выделяем точки, соответствующие массовой доли пыли 15,9%, 50% и 84,1%, для которых на прямой распределения находим соответствующие им значения диметров частиц пыли d 15,9, d 50 и d 84,1 (Приложение 1). Получаем:
d 50 = 45 мкм,
d 15,9 = 22 мкм,
d 84,1=100 мкм.
По формулам, находим среднеквадратическое отклонение диаметров частиц: s' = d 50 / d 15,9; s" = d 84,1 / d 50 .

Теоретически, значения s' и s" должны быть s' ≈ s". Однако на практике, как правило, эти значения отличаются, поэтому среднеквадратическое отклонение диаметров частиц рассчитывают как их среднее арифметическое:
s = (s' + s") /2
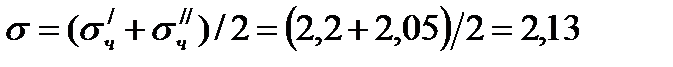
Для определения классификационной группы заданной пыли на номограмму наносят точки, соответствующие содержанию каждой фракции пыли. Полученные точки соединяют линией. Положение образованной прямой или ломаной линии в той или иной зоне номограммы, обозначенной римскими цифрами I – V, указывает на принадлежность заданной пыли к соответствующей классификационной группе по ГОСТ 12.2.034 – 80 (Приложение 3). Данная пыль относится к III группе (средне-дисперсная пыль).