Лабораторная работа №1
Изучение основных методов классификации с использованием приложения “Orange”.
Цель и задача работы
Ознакомиться и получить навыки работы с GUI интерфейсом приложения Orange Data Mining.
Осуществить классификацию тестовых данных используя разные алгоритмы. Научиться сравнивать результаты работы алгоритмов классификации и выбирать наиболее подходящий.
Теоретические положения
Понятие классификации
Классификация — отнесение входного вектора (объекта, события, наблюдения) к одному из заранее известных классов. Главное отличие классификации от кластеризации состоит в том, что перечень групп четко задан и в процессе работы алгоритма необходимо отнести новый набор входных данных к известному классу.
В ряде случаев данные, с которыми работают алгоритмы классификации, имеют следующие особенности:
● большое количество записей (как правило сотни тысяч и миллионы);
● записи содержат большое количество числовых и категорийных атрибутов (полей).
Все атрибуты записей делятся на числовые и категорийные. Числовые атрибуты могут быть упорядочены в пространстве, соответственно категорийные не могут быть упорядочены. Например, атрибуты “широта” и “долгота” – числовые, а “образование” или “цвет” – категорийные.
Классификация является наиболее простой и одновременно наиболее часто решаемой задачей Data Mining. Ввиду распространенности задач классификации необходимо четкое понимания сути этого понятия.
Приведем несколько определений.
Классификация - системное распределение изучаемых предметов, явлений, процессов по родам, видам, типам, по каким-либо существенным признакам для удобства их исследования; группировка исходных понятий и расположение их в определенном порядке, отражающем степень этого сходства.
Классификация - упорядоченное по некоторому принципу множество объектов, которые имеют сходные классификационные признаки (одно или несколько свойств), выбранных для определения сходства или различия между этими объектами.
Классификация требует соблюдения следующих правил:
● в каждом акте деления необходимо применять только одно основание;
● деление должно быть соразмерным, т.е. общий объем видовых понятий должен равняться объему делимого родового понятия;
● члены деления должны взаимно исключать друг друга, их объемы не должны перекрещиваться;
● деление должно быть последовательным.
Различают:
● вспомогательную (искусственную) классификацию, которая производится по внешнему признаку и служит для придания множеству предметов (процессов, явлений) нужного порядка;
● естественную классификацию, которая производится по существенным признакам, характеризующим внутреннюю общность предметов и явлений. Она является результатом и важным средством научного исследования, т.к. предполагает и закрепляет результаты изучения закономерностей классифицируемых объектов.
В зависимости от выбранных признаков, их сочетания и процедуры деления понятий классификация может быть:
1. простой - деление родового понятия только по признаку и только один раз до раскрытия всех видов. Примером такой классификации является дихотомия, при которой членами деления бывают только два понятия, каждое из которых является противоречащим другому (т.е. соблюдается принцип: "А и не А");
2. сложной - применяется для деления одного понятия по разным основаниям и синтеза таких простых делений в единое целое. Примером такой классификации является периодическая система химических элементов.
Под классификацией будем понимать отнесение объектов (наблюдений, событий) к одному из заранее известных классов.
Классификация - это закономерность, позволяющая делать вывод относительно определения характеристик конкретной группы. Таким образом, для проведения классификации должны присутствовать признаки, характеризующие группу, к которой принадлежит то или иное событие или объект (обычно при этом на основании анализа уже классифицированных событий формулируются некие правила).
Классификация относится к стратегии обучения с учителем (supervised learning), которое также именуют контролируемым или управляемым обучением.
Задачей классификации часто называют предсказание категориальной зависимой переменной (т.е. зависимой переменной, являющейся категорией) на основе выборки непрерывных и/или категориальных переменных.
Например, можно предсказать, кто из клиентов фирмы является потенциальным покупателем определенного товара, а кто - нет, кто воспользуется услугой фирмы, а кто - нет, и т.д. Этот тип задач относится к задачам бинарной классификации, в них зависимая переменная может принимать только два значения (например, да или нет, 0 или 1).
Другой вариант классификации возникает, если зависимая переменная может принимать значения из некоторого множества предопределенных классов. Например, когда необходимо предсказать, какую марку автомобиля захочет купить клиент. В этих случаях рассматривается множество классов для зависимой переменной.
Классификация может быть одномерной (по одному признаку) и многомерной (по двум и более признакам).
Многомерная классификация была разработана биологами при решении проблем дискриминации для классифицирования организмов. Одной из первых работ, посвященных этому направлению, считают работу Р. Фишера (1930 г.), в которой организмы разделялись на подвиды в зависимости от результатов измерений их физических параметров. Биология была и остается наиболее востребованной и удобной средой для разработки многомерных методов классификации.
Рассмотрим задачу классификации на простом примере. Допустим, имеется база данных о клиентах туристического агентства с информацией о возрасте и доходе за месяц. Есть рекламный материал двух видов: более дорогой и комфортный отдых и более дешевый, молодежный отдых. Соответственно, определены два класса клиентов: класс 1 и класс 2.
Процесс классификации
Цель процесса классификации состоит в том, чтобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута. Процесс классификации заключается в разбиении множества объектов на классы по определенному критерию.
Классификатором называется некая сущность, определяющая, какому из предопределенных классов принадлежит объект по вектору признаков.
Для проведения классификации с помощью математических методов необходимо иметь формальное описание объекта, которым можно оперировать, используя математический аппарат классификации. Таким описанием в нашем случае выступает база данных. Каждый объект (запись базы данных) несет информацию о некотором свойстве объекта.
Набор исходных данных (или выборку данных) разбивают на два множества: обучающее и тестовое.
Обучающее множество (training set) - множество, которое включает данные, использующиеся для обучения (конструирования) модели.
Такое множество содержит входные и выходные (целевые) значения примеров. Выходные значения предназначены для обучения модели.
Тестовое (test set) множество также содержит входные и выходные значения примеров. Здесь выходные значения используются для проверки работоспособности модели.
Процесс классификации состоит из двух этапов: конструирования модели и ее использования.
1. Конструирование модели: описание множества предопределенных классов.
a. Каждый пример набора данных относится к одному предопределенному классу.
b. На этом этапе используется обучающее множество, на нем происходит конструирование модели.
c. Полученная модель представлена классификационными правилами, деревом решений или математической формулой.
2. Использование модели: классификация новых или неизвестных значений.
a. Оценка правильности (точности) модели.
i. Известные значения из тестового примера сравниваются с результатами использования полученной модели.
ii. Уровень точности - процент правильно классифицированных примеров в тестовом множестве.
iii. Тестовое множество, т.е. множество, на котором тестируется построенная модель, не должно зависеть от обучающего множества.
b. Если точность модели допустима, возможно использование модели для классификации новых примеров, класс которых неизвестен.
Алгоритмы классификации
Дерево решений
Дерево принятия решений (также может называться деревом классификации или регрессионным деревом) — средство поддержки принятия решений, использующееся в статистике и анализе данных для прогнозных моделей. Структура дерева представляет собой «листья» и «ветки». На ребрах («ветках») дерева решения записаны атрибуты, от которых зависит целевая функция, в «листьях» записаны значения целевой функции, а в остальных узлах — атрибуты, по которым различаются случаи.
Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Подобные деревья решений широко используются в интеллектуальном анализе данных. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких переменных на входе.
Каждый лист представляет собой значение целевой переменной, измененной в ходе движения от корня по листу. Каждый внутренний узел соответствует одной из входных переменных. Дерево может быть также «изучено» разделением исходных наборов переменных на подмножества, основанные на тестировании значений атрибутов. Это процесс, который повторяется на каждом из полученных подмножеств. Рекурсия завершается тогда, когда подмножество в узле имеет те же значения целевой переменной, таким образом, оно не добавляет ценности для предсказаний. Процесс, идущий «сверху вниз», индукция деревьев решений (TDIDT), является примером поглощающего «жадного» алгоритма, и на сегодняшний день является наиболее распространенной стратегией деревьев решений для данных, но это не единственная возможная стратегия. В интеллектуальном анализе данных, деревья решений могут быть использованы в качестве математических и вычислительных методов, чтобы помочь описать, классифицировать и обобщить набор данных, которые могут быть записаны следующим образом:
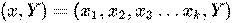
Зависимая переменная Y является целевой переменной, которую необходимо проанализировать, классифицировать и обобщить. Вектор x состоит из входных переменных x1, x2, x3 и т. д., которые используются для выполнения этой задачи.
Наивный байесовский классификатор
Наи́вный ба́йесовский классифика́тор (Naïve Bayes Classifier) — простой вероятностный классификатор, основанный на применении Теоремы Байеса со строгими (наивными) предположениями о независимости.
Теорема Байеса может быть выражена формулой.
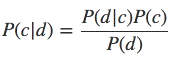
где,
● P (c|d)— вероятность что объект d принадлежит классу c, именно её нам надо рассчитать;
● P (d|c) — вероятность встретить объект d среди всех объектов класса c;
● P (c) — безусловная вероятность встретить объект класса c в корпусе объектов;
● P (d) — безусловная вероятность документа d в корпусе объектов.
Её смысл на обывательском уровне можно выразить следующим образом. Теорема Байеса позволяет переставить местами причину и следствие. Зная с какой вероятностью причина приводит к некоему событию, эта теорема позволяет рассчитать вероятность того что именно эта причина привела к наблюдаемому событию.
В зависимости от точной природы вероятностной модели, наивные байесовские классификаторы могут обучаться очень эффективно. Во многих практических приложениях для оценки параметров для наивных байесовых моделей используют метод максимального правдоподобия; другими словами, можно работать с наивной байесовской моделью, не веря в байесовскую вероятность и не используя байесовские методы.
Несмотря на наивный вид и, несомненно, очень упрощенные условия, наивные байесовские классификаторы часто работают намного лучше во многих сложных жизненных ситуациях.
Достоинством наивного байесовского классификатора является малое количество данных для обучения, необходимых для оценки параметров, требуемых для классификации.
Одним из примеров использования данного классификатора можно считать отнесение электронных писем к спаму на основе частоты встречающихся слов (характерных для спама: купи, скидка, специальное предложение, подарок и т.д.)
Логистическая регрессия
Логистическая регрессия или логит-регрессия (англ. logit model) — это статистическая модель, используемая для предсказания вероятности возникновения некоторого события путём подгонки данных к логистической кривой.
Логистическая регрессия применяется для предсказания вероятности возникновения некоторого события по значениям множества признаков. Для этого вводится так называемая зависимая переменная y, принимающая лишь одно из двух значений — как правило, это числа 0 (событие не произошло) и 1 (событие произошло), и множество независимых переменных (также называемых признаками, предикторами или регрессорами) — вещественных x1, x2, … xn, на основе значений которых требуется вычислить вероятность принятия того или иного значения зависимой переменной.
Делается предположение о том, что вероятность наступления события y= 1равна:
где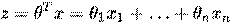 
, x и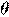 
— векторы-столбцы значений независимых переменных x1, x2, … xn и параметров (коэффициентов регрессии) — вещественных чисел 
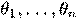, соответственно, а 
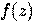— так называемая логистическая функция (иногда также называемая сигмоидом или логит-функцией):
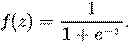
Так как y принимает лишь значения 0 и 1, то вероятность первого возможного значения равна:
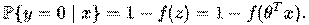
Для краткости функцию распределения y при заданном x можно записать в таком виде:
В итоге объект x можно отнести к классу y =1, если предсказанная моделью вероятность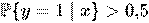 
, и к классу y =0 в противном случае.
Метод опорных векторов
Метод опорных векторов (англ. SVM, support vector machine) — набор схожих алгоритмов обучения с учителем, использующихся для задач классификации и регрессионного анализа. Принадлежит семейству линейных классификаторов и может также рассматриваться как специальный случай регуляризации по Тихонову. Особым свойством метода опорных векторов является непрерывное уменьшение эмпирической ошибки классификации и увеличение зазора, поэтому метод также известен как метод классификатора с максимальным зазором.
Основная идея метода — перевод исходных векторов в пространство более высокой размерности и поиск разделяющей гиперплоскости с максимальным зазором в этом пространстве. Две параллельных гиперплоскости строятся по обеим сторонам гиперплоскости, разделяющей классы. Разделяющей гиперплоскостью будет гиперплоскость, максимизирующая расстояние до двух параллельных гиперплоскостей. Алгоритм работает в предположении, что чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше будет средняя ошибка классификатора.
Часто в алгоритмах машинного обучения возникает необходимость классифицировать данные. Каждый объект данных представляется как вектор (точка) в p -мерном пространстве (упорядоченный набор p чисел). Каждая из этих точек принадлежит только одному из двух классов. Вопрос состоит в том, можно ли разделить точки гиперплоскостью размерности (p −1). Это - типичный случай линейной разделимости. Искомых гиперплоскостей может быть много, поэтому полагают, что максимизация зазора между классами способствует более уверенной классификации. То есть, можно ли найти такую гиперплоскость, чтобы расстояние от неё до ближайшей точки было максимальным. Это эквивалентно тому, что расстояние между двумя ближайшими точками, лежащими по разные стороны гиперплоскости, максимально. Если такая гиперплоскость существует, она называется оптимальной разделяющей гиперплоскостью, а соответствующий ей линейный классификатор называется оптимально разделяющим классификатором.
Ближайший сосед
Метод ближайших соседей — простейший метрический классификатор, основанный на оценивании сходства объектов. Классифицируемый объект относится к тому классу, которому принадлежат ближайшие к нему объекты обучающей выборки.
Человек, сталкиваясь с новой задачей, использует свой жизненный опыт, вспоминает аналогичные ситуации, которые когда-то с ним происходили. О свойствах нового объекта мы судим, полагаясь на похожие знакомые наблюдения. Например, встретив иностранца на улице, мы можем догадаться о его происхождении по речи, жестам и внешности. Для этого необходимо вспомнить наиболее похожего человека на него, происхождение которого известно.
Так, подобно приведенному выше примеру, сходство объектов лежит в основе алгоритма k-ближайших соседей (k-nearest neighbor algorithm, KNN). Алгоритм способен выделить среди всех наблюдений k известных объектов (k-ближайших соседей), похожих на новый неизвестный ранее объект. На основе классов ближайших соседей выносится решение касательно нового объекта. Важной задачей данного алгоритма является подбор коэффициента k – количество записей, которые будут считаться близкими.
Случайный лес
Random forest (с англ. — «случайный лес») — алгоритм машинного обучения, предложенный Лео Брейманом и Адель Катлер, заключающийся в использовании комитета (ансамбля) решающих деревьев. Алгоритм сочетает в себе две основные идеи: метод бэггинга Бреймана, и метод случайных подпространств, предложенный Tin Kam Ho. Алгоритм применяется для задач классификации, регрессии и кластеризации.
Пусть обучающая выборка состоит из N примеров, размерность пространства признаков равна M, и задан параметр m (в задачах классификации обычно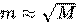 
).
Все деревья комитета строятся независимо друг от друга по следующей процедуре:
1. Сгенерируем случайную подвыборку с повторением размером N из обучающей выборки. (Таким образом, некоторые примеры попадут в неё несколько раз, а в среднем N *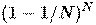 
, т.е. примерно N /e примеров не войдут в неё вообще)
2. Построим решающее дерево, классифицирующее примеры данной подвыборки, причём в ходе создания очередного узла дерева будем выбирать признак, на основе которого производится разбиение, не из всех M признаков, а лишь из m случайно выбранных. Выбор наилучшего из этих m признаков может осуществляться различными способами. В оригинальном коде Бреймана используется критерий Джини, применяющийся также в алгоритме построения решающих деревьев CART. В некоторых реализациях алгоритма вместо него используется критерий прироста информации.
3. Дерево строится до полного исчерпания подвыборки и не подвергается процедуре прунинга (англ. pruning — отсечение ветвей) (в отличие от решающих деревьев, построенных по таким алгоритмам, как CART или C4.5).
Классификация объектов проводится путём голосования: каждое дерево комитета относит классифицируемый объект к одному из классов, и побеждает класс, за который проголосовало наибольшее число деревьев.
Оптимальное число деревьев подбирается таким образом, чтобы минимизировать ошибку классификатора на тестовой выборке. В случае её отсутствия, минимизируется оценка ошибки out-of-bag: доля примеров обучающей выборки, неправильно классифицируемых комитетом, если не учитывать голоса деревьев на примерах, входящих в их собственную обучающую подвыборку.
Точность классификации: оценка уровня ошибок
Оценка точности классификации может проводиться при помощи кросс-проверки. Кросс-проверка (Cross-validation) - это процедура оценки точности классификации на данных из тестового множества, которое также называют кросс-проверочным множеством. Точность классификации тестового множества сравнивается с точностью классификации обучающего множества. Если классификация тестового множества дает приблизительно такие же результаты по точности, как и классификация обучающего множества, считается, что данная модель прошла кросс-проверку.
Разделение на обучающее и тестовое множества осуществляется путем деления выборки в определенной пропорции, например обучающее множество - две трети данных и тестовое - одна треть данных. Этот способ следует использовать для выборок с большим количеством примеров. Если же выборка имеет малые объемы, рекомендуется применять специальные методы, при использовании которых обучающая и тестовая выборки могут частично пересекаться.