Точки пространства обозначают прописными буквами латинского алфавита: А,В,С,Д,...., или арабскими цифрами 1,2,3,4,...;
¨ прямые и кривые линии пространства - строчными буквами латинского алфавита: а,b,c,d,...m,n,l;
¨ плоскости и поверхности пространства - прописными буквами греческого алфавита: G (гамма), q (тета), L(ламбда), S (сигма), Ф (фи), Y (пси), W (омега)....;
¨ плоскость (поле) проекции - П (пи);
¨ углы - греческими буквами a,b,g,d,....
Символы, обозначающие отношение между геометрическими элементами, фигурами:
º - совпадение двух геометрических элементов,
@ - конгруэнтность фигур,
~ - фигуры подобные
Ì - знак включения, содержания,
Î - принадлежность элемента,
|| - параллельность,
Ç - пересечение,
¸ - перекрещивание,
Ç - касание,
È - объединение (соединение),
= - результат геометрической операции,
Þ - если..... то,
L - и.
Пример записи в символах. Если прямая l параллельна m и m принадлежит плоскости S, то прямая l параллельна плоскости S: l || m L m Ì S Þ l || S
I.3. Метод проецирования
Все задачи начертательная геометрия решает своим, присущим только ей методом - методом проецирования. С помощью этого метода устанавливается связь между оригиналом и его изображением. Он позволяет составить алгоритм графических операций, необходимых для построения изображения и чтения чертежа, а также для решения позиционных и метрических задач.
В аппарат проецирования входят следующие элементы: плоскость проекций - П¢, которую иногда называют картинной плоскостью или носителем проекций; центр проекций (полюс проекций) - S; объект проецирования (фигура, представленная геометрическими элементами).
| Рис. 1.1 |
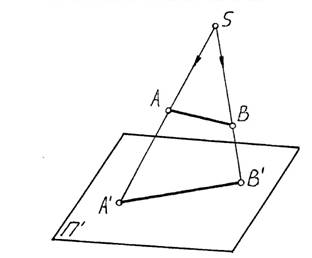 На рис. 1.1. представлен пример проецирования отрезка прямой [АВ] на плоскость проекций П¢. Операция проецирования состоит из трех этапов:
На рис. 1.1. представлен пример проецирования отрезка прямой [АВ] на плоскость проекций П¢. Операция проецирования состоит из трех этапов:
1- соединение оригинала с центром проецирования: SÈA = [SA) - луч с началом в точке S (проецирующий луч), SÈB = [SB);
2- пересечение проецирующих лучей с плоскостью проекций: [SA) Ç П¢= А¢; [SB) Ç П¢= B¢, где А¢ и B¢ являются проекциями точек А и В;
3- соединение проекций точек А¢ и B¢: А¢ÈB¢ = [А¢B¢] - проекция отрезка [АВ] на плоскость П¢.
Виды проецирования
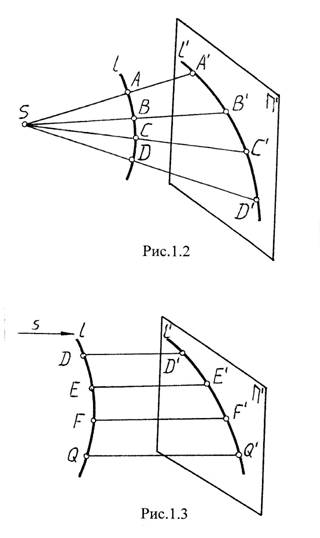 Рис.1.2
Рис.1.3
Рис.1.2
Рис.1.3
|
В зависимости от расположения центра проецирования S и плоскости проекций П¢ проецирование может быть: центральным (коническим), когда центр проецирования расположен на конечном расстоянии от плоскости проекций (рис.1.1., рис. 1,2.), параллельным (цилиндрическим), когда центр проецирования удален от плоскости проекций в бесконечность. При параллельном проецировании задается направление проецирования s. Полученное таким образом изображение называется параллельной проекцией.
На рис. 1.3. показано построение параллельной проекции кривой линии l. Проецирующие лучи в данном случае будут параллельны и, следовательно, составляют с плоскостью проекций П¢ один и тот же угол. Если этот угол не равен 90°, то параллельное проецирование называется косоугольным. В случае, когда проецирующие лучи направлены перпендикулярно плоскости проекций, т.е. когда s^П¢, параллельное проецирование называется прямоугольным или ортогональным.
Из сказанного очевидно, что параллельное проецирование является частным случаем центрального проецирования, а прямоугольное в свою очередь, частным случаем параллельного проецирования.
Основные свойства параллельного
Проецирования
1. Проекция точки есть точка. Это следует из самого. процесса (операций) проецирования.
2. Проекция прямой в общем случае есть прямая (рис. 1.4.). Для построения ортогональной проекции прямой l (A,B) проводятся два проецирующих луча а и b параллельно направлению проецирования s. Они параллельны между собой и определяют плоскость å, которая пересекается с плоскостью проекций П¢ по прямой l¢. В символах: åÇП¢ = l¢.
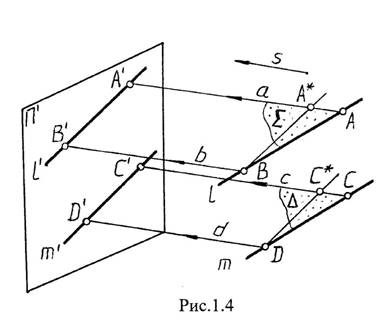 Рис.1.4
Рис.1.4
|
3. Свойство параллельности. Если прямые в пространстве параллельны, то параллельны и их проекции. (рис. 1.4.). На рисунке видим, что прямая l с лучами а и b и прямая m с лучами c и d образуют соответственно две параллельные плоскости å и D. (å||D) ÇП¢Þl¢||m¢.
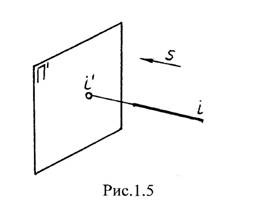 Рис.1.5
Рис.1.5
|
4. Если прямая совпадает с направлением проецирования, то её проекция вырождается в точку и такая прямая называется проецирующей (рис. 1.5.).
5. Плоскость в общем случае проецируется полем множества точек. Но если плоскость совпадает с направлением проецирования, то её проекция вырождается в прямую линию, как это видно по рис. 1.4. на примере плоскости å или D.
6. Отношение длин отрезков двух параллельных прямых равно отношению длин их проекций (см. рис. 1.4.). Треугольник АА*В подобен треугольнику СС*D, как треугольник со взаимно параллельными сторонами, поэтому

 АВ А*В А*В = А¢В¢, и АВ А¢В¢
АВ А*В А*В = А¢В¢, и АВ А¢В¢

 СD C*D C*D = C¢D¢ следовательно CD C¢D¢.
СD C*D C*D = C¢D¢ следовательно CD C¢D¢.
7. Свойство принадлежности. Если точка лежит на прямой, то ее проекция принадлежит проекции данной прямой, что видно на том же рис. 1.4.
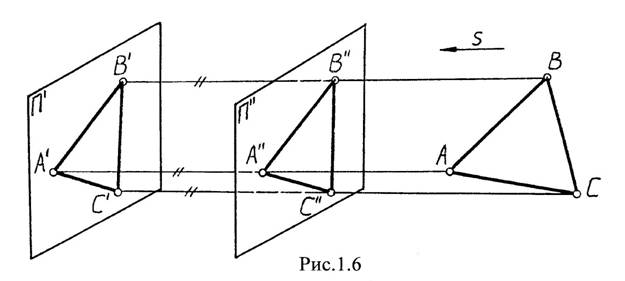
8. При параллельном переносе плоскости проекций проекция фигуры не меняется (рис. 1.6.).
А¢А¢¢=В¢В¢¢=С¢С¢¢ и параллельны, следовательно, А¢В¢В¢¢А¢¢, В¢С¢С¢¢В¢¢ и С¢А¢А¢¢С¢¢ являются параллелограммами, у которых противоположные стороны, как известно, равны. Поэтому А¢В¢¢=А¢¢В¢¢,В¢С¢=В¢¢С¢¢,С¢А¢=С¢¢А¢¢т.е. DА¢В¢С¢=DА¢¢В¢¢С¢¢.
 1.6. Способы дополнения
1.6. Способы дополнения