Разверткой многогранной поверхности называется совокупность конгруэнтных ее граням многоугольников, расположенных в одной плоскости, если указано соответствие сторонам и вершинам многоугольников ребер и вершин данной многогранной поверхности.
Из этого определения следует, что, имея многогранную поверхность, мы можем всегда построить ее развертку. Для этого достаточно построить в какой-либо плоскости совокупность многоугольников, конгруэнтных граням многогранника.
Рассмотрим построение точных разверток наиболее распространенных многогранных поверхностей - поверхностей пирамид и призм.
Так как у пирамиды боковые грани-треугольники, то построение ее развертки сводится к построению натуральных величин этих треугольников, для чего необходимо найти натуральные величины всех ребер пирамиды.
| Рис.13.1 |
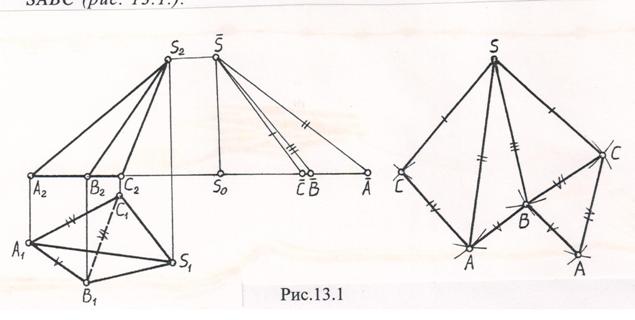Пример. Построить развертку поверхности пирамиды SABC (рис. 13.1.).
Основание АВС пирамиды лежит в горизонтальной плоскости уровня. Поэтому его стороны на П1 проецируются в натуральную величину. Для определения натуральных величин боковых ребер воспользуемся способом прямоугольного треугольника. Так как разность высот концов всех боковых ребер равны, то построим прямоугольные треугольники с общим катетом `SS0. Вторые катеты этих треугольников равны длинам горизонтальных проекций этих ребер. Построение натуральных величин боковых ребер для удобства вынесено на свободное поле чертежа. Совокупность треугольников `SS0`A, `SS0`B, `SS0`C с общим катетом `SS0 называется диаграммой натуральных величин.
Построение развертки поверхности пирамиды ясно из приведенного чертежа, на котором конгруэнтные отрезки обозначены одинаковыми значками.
К развертке боковой поверхности пирамиды пристраиваем ее основание.
Построение развертки поверхности призмы выполняется тремя способами:
1) способ треугольников (треангуляции),
2) способ нормальных сечений,
3) способ раскатки.
Способ тренгуляции является наиболее универсальным. Он пригоден для построения точных разверток любых многогранных поверхностей, а также для построения приближенных и условных разверток линейчатых поверхностей.
По способу триангуляции развертка призмы строится в такой последовательности:
¨ в каждой грани призмы проводится диагональ, которая разбивает ее на два треугольника;
¨ определяются натуральные величины сторон этих треугольников;
¨ на плоскости строятся последовательно треугольники, конгруэнтные данным.
Пример. Построить развертку боковой поверхности трехгранной призмы АВСА¢В¢С¢ (рис. 13.2).
В каждой из боковых граней призмы проводим диагональ и построим на свободном поле чертежа диаграммы натуральных величин боковых ребер `А`А¢=`В`В¢=`С`С¢ и построенных диагоналей `А`В¢,`В`С¢,`С`А¢. Основания призмы 
параллельны горизонтальной плоскости проекций,
| Рис.13.2 |
поэтому они проецируются на П1 в натуральную величину.
Имея натуральные величины ребер призмы и трех диагоналей, строим развертку боковой поверхности призмы как совокупности треугольников, определяемых своими сторонами. На рисунке 13.2 конгруэнтные отрезки обозначены одинаковыми значками, что позволяет проследить алгоритм построения развертки.
Способ нормальных сечений применяется для построения разверток призматических поверхностей, если их боковые ребра являются прямыми уровня.
Развертка поверхности призмы способом нормальных сечений выполняется в такой последовательности:
¨ призма пересекается плоскостью S, перпендикулярной ее боковым ребрам;
¨ определяются натуральные величины сторон полученного в сечении многоугольника;
¨ стороны многоугольника развертываются в одну прямую;
¨ на перпендикулярах, проведенных к этой прямой, в точках, соответственных вершинам многоугольника, откладываются натуральные величины соответствующих отрезков ребер;
¨ концы ребер последовательно соединяются отрезками прямых;
¨ к построенной развертке боковой поверхности призмы пристраиваются многоугольники, равные натуральным величинам оснований призмы.
| Рис.13.3 |
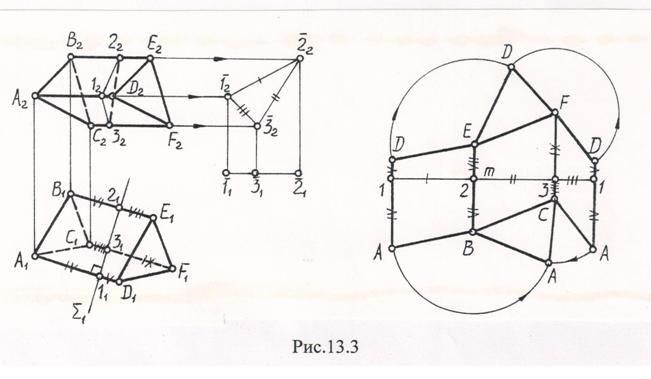Пример. Построить развертку трехгранной призмы АВСDEF (рис. 13.3).
Боковые ребра призмы являются горизонталями. Поэтому на плоскость П1 они проецируются в натуральную величину.
Построим сечение 123 призмы горизонтально проецирующей плоскостью S, перпендикулярной ее боковым ребрам. Способом плоскопараллельного движения относительно П1 определяем натуральную величину треугольника 123 и, значит, натуральные величины его сторон.
Стороны многоугольника 1231 “вытягиваем” в прямую линию m и через отмеченные вершины проводим прямые, перпендикулярные прямой m. На этих перпендикулярах по обе стороны прямой m откладываем натуральные величины отрезков боковых ребер призмы, равные их горизонтальным проекциям: [A1]=[A111], [1D]=[11D1],.......
Концы ребер последовательно соединяем отрезками прямых. Полученный многоугольник АВСАDFED представляет собой развертку боковой поверхности призмы, к которой пристраиваем треугольники ABC и DEF, равные натуральным величинам ее оснований.
Способ раскатки применяется для построения разверток призматических поверхностей, если их боковые ребра и плоскости оснований являются соответственно прямыми и плоскостями уровня.
Сущность способа раскатки состоит в том, что грани призмы последовательными вращениями вокруг одного из боковых ребер совмещаются с какой-либо плоскостью. Получающаяся при этом фигура является разверткой боковой поверхности призмы.
| Рис.13.4 |
Пример. Построить развертку боковой поверхности трехгранной призмы АВСDEF (рис. 13.4).
Боковые ребра призмы являются фронталями, а ее основания - горизонтальными плоскостями уровня, что позволяет строить развертку поверхности призмы способом раскатки.
Примем за ось вращения ребро CF и вращением вокруг него совместим грань CFDA с фронтальной плоскостью F, проходящей через ребро CF. При этом вершины А и D вращаются во фронтально проецирующих плоскостях S1'A, S4'D1, перпендикулярных оси вращения СF. Поэтому совмещенные положения `А2,`D вершин A,D принадлежат вырожденным проекциям S12, S24 плоскостей S1,S4 и отстоят от точек C,F на расстоянии [C2`А2]=[C1A1]=[F2`D2]=[F1D1].
Далее последовательными вращениями вокруг СF совмещаем с плоскостью F грани ABED и BCFE.