НАДЕЖНОСТЬ ОСНОВНОЙ СИСТЕМЫ
Основные системы (ОС) являются простейшими техническими системами, в которых отказ одного элемента приводит к отказу всей системы.
Работоспособность основной системы обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии.

Поскольку события, заключающиеся в работоспособности элементов системы, являются независимыми, то
| вероятность безотказной работы (ВБР) ОС: | 
|
| вероятность отказа (ВО) ОС: | 
|
При идентичных элементах ОС P1(t) = … = Pn(t) = P(t):
| ВБР: | Pс(t) = P n(t); | ВО: | Qс(t) = 1 - P n(t). |
Поскольку на участке нормальной эксплуатации наработку до отказа можно описать экспоненциальным распределением каждого элемента
Pi(t) = exp(-  i · t),
i · t),
где  i = const, то
i = const, то
| ВБР ОС: | 
|
Используя уравнение связи показателей безотказности, выражающее ВБР любого объекта, в том числе и системы

и полагая

получаем, что интенсивность отказов (ИО) ОС равна сумме ИО элементов:

В общем случае, для любого распределения наработки ИО системы равна:

Для n идентичных элементов  1(t) = … =
1(t) = … =  n(t) =
n(t) =  (t):
(t):

При экспоненциальном распределении наработки до отказа каждого из n элементов ОС Pi(t) = exp(-  i · t), где
i · t), где  i = const показатели безотказности ОС определяются:
i = const показатели безотказности ОС определяются:
Неидентичные элементы
 1 = … = 1 = … =  n = n = 
| Идентичные элементы
 1 = … = 1 = … =  n = n = 
| |
| ВБР: | 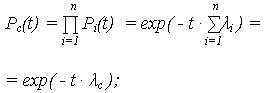
| 
|
| ВО: | 
| 
|
| ИО: | 
| 
|
| МО наработки до отказа: | 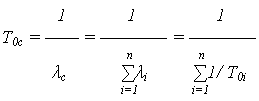
| 
|
Выражения для МО наработки до отказа получены из формулы:

| ПРО: | fс(t) = - d Pс(t)/ dt =  с exp(- t · с exp(- t ·  с); с);
| fс(t) = n ·  · exp(- n · t · · exp(- n · t ·  ). ).
|
Таким образом, при экспоненциальной наработке до отказа каждого из n элементов, распределение наработки до отказа ОС также подчиняется экспоненциальному распределению.
Для ОС надежность меньше надежности каждого из элементов. С увеличением числа элементов надежность ОС уменьшается.
Например, при n = 1000, Pi(t) = 0,99, Pс(t) < 10 - 4 и средняя наработка до отказа системы в 1000 раз меньше средней наработки каждого из элементов.
Распределение норм надежности основной системы по элементам.
Рассмотренные модели позволяют определить показатели безотказности ОС по известным показателям надежности элементов – так решается задача при завершении технического проекта, после испытаний опытных образцов системы и составляющих элементов.
Иначе: значения Pi(t) i –х элементов хорошо известны и лишь уточняется значение Pс(t) и сравнивается с заданным в ТЗ на проект. При этом, если Pс(t) получается меньшей, чем в ТЗ, то принимаются меры по ее повышению (резервирование, использование более надежных элементов и т. п.).
На начальной стадии проектирования в ТЗ указывается лишь ВБР проектируемой системы. При проектировании используются как элементы с известной надежностью, так и элементы, о надежности которых можно судить лишь по их аналогам (прототипам). При этом необходима предварительная оценка надежности элементов, которая, в дальнейшем, уточняется в ходе испытания опытных образцов системы и элементов.
Существуют различные способы распределения норм надежности:
- по принципу равнонадежности элементов;
- с учетом данных об аналогах элементов;
- с учетом перспектив совершенствования элементов.
Выбор того или иного способа зависит от имеющейся информации о проектируемой системе.
1. Распределение надежности по принципу равнонадежности элементов:
Задано: по техническому заданию Pс(t); n – число элементов системы.
Распределение наработки до отказа элементов – экспоненциальное.
При идентичных (равнонадежных) элементах ( 1 = … =
1 = … =  i = … =
i = … =  n=
n=  ):
):

интенсивность отказа i –го элемента: ln Pс(t) = - n ·  · t.
· t.
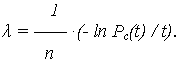
2. Распределение надежности с учетом данных о надежности аналогов.
Задано: по техническому заданию ТЗ Pс(t); n – число элементов системы;
интенсивности отказов аналогов –  аi,
аi,  .
.
Определяется доля отказов системы из-за отказов i –го элемента:
ki =  аi /
аi /  ас,
ас,
где  – ИО системы по данным об аналогах.
– ИО системы по данным об аналогах.
Определяется ИО проектируемой системы: Pс(t) = exp(-  с · t)
с · t)
 с = - ln Pс(t) / t (
с = - ln Pс(t) / t ( с > 0; ln P(t) < 0),
с > 0; ln P(t) < 0),
и ИО составляющих элементов:
 i = ki ·
i = ki ·  с.
с.
3. Распределение надежности с учетом перспектив совершенствования элементов.
Задано: по техническому заданию ТЗ Pс(t); n – число элементов системы;
Изменение ИО аналогов за временной период [19XY по 200Z] годы, аппроксимировано выражением  аi =
аi = 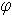 (
( аi, 19 XY),
аi, 19 XY),
где  аi – ИО i –го аналога в 19XY году.
аi – ИО i –го аналога в 19XY году.
По выражению  аi =
аi = 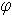 (
( аi, 19 XY) экстраполируется ИО элементов – аналогов к нынешнему году (году проектирования системы), получаются:
аi, 19 XY) экстраполируется ИО элементов – аналогов к нынешнему году (году проектирования системы), получаются:  а1(94),…,
а1(94),…,  аi(94), ….
аi(94), ….
Определяется доля отказов системы из-за отказов i –го элемента:
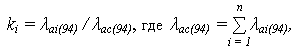
и ИО элементов системы:
 i = ki ·
i = ki ·  с = ki ·(- ln Pс(t) / t).
с = ki ·(- ln Pс(t) / t).
Принципы распределения показателей надежности по 2 и 3 способам отличаются лишь экстраполяцией значений на год проектирования.
Контрольные вопросы и задачи:
- Что такое основная система и в чем состоит условие ее безотказной работы?
- Как определяются показатели безотказности основной системы: ВБР и ИО?
- Как определяются показатели безотказности основной системы: ПРО и МО наработки до отказа?
- Какой закон распределения наработки до отказа будет иметь основная система, если законы распределения наработки до отказа элементов являются экспоненциальными (привести доказательство)?
- В чем заключается необходимость распределения норм надежности между элементами основной системы?
- Какие существуют способы распределения норм надежности между элементами основной системы, и чем они отличаются?
- Структура проектируемой системы представляется основной системой, состоящей из 10 элементов «A», 15 элементов «B», 32 элементов «D» и 8 элементов «F». Интенсивности отказов элементов известны и равны:
 A = 2 · 10 -6 час -1,
A = 2 · 10 -6 час -1,  B = 4 · 10 -6 час -1,
B = 4 · 10 -6 час -1,  D = 2.5 · 10 -6 час -1,
D = 2.5 · 10 -6 час -1,  F = 5 · 10 -6 час -1. Определить среднюю наработку до отказа T0с и ВБР системы за наработки t1 = 100 час, t2 = 1000 час и в интервале указанных наработок? Определить плотность распределения отказов системы при наработке t2 = 1000 час?
F = 5 · 10 -6 час -1. Определить среднюю наработку до отказа T0с и ВБР системы за наработки t1 = 100 час, t2 = 1000 час и в интервале указанных наработок? Определить плотность распределения отказов системы при наработке t2 = 1000 час?
Ответ: T0с = 5 · 10 3 час, P(t1 ) = 0.98, P(t2 ) = 0.819, Pс(t1, t2 ) = 0.836, f(t2 ) = 1.64 · 10 - 4 час -1.



