Лекция №13
Волновое уравнение
Схема “крест”
Гиперболическое волновое уравнение описывает колебания струны, движение сжимаемого газа, распространение электромагнитных волн и ряд других явлений.
Типичной одномерной задачей является задача описания малых колебаний натянутой струны с распределенной по длине нагрузкой f (t, x):
; (1)
; (2)
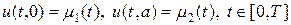. (3)
Уравнение колебания струны (1) дополняется начальными условиями (2), которые, в отличие от параболического уравнения требуют двух условий: начального смещения относительно положения равновесия u 0(x) и начальную скорость движения u 1(x). Кроме того, задаются краевые условия (3), которые называются краевыми условиями первого рода, они описывают смещение концов струны относительно положений равновесия. Краевые условия могут быть и иного рода.
Составим несложную, но эффективную разностную схему для численного решения задачи (1) — (3), выбирая для простоты равномерные по t и x сетки. В качестве шаблона разностной схемы возьмем, представленный на рис.1 шаблон в форме “креста”. Аппроксимируя производные в (1) конечными разностями, получим трехслойную схему следующего вида
, (4)
с граничными условиями
. (4¢)
Рис.1. Разностная схема (4) в форме креста
По форме шаблона схему (4) называют схемой “крест”. Исследуем схему крест.
Процедура вычисления решения выглядит следующим образом. На нулевом слое решение известно из начального условия
. (5)
На первом слое решение можно также вычислить по начальным данным. Простейший способ получения решения на первом слое состоит в аппроксимации второго начального условия в (2) согласно представлению:
. (6)
Аппроксимация (6) имеет первый порядок точности, тогда как в схеме крест разностный оператор второй производной по времени имеет второй порядок точности. Поэтому для более точной аппроксимации необходимо учесть еще один член разложения, т.е.
. (6¢)
Подставляя в (6¢) utt из (1), найдем
. (6¢¢)
Схема крест (4) является явной, поскольку позволяет выразить решение на следующем слое 
через значения yn и 
на двух предыдущих слоях. Поэтому, зная значения решения на нулевом (5) и первом слое (6¢¢), можно вычислить решения на всех последующих слоях. Итак, разностное решение существует и единственно.
Для изучения аппроксимации схемы крест, разложим точное решение по формуле Тейлора с центром в узле (tm, xn), считая все появляющиеся в разложении производные непрерывными:
Используя данные разложения, легко можно найти невязку схемы крест:
(7)
а также невязку начального условия (6):
,
или более точного начального условия (6¢¢):
(7¢)
Начальные (2) и краевые условия (3) аппроксимируются точно. В итоге разностная схема (4) с начальными условиями (5), (6¢¢) имеет порядок аппроксимации 
, а та же разностная схема с начальным условием (6¢) имеет несколько худший порядок — 
.
Устойчивость схемы крест исследуем методом разделения переменных, полагая
. (8)
Подставляя представление (8) в (4), для множителя роста гармоник находим квадратное уравнение
. (9)
По теореме Виета произведение корней квадратного уравнения (9) равно единице, т.е.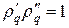 
. Условие устойчивости 
может таким образом быть выполнено при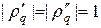 
. Это означает, что корни уравнения (9) должны образовывать комплексно сопряженную пару. Для этого необходимо, чтобы дискриминант уравнения (9) был неположительным для всех гармоник, т.е.
. (10)
Для выполнения неравенства (10) необходимо и достаточно соблюдение условия Куранта:
ct < h. (11)
В (11) стоит строгое неравенство, т.к., если верно равенство Куранта ct = h для некоторых гармоник, то появляется слабая неустойчивость из-за того, что корень квадратного уравнения (9) становится кратным.
В итоге разностная схема крест (4) с начальными условиями (5), (6¢) при выполнении условия Куранта (11) сходится с порядком аппроксимации . Из наших рассуждений следует, что сходимость имеет место в норме 
. Схема (4) обеспечивает хорошую точность расчета решения u (t, x), имеющих четвертую непрерывную производную. Схема позволяет также рассчитывать и менее гладкие решения.
Изучим аппроксимацию и сходимость схемы крест на численном примере решения уравнения (1) с правой частью, начальными и граничными условиями вида:
(12)
Нетрудно проверить, что решение задачи (1), (12) имеет следующее аналитическое решение:
. (13)
На листинге_№1 приведен код программы численного решения задачи (1), (12) с помощью разностной схемы крест (4) и начальными условиями (5), (6¢¢), т.е. с порядком аппроксимации .
Листинг_№1
%Программа решения волнового уравнения (1), (12) с
%помощью схемы крест (4)
function cross
global c
%Определяем габариты области интегрирования по времени T
%и пространству a, а также параметр c
T=1; a=2*pi; c=1;
%Определяем максимальное число удвоений числа узлов по
%времени и пространству smax
smax=6; N=2;
%Организуем основной цикл расчетов с различными сетками
for s=1:smax
%Определяем число узлов по пространству и удвоенное
%число узлов по времени
N=2*N; M=2*N;
%Определяем шаги по времени и пространству
tau=T/(M-1); h=a/(N-1);
r=(c^2*tau^2)/h^2;
%Определяем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
%Используем начальные данные из (12) для
%определения численного решения на первом и
%втором слое по формуле (6'')
for n=1:N
y(1,n)=-x(n)*sin(x(n));
y(2,n)=y(1,n)+tau*c*x(n)*cos(x(n))+...
0.5*tau^2*(c^2*(-2*cos(x(n))+...
x(n)*sin(x(n)))+f(0,x(n)));
end
%Определяем левое и правое граничные условия,
%взятые из (12)
for m=1:M
y(m,1)=0; y(m,N)=a*sin(c*t(m)-a);
end
%Применяем схему крест (4) к нашей задаче
for m=2:(M-1)
for n=2:(N-1)
y(m+1,n)=2*y(m,n)-y(m-1,n)+r*(y(m,n+1)-...
2*y(m,n)+y(m,n-1))+tau^2*f(t(m),x(n));
end
end
%Оцениваем зависимость предстепенной константы
%const=||y-u||/h^2 ошибки численного решения на
%последнем шаге по времени в норме C от h
for n=1:N
z1(n)=abs(y(M,n)-u(t(M),x(n)));
end
const(s)=max(z1)/h^2;
step(s)=h;
end
mi=0;
for m=1:5:M
mi=mi+1; ti(mi)=t(m); ni=0;
for n=1:5:N
ni=ni+1; xi(ni)=x(n); z(mi,ni)=y(m,n);
end
end
%Рисуем трехмерную поверхность решения в координатах
%время-пространство
subplot(1,2,1); surf(xi,ti,z);
%Рисуем график зависимости предстепенной константы от
%шага сетки
subplot(1,2,2); loglog(step,const);
%Определяем функцию правой части
function y=f(t,x)
global c
y=2*c^2*cos(c*t-x);
%Определяем аналитическое решение
function y=u(t,x)
global c
y=x*sin(c*t-x);
Рис.2. Численное решение волнового уравнения (1), (12) с помощью
схемы крест (4), (5), (6¢¢)
На рис.2 приведен итог работы кода программы листинга_№1. На левом рисунке приведен внешний вид численного решения 
, m = 1,…, M. На правом рисунке приведена зависимость предстепенной константы const в представлении зависимости ошибки численного решения 
от шага сетки, при этом шаг по времени выбирался порядка шага по пространству (при выполнении условия Куранта), т.е. t ~ h. Видно, что по мере уменьшения шага h величина const действительно выходит на некоторое постоянное значение, что подтверждает второй порядок аппроксимации схемы крест (4) с начальными условиями (5), (6¢¢).
Неявная схема
В схеме крест условие Куранта (11), обеспечивающее устойчивость, может быть достаточно обременительным. По этой причине построим неявную схему для задачи (1) — (3), которая будет безусловно устойчивой.
На рис.3 приведен шаблон искомой схемы. Составим по шаблону рис.3 следующую разностную схему с весами:
(14)
Рис.3. Шаблон разностной схемы (14)
Веса схемы (14) веса неотрицательны при 0 £ s £ ½. При s = 0 неявная схема (14) переходит в схему крест. Граничные и начальные условия можно определять по типу (4¢) и (5), (6¢¢) соответственно. На третьем и последующих слоях разностная схема представляет собой линейную систему уравнений с трехдиагональной матрицей, в которой имеет место диагональное преобладание, т.е. решение системы уравнений существует, единственно и вычисляется методом прогонки.
Аналогично схеме крест (4) можно показать, что неявная схема (14) на решениях с четвертыми непрерывными производными аппроксимирует задачу (1) — (3) с порядком при любых значениях параметра s.
Устойчивость схемы (14) изучим методом разделения переменных. Подставляя представление (8) в (14), получим уравнение для оценки множителя роста гармоники следующего вида:
(15)
Проводя рассуждения аналогичные тем, которые проводились при изучении уравнения (9), можно сделать вывод о том, что условие устойчивости выполняется, когда корни уравнения (15) комплексно сопряженные, что возможно только при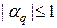 
. Из последнего неравенства следует условие устойчивости разностной схемы (14):
. (16)
Из неравенства (16) следует, что при s ³ ¼ схема (14) безусловно устойчива, когда s < ¼ схема (14) условно устойчива при 
.
В итоге, разностная схема (14) при выборе параметра веса ¼ £ s £ ½, безусловно сходится с точностью .
Решим численно задачу (1), (12), (13) с помощью неявной разностной схемы (14). На листинге_№2 приведен код соответствующей программы.
Листинг_№2
%Программа решения волнового уравнения (1), (12), (13)
%с помощью неявной схемы (14)
function implicit
global c
%Определяем габариты области интегрирования по времени T
%и пространству a, а также параметр c
T=10; a=2*pi; c=1;
%Определяем максимальное число удвоений числа узлов по
%времени и пространству smax
smax=6; N=4;
%Определяем весовую константу
sigma=0.25;
%Организуем основной цикл расчетов с различными сетками
for s=1:smax
%Определяем число узлов по пространству и равное
%число узлов по времени
N=2*N; M=N;
%Определяем шаги по времени и пространству
tau=T/(M-1); h=a/(N-1);
r=(sigma*c^2*tau^2)/h^2;
r2=((1-2*sigma)*c^2*tau^2)/h^2;
%Определяем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
%Используем начальные данные из (12) для
%определения численного решения на первом и
%втором слое по формуле (6'')
for n=1:N
y(1,n)=-x(n)*sin(x(n));
y(2,n)=y(1,n)+tau*c*x(n)*cos(x(n))+...
0.5*tau^2*(c^2*(-2*cos(x(n))+...
x(n)*sin(x(n)))+f(0,x(n)));
end
%Определяем левое и правое граничные условия,
%взятые из (12)
for m=1:M
y(m,1)=0; y(m,N)=a*sin(c*t(m)-a);
end
%Применяем неявную схему (14) к нашей задаче
for m=2:(M-1)
alpha(2)=0; beta(2)=y(m+1,1);
for n=2:(N-1)
alpha(n+1)=r/(1+r*(2-alpha(n)));
beta(n+1)=(r2*y(m,n-1)+(2-2*r2)*y(m,n)+...
r2*y(m,n+1)+r*y(m-1,n-1)-(1+2*r)*...
y(m-1,n)+r*y(m-1,n+1)+tau^2*...
f(t(m),x(n))+r*beta(n))/...
(1+r*(2-alpha(n)));
end
for n=N:-1:2
y(m+1,n-1)=alpha(n)*y(m+1,n)+beta(n);
end
end
%Оцениваем зависимость предстепенной константы
%const=||y-u||/h^2 ошибки численного решения на
%последнем шаге по времени в норме C от h
for n=1:N
z1(n)=abs(y(M,n)-u(t(M),x(n)));
end
const(s)=max(z1)/h^2;
step(s)=h;
end
mi=0;
for m=1:10:M
mi=mi+1; ti(mi)=t(m); ni=0;
for n=1:10:N
ni=ni+1; xi(ni)=x(n); z(mi,ni)=y(m,n);
end
end
%Рисуем трехмерную поверхность решения в координатах
%время-пространство
subplot(1,2,1); surf(xi,ti,z);
%Рисуем график зависимости предстепенной константы от
%шага сетки
subplot(1,2,2); loglog(step,const);
%Определяем функцию правой части
function y=f(t,x)
global c
y=2*c^2*cos(c*t-x);
%Определяем аналитическое решение
function y=u(t,x)
global c
y=x*sin(c*t-x);
На рис.4 приведен итог работы кода программы листинга_№2. На левом рисунке приведен внешний вид численного решения , m = 1,…, M. Обратим внимание на то, что использование неявной безусловно устойчивой схемы (14) позволило при том же приблизительно количестве узлов увеличить отрезок интегрирования по времени в десять раз по сравнению со схемой крест, которая является условно устойчивой. На правом рисунке приведена зависимость предстепенной константы const в представлении зависимости ошибки численного решения от шага сетки, при этом шаг по времени выбирался порядка шага по пространству, т.е. t ~ h. Видно, что по мере уменьшения шага h величина const действительно выходит на некоторое постоянное значение, что подтверждает второй порядок аппроксимации неявной схемы (14) с начальными условиями (5), (6¢¢), (12).
Рис.4. Решение волнового уравнения (1), (12), (13) с помощью неявной
разностной схемы (14)
Обобщим неявную разностную схему (14) на случай, когда скорость звука с является переменной. В этом случае уравнение (1) переписывается в виде:
, (17)
где k (t, x) º c 2(t, x) > 0. Будем считать, что функции k (t, x), f (t, x) в (17) кусочно-непрерывны, причем разрывы неподвижны, т.е. лежат на линиях x = const. Предполагается, что на разрывах выполняется условие сопряжения [ u ] = [ kux ] = 0, т.е. решение u и поток kux являются непрерывными функциями.
Выберем по времени равномерную сетку, а по пространству специальную неравномерную сетку, у которой все точки разрыва коэффициентов являются узлами. Построим аналог наилучшей консервативной схемы (11.19) — (11.21¢), разобранной в лекции №11:
, (18)
где
(18¢)
Известно[1], что при сделанных предположениях и при достаточно гладких начальных и граничных условиях схема (18), (18¢) равномерно сходится со скоростью 
при выполнении условия устойчивости (16).
Проведем численный расчет по разностной схеме (18), (18¢) задачи (17), (2), (3) в прямоугольной области G (t, x) = [0, T ]´[0, a ] при условии, что
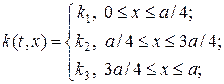(19)
(20)
где k 1, k 2, k 3, f 1, f 2, f 3 — некоторые постоянные величины. С учетом положений разрывов в (19), (20) определим равномерную сетку по пространству xn = nh, n = 1,…, N, где N = 4 l + 1, l = 1,2,… Определим также равномерную сетку по времени, т.е. tm = t m, 1,…, M. С учетом сделанных предположений рассмотрим следующую схему аппроксимации для интегралов в (18¢):
. (21)
В качестве начальных и граничных условий положим
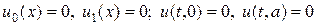. (22)
На листинге_№3 приведен код программы численного решения задачи (17), (19), (20), (22) с помощью наилучшей разностной схемы (18), (18¢), (21).
Листинг_№3
%Программа решения волнового уравнения (17), (19),
%(20) с помощью разностной схемы (18), (18'), (21)
function best_scheme
global a k1 k2 k3 f1 f2 f3
%Определяем габариты области интегрирования по
%времени T и пространству a
T=5; a=1;
%Определяем константы k1,k2,k3,f1,f2,f3
k1=1; k2=10; k3=1; f1=1; f2=10; f3=1;
%Определяем весовую константу
sigma=0.25;
%Определяем число узлов по пространству и времени
M=201; N=161;
%Определяем шаги по времени и пространству
tau=T/(M-1); h=a/(N-1);
r=(sigma*tau^2)/h^2;
r2=((1-2*sigma)*tau^2)/h^2;
%Определяем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
%Используем начальные данные из (22) для
%определения численного решения на первом и
%втором слое по формуле (6'')
for n=1:N
y(1,n)=0;
y(2,n)=y(1,n)+0.5*tau^2*f(x(n));
end
%Определяем левое и правое граничные условия,
%взятые из (22)
for m=1:M
y(m,1)=0; y(m,N)=0;
end
%Применяем неявную наилучшую схему (18), (18')
%к нашей задаче
for m=2:(M-1)
%Определяем коэффициенты прогонки
alpha(2)=0; beta(2)=y(m+1,1);
for n=1:(N-1)
kapa(n)=0.5*(k(x(n))+k(x(n+1)));
end
for n=2:(N-1)
alpha(n+1)=(r*kapa(n))/(1+r*(kapa(n)+...
kapa(n-1)*(1-alpha(n))));
beta(n+1)=(r2*kapa(n-1)*y(m,n-1)+...
(2-r2*(kapa(n-1)+kapa(n)))*y(m,n)+...
r2*kapa(n)*y(m,n+1)+r*kapa(n-1)*...
y(m-1,n-1)-(1+r*(kapa(n-1)+kapa(n)))*...
y(m-1,n)+r*kapa(n)*y(m-1,n+1)+0.25*...
tau^2*(f(x(n-1))+2*f(x(n))+f(x(n+1)))+...
r*kapa(n-1)*beta(n))/(1+r*(kapa(n)+...
kapa(n-1)*(1-alpha(n))));
end
for n=N:-1:2
y(m+1,n-1)=alpha(n)*y(m+1,n)+beta(n);
end
end
%Рисуем трехмерную поверхность решения в координатах
%время-пространство
surf(x,t,y);
%Определяем функцию квадрата скорости звука k(t,x)
function y=k(x)
global a k1 k2 k3
if (x>=0)&(x<=0.25*a)
y=k1;
end
if (x>0.25*a)&(x<0.75*a)
y=k2;
end
if (x>=0.75*a)&(x<=a)
y=k3;
end
%Определяем функцию правой части
function y=f(x)
global a f1 f2 f3
if (x>=0)&(x<=0.25*a)
y=f1;
end
if (x>0.25*a)&(x<0.75*a)
y=f2;
end
if (x>=0.75*a)&(x<=a)
y=f3;
end
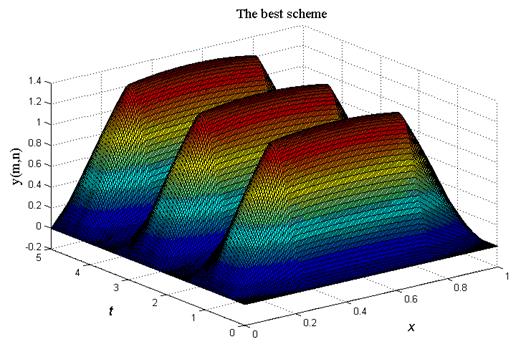
Рис.5. Численное решение волнового уравнения (17), (19), (20), (22) с
помощью наилучшей разностной схемы (18), (18¢), (21)
Итог работы кода программы листинга_№3 приведен на рис.5. На графике представлено решение в виде волны, что, конечно же, характерно для волнового уравнения (17). Плоскости разрывов x = a /4 и x = 3 a /4 просматриваются на поверхности решения.
Двухслойная акустическая схема
Волновое уравнение второго порядка может быть представлено в виде пары уравнений первого порядка. Рассмотрим систему уравнений
(23)
Покажем, что система (23), состоящая из пары уравнений первого порядка, сводится к волновому уравнению (1) второго порядка. Продифференцируем по x второе уравнение в (23) и подставим vx из первого уравнения, тогда получим
.
Полное совпадение с волновым уравнением (1) наступит при условии, что vx = ut и Fx = f. Если проинтегрировать последние два уравнения по x, то
. (24)
Величины (24) называются потенциалами скорости и правой части.
Начальные данные (2) с учетом (24) можно переписать в виде:
, (25)
где V — некоторая константа.
Граничные условия (3) остаются без изменения, т.е.
. (26)
В ряде случаев задача акустики (23) — (26) оказывается более удобной для численного решения, чем волновое уравнение (1). Построим и исследуем неявную разностную схему для решения уравнений акустики.
Рис.6. Шаблон разностной схемы (27), (27¢)
Возьмем в общем случае неравномерную сетку по пространству 0 = x 0 < x 1 < … < xN = a, в узлах которой определим величины 
, n = 0,1,…, N, а в серединах интервалов — величины 
, n = 0,1,…, N -1. Выберем шаблон разностной схемы, представленный на рис.6 и составим по нему разностную схему с весами:
, (27)
, (27¢)
где 
, 
и считается, что s 1, s 2 Î [0,1]. Шаблон схемы (27) выделен на рис.6 красным цветом (сплошные линии), шаблон схемы (27¢) — зеленым цветом (точечные линии).
Если положить 
, то схема (27) будет симметричной по переменной x и иметь порядок аппроксимации . Если положить s 1 = s 2 = ½ и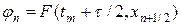 
, то порядок аппроксимации по времени схемы (27), (27¢) станет вторым, т.е. .
Как обычно устойчивость схемы (27), (27¢) изучим с помощью метода разделения переменных, представляя возмущения функций y и z в виде гармоник следующего вида:
. (28)
Гармоники для y и z в (28) взяты с одной и той же частотой и множителем роста, но с различными амплитудами. Подставляя (28) в (27), (27¢) и полагая 
, для амплитуд a и b получим однородную систему уравнений
(29)
Система линейных уравнений (29) имеет нетривиальное решение, когда ее определитель равен нулю. Это условие дает квадратное уравнение для определения множителя роста r:
, (30)
где
(31)
Каждый из двух корней уравнения (30) меньше по модулю единицы, если и только если
. (32)
Первое из неравенств в (32) следует из теоремы Виета 
, второе можно доказать с помощью несложных, но несколько громоздких выкладок. Неравенства (32) выполняются для всех гармоник, когда
, (33)
неравенства (33) являются условиями устойчивости для разностной схемы (27), (27¢).
Из неравенства (33) следует, что если s 1 ³ ½ и s 2 ³ ½, то схема (27), (27¢) является безусловно устойчивой. Если s 1 + s 2 ³ 1, но один из весов меньше ½, то схема условно устойчива 
. При s 1 + s 2 < 1 схема безусловно неустойчива.
Особо выделим симметричную схему, которая реализуется при s 1 = s 2 = ½. В этом случае разностная схема (27), (27¢) является безусловно устойчивой и сходится со скоростью . Данная схема является одной из лучших схем для задач акустики.
Разностная схема (27), (27¢) при произвольных значениях весов s 1 и s 2 решается путем определения 
из уравнения (27), т.е.
(34)
и подстановки и 
в (27¢), что приводит к уравнению
(34¢)
Согласно (34¢) для получения значений 
можно применить метод прогонки. Соответствующая трехдиагональная матрица обладает свойством диагонального преобладания, что обеспечивает существование и единственность решения задачи акустики с помощью разностных схем (27), (27¢) или, что тоже, уравнений (34), (34¢).
Численно изучим разностную схему (34), (34¢) на примере решения задачи акустики (24) при
, (35)
а также при начальных и граничных значениях вида:
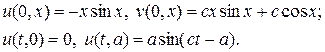(36)
Как нетрудно проверить уравнения акустики (23) при условии (35), (36) имеют следующее аналитическое решение:
. (37)
Аналитические решения (37) получены с помощь преобразования (24) при v (t,0) = c ×cos(ct), исходя из решений задачи (1), (12), (13).
На листинге_№4 приведен код программы численного решения задачи акустики (23), (35), (36) с помощью разностной схемы (34), (34¢).
Листинг_№4
%Программа численного решения задачи акустики
%(23) - (26) с помощью разностной схемы (34), (34')
function acoustics
global c
%Определяем габариты области интегрирования
%G=[0,T]x[0,a] и скорость звука c
T=8; a=2*pi; c=1;
%Выбираем для анализа симметричную схему, у которой
%весовые коэффициенты
sigma1=0.5; sigma2=0.5;
%Количество удвоений smax числа узлов сетки
smax=6; N=4;
%Организуем цикл расчетов по разностной схеме
%(34), (34') с различным числом узлов по
%пространству и времени
for s=1:smax
%Удваиваем число узлов по пространству
N=2*N;
%Считаем, что число узлов по времени равно
%числу узлов по пространству
M=N;
%Определяем шаги по времени и пространству
tau=T/(M-1); h=a/(N-1);
%Определяем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
r=(sigma1*sigma2*c^2*tau^2)/h^2;
r2=((1-sigma1)*sigma2*c^2*tau^2)/h^2;
%Определение начального распределения для u-y
%согласно (36)
for n=1:N
y(1,n)=u(t(1),x(n));
end
%Определение начального распределения для v-z
%согласно (36)
for n=1:(N-1)
z(1,n)=v(t(1),x(n)+0.5*h);
end
%Определение граничных условий для u-y
%согласно (36)
for m=1:M
y(m,1)=u(t(m),x(1));
y(m,N)=u(t(m),x(N));
end
%Организуем цикл расчетов по времени
for m=1:(M-1)
%Находим коэффициенты прогонки для вычисления u-y
alpha(2)=0; beta(2)=y(m+1,1);
for n=2:(N-1)
alpha(n+1)=r/(1+r*(2-alpha(n)));
beta(n+1)=(r2*y(m,n-1)+(1-2*r2)*y(m,n)+...
r2*y(m,n+1)+(tau/h)*(z(m,n)-z(m,n-1))+...
((sigma2*tau^2)/h)*(F(t(m)+0.5*tau,...
x(n)+0.5*h)-F(t(m)+0.5*tau,x(n-1)+...
0.5*h))+r*beta(n))/(1+r*(2-alpha(n)));
end
for n=N:-1:2
y(m+1,n-1)=alpha(n)*y(m+1,n)+beta(n);
end
%Вычисляем функцию v-z
for n=1:(N-1)
z(m+1,n)=z(m,n)+((c^2*tau)/h)*(sigma1*...
(y(m+1,n+1)-y(m+1,n))+(1-sigma1)*...
(y(m,n+1)-y(m,n)))+tau*F(t(m)+...
0.5*tau,x(n)+0.5*h);
end
end
%Находим ошибку численного решения в норме C
for m=1:M
for n=1:N
ery(m,n)=abs(y(m,n)-u(t(m),x(n)));
end
end
for m=1:M
for n=1:(N-1)
erz(m,n)=abs(z(m,n)-v(t(m),x(n)+0.5*h));
end
end
%Делим ошибку численного решения на h^2 и находим
%предстепенную константу в зависимости ошибки
%численного решения от шага сетки
const(s)=max(max(max(ery)),max(max(erz)))/h^2;
step(s)=h;
end
mi=0;
for m=1:10:M
mi=mi+1; ni=0;
for n=1:10:N
ni=ni+1; yi(mi,ni)=y(m,n);
end
end
%Рисуем численное решение функции u-y
subplot(1,3,1); surf(x([1:10:N]),t([1:10:M]),yi);
mi=0;
for m=1:10:M
mi=mi+1; ni=0;
for n=1:10:(N-1)
ni=ni+1; zi(mi,ni)=z(m,n);
end
end
%Рисуем численное решение функции v-z
subplot(1,3,2); surf(x([1:10:(N-1)]),t([1:10:M]),zi);
%Рисуем зависимость предстепенной константы
%const = max{||y-u||,||z-v||}/h^2 от шага сетки h
subplot(1,3,3); semilogx(step,const);
%Определяем функцию правой части
function y=F(t,x)
global c
y=-2*c^2*sin(c*t-x);
%Определяем аналитическое решение для u
function y=u(t,x)
global c
y=x*sin(c*t-x);
%Определяем аналитическое решение для v
function y=v(t,x)
global c
y=-c*x*sin(c*t-x)+c*cos(c*t-x);
На рис.7 приведен итог работы кода программы листинга_№4. На левом рисунке изображено численное решение u = u (tm, xn) » y (m, n), на среднем рисунке — v = v (tm, xn) » z (m, n). На правом рисунке изображена динамика предстепенной константы const в оценке ошибки численного решения симметричной схемы (s 1 = s 2 = ½) 
от шага по пространству h, при этом полагалось, что t ~ h. Видно, что при уменьшении шага сетки h предстепенная константа действительно выходит на некоторое постоянное значение.
Рис.7. Численное решение задачи акустики (24), (35), (36) с помощью
разностной схемы (34), (34¢)
Инварианты. Перепишем уравнения акустики с помощью инвариантов:
. (38)
Умножим первое уравнение в системе уравнений акустики (23) на c и в начале сложим оба уравнения друг с другом, а затем вычтем из второго уравнения первое, тогда получим
(39)
С учетом (25) нетрудно найти начальные данные для инвариантов:
. (40)
С учетом (26) определим краевые условия для инвариантов:
. (41)
Инвариант r удовлетворяет уравнению переноса вправо (c > 0), инвариант s — уравнению переноса влево. Для однородной задачи, когда F = 0, m 1 = m 2 =0, величины r, s переносятся по своим характеристикам без изменения, с чем и связано их наименование.
Для инвариантов можно составить разностные схемы, аналогичные разностным схемам для уравнения переноса. При этом шаблон каждой из схем должен учитывать направление характеристики данного уравнения. Рассмотрим простейшую явную разностную схему для уравнений (39):
. (42)
Схема (42) является схемой бегущего счета. Нетрудно показать, что при выполнении условия Куранта ct £ h схема устойчива и сходится с порядком точности 
на дважды непрерывно дифференцируемых функциях.
Изучим разностную схему для инвариантов на примере численного решения задачи (39) с помощью разностной схемы (42), выбирая правую часть, начальные и граничные условия согласно (35), (36). В этом случае при учете (40), (41), находим следующие выражения для правой части, начальных и граничных условий:
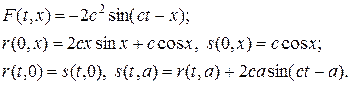(43)
Нетрудно проверить, что аналитическим решением задачи (39), (43) являются выражения вида:
. (44)
На листинге_№5 приведен код программы расчета задачи акустики в инвариантах (39) со специальной правой частью, начальными и граничными условиями (43).
Листинг_№5
%Программа решения уравнений акустики (39) в
%инвариантах с правой частью, начальными и
%граничными условиями вида (43)
function invariants
global c
%Определяем габариты области интегрирования по
%времени T и пространству a, а также определяем
%величину скорости c
T=2*pi; a=2*pi; c=1;
%Определяем число удвоений числа узлов сетки по
%времени и пространству dmax
dmax=5; N=4;
%Организуем цикл расчетов на различных сетках
for d=1:dmax
%Определяем число узлов сетки по пространству
%и времени
N=2*N; M=N;
%определяем шаги по времени и пространству
tau=T/(M-1); h=a/(N-1); kur=(c*tau)/h;
%Определяем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
%Определяем начальные условия (43) для
%инвариантов r и s
for n=1:N
r(1,n)=2*c*x(n)*sin(x(n))+c*cos(x(n));
s(1,n)=c*cos(x(n));
end
%Организуем цикл расчетов по времени
for m=1:(M-1)
%Осуществляем бегущий расчет инварианта r,
%осуществляемый слева направо
for n=2:N
r(m+1,n)=(1-kur)*r(m,n)+kur*r(m,n-1)+...
tau*F(t(m),x(n));
end
%Учитываем правое граничное условие (43)
s(m+1,N)=r(m+1,N)+2*c*a*sin(c*t(m+1)-a);
%Осуществляем бегущий расчет инварианта s,
%осуществляемый справа налево
for n=(N-1):-1:1
s(m+1,n)=(1-kur)*s(m,n)+kur*s(m,n+1)+...
tau*F(t(m),x(n));
end
%Учитываем левое граничное условие (43)
r(m+1,1)=s(m+1,1);
end
%Ошибку численного расчета инвариантов r и s
%оцениваем как разность численного и
%аналитического решений в норме C. Делим
%полученную ошибку на шаг по пространству h и
%находим предстепенную константу скорости
%сходимости схемы с инвариантами
for m=1:M
for n=1:N
er_r(m,n)=abs(r(m,n)-ra(t(m),x(n)));
er_s(m,n)=abs(s(m,n)-sa(t(m),x(n)));
end
end
const(d)=max(max(max(er_r)),max(max(er_s)))/h;
step(d)=h;
end
mi=0;
for m=1:5:M
mi=mi+1; ni=0;
for n=1:5:N
ni=ni+1;
ri(mi,ni)=r(m,n);
si(mi,ni)=s(m,n);
end
end
%Рисуем численное решение инварианта r
subplot(1,3,1); surf(x([1:5:N]),t([1:5:M]),ri);
%Рисуем численное решение инварианта s
subplot(1,3,2); surf(x([1:5:N]),t([1:5:M]),si);
%Рисуем график зависимости предстепенной
%константы от шага сетки h
subplot(1,3,3); semilogx(step,const);
%Определяем функцию правой части
function y=F(t,x)
global c
y=-2*c^2*sin(c*t-x);
%Определяем аналитический вид инварианта r
function y=ra(t,x)
global c
y=-2*c*x*sin(c*t-x)+c*cos(c*t-x);
%Определяем аналитический вид инварианта s
function y=sa(t,x)
global c
y=c*cos(c*t-x);
Рис.8. Решение задачи акустики (39), (43) в инвариантах
На рис.8 приведен итог работы кода программы листинга_№5. На левом рисунке приведено изображение численного решения инварианта r, на среднем рисунке — инварианта s. Правый график демонстрирует зависимость const от h в представлении для ошибки численного решения следующего вида:
,
где r (t, x), s (t, x) — аналитические решения (44). Из графика видно, что по мере уменьшения шага сетки h величина const действительно выходит на некоторое постоянное значение, при этом шаг по времени выбирался порядка шага по пространству, т.е. t ~ h. Это подтверждает также то, что скорость сходимости разностной схемы (42) — .
Многомерные схемы
Рассмотрим волновое уравнение в p -мерном пространстве следующего вида:
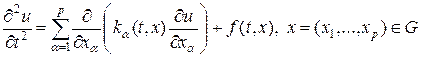. (45)
Решение задачи (45) предполагает определение начальных и краевых условий:
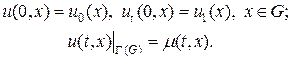(46)
Схема “крест” строится аналогично одномерной схеме (4) на шаблоне, вид которого для случая двух измерений показан на рис.9. При произвольном числе измерений разностная схема крест может быть записана в виде:
, (47)
при этом в случае переменных коэффициентов ka операторы L a определяются также как и для наилучшей схемы (18), (18¢).
Рис.9. Шаблон схемы крест в двумерном случае
Трехслойная схема (47) является явной. Вычисления с помощью схемы (47) одинаково просты для любого числа измерений. Легко проверить, что схема имеет порядок аппроксимации 
.
Исследуем устойчивость схемы (47) методом разделения переменных, считая коэффициенты ka постоянными. Для этого подставим в (47) многомерную гармонику, имеющую следующий вид на трех временных слоях:
.
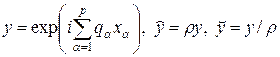В итоге для множителя роста r получим квадратное уравнение
. (48)
Анализ корней уравнения (48) показывает, что разностная схема (47) устойчива при условии, что
. (49)
Условие устойчивости (49) является аналогом условия Куранта (11).
Изучим схему крест на примере численного решения двумерной задачи (45), (46), когда k 1 = k 2 = c 2 = const > 0, т.е. решим ур