Метод разделения переменных

Метод разделения переменных широко используется для обоснования устойчивости многих линейных разностных схем. При помощи этого метода устанавливается устойчивость в норме .

Рассмотрим применение метода разделения переменных на примере явной разностной схемы решения уравнения теплопроводности (26), заданной на равномерной сетке 0 = x ₀ < x ₁ < … < x_N = a:

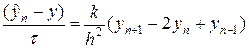. (71)

Погрешность решения 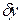уравнения (71) удовлетворяет такому же уравнению, т.е.

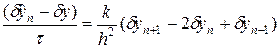. (71¢)

Решение уравнения (71¢) будем искать методом разделения переменных, т.е. в виде

. (72)

Подставляя (72) в (71¢), находим

. (73)

Можно сформулировать следующий признак устойчивости. Схема (71) с постоянными коэффициентами устойчива по начальным данным, если для всех q выполняется неравенство

, C = const. (74)

Доказательство. Система функций , q = 0,1,…, N - 1 полна и ортогональна на равномерной сетке x_n, n = 0,1,…, N. Разложим произвольную ошибку начальных данных в ряд Фурье по приведенной выше системе функций, тогда

.

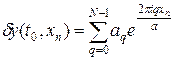В силу линейности уравнения (71¢) и представления (72), можно записать

.

Используя ортогональность гармоник, находим

(75)

Учитывая (74), (75), получаем выражение

,

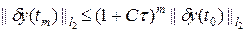которое совпадает с признаком устойчивости по начальным данным (60), т.е. утверждение доказано.

Применим признак устойчивости по начальным данным (74) к оценке (73). При C = 0 можно найти, что при любых q = 0,1,…, N - 1, когда , т.е. схема (71) является условно устойчивой.

Операторные неравенства

Общая теория устойчивости разностных схем, основанная на установлении неравенств между разностными операторами, построена А.А. Самарским[5]. Эта теория позволяет для многих линейных систем получить необходимые и достаточные условия устойчивости. Рассмотрим одно из таких условий устойчивости.

Напомним некоторые свойства операторов, отображающих гильбертово пространство на себя. Оператор A называется неотрицательным (A ³ 0), если (Ax, x) ³ 0 для любого ненулевого вектора x Î H, называется положительным (A > 0) при (Ax, x) > 0 и положительно определенным при (Ax, x) ³ e (x, x), e > 0. Неравенство A ³ B понимается в том смысле, что A - B ³ 0. При помощи положительного оператора A можно ввести так называемую энергетическую норму : .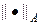

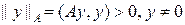Оператор A называется самосопряженным, если (Ax, y) = (x, Ay) для любых x, y Î H. Квадратным корнем из самосопряженного неотрицательного оператора A называется такой оператор B, что B × B = A. Оператор B обозначают A ^1/2, он существует, является самосопряженным и неотрицательным.

Исследуем устойчивость двуслойной разностной схемы, которая представлена в так называемой канонической форме:

. (76)

Теорема. Если операторы A и B самосопряженные, не зависят от номера слоя m и выполняется условие

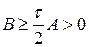, (77)

то схема (76) устойчива по начальным данным в энергетической норме 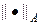, т.е.

. (78)

Доказательство. Для исследования устойчивости по начальным данным правую часть можно отбросить. Полагая j = 0 и умножая (76) слева на A ^1/2 B ^-1, найдем

. (79)

Введем новую переменную и преобразуем разностную схему (79) к виду

,

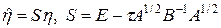при этом оператор S является самосопряженным.

Перепишем неравенство (77) в виде:

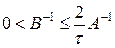. (80)

Умножим неравенство (80) слева и справа на положительный оператор A ^1/2, тогда

или в другой форме

.

Последнее неравенство позволяет записать следующую оценку

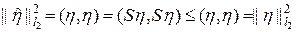. (81)

Норма же связана с энергетической нормой 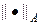простым соотношением:

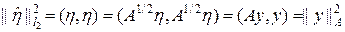. (82)

Из (81), (82) следует (78). Теорема доказана.

Сходимость

Рассмотрим дифференциальное уравнение с граничными условиями

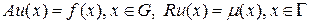. (83)

Для задачи (83) определим аппроксимирующую ее разностную схему на сетке, состоящей из регулярных и нерегулярных узлов w_h, g_h соответственно:

. (84)

Для изучения вопроса о сходимости нас будет интересовать близость разностного решения y (x) и точного решения u (x) на сетке w_h + g_h, при этом для сравнения естественно использовать одну из сеточных норм.

Определение. Разностное решение y (x) задачи (84) сходится к решению u (x) дифференциальной задачи (83), если

;

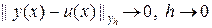разностное решение имеет порядок точности p, если

.

Определение. Разностная задача (84) корректна, если ее решение существует и единственно при любых входных данных j и c из соответствующих классов и схема устойчива.

Теорема [6]. Если решение u (x) задачи (83) существует, разностная схема (84) корректна и аппроксимирует задачу (83) на данном решении, то разностное решение сходится к точному.

Доказательство. Запишем цепочку преобразований:

,

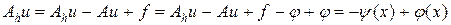где y (x) — невязка разностной схемы. Проводя аналогичные преобразования для граничных условий, получим

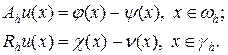(85)

Сравнивая (84) и (85), можно увидеть, что уравнения (85) являются разностными уравнениями (84) с модифицированной за счет невязки правой частью.

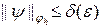Поскольку разностная схема устойчива, постольку для любого e > 0 найдется такое d (e), что , если и .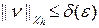

По определению аппроксимации для любого d > 0 найдется такое h ₀(d), что и при h £ h ₀(d).

Таким образом, для любого e > 0 найдется такое h ₀(d (e)), что при h £ h ₀(d (e)), т.е. имеет место сходимость. Теорема доказана.

[1] Плохотников К.Э. Математическое моделирование и вычислительный эксперимент. Методология и практика. — М.: Едиториал УРСС. 2003.

[2] Тихонов А.Н., Самарский А.А. Уравнения математической физики. — М.: Наука, Гл. ред. физ.-мат. литературы, 1972; Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. — М.: Высшая школа, 1970.

[3] Режимы с обострением. Эволюция идеи: Законы коэволюции сложных структур/ Сб. статей/ Ред. Г.Г. Малинецкий/ Кибернетика: неограниченные возможности и возможные ограничения. — М.: Наука, 1999. 255с.

© Из локальной близости функций следует их среднеквадратическая близость, поэтому ||·||_C называют более сильной, чем.

[4] Определение понятия устойчивости, обозначения и доказательства теорем с некоторыми модификациями заимствованы из учебного пособия: Калиткин Н.Н. Численные методы. — М.: Наука, Главная ред. физ.-мат. лит., 1978.

[5] Самарский А.А. Теория разностных схем. — М.: Наука, Главн. ред. физ.-мат. литературы, 1977.

[6] Данная теорема кратко еще формулируется таким образом: “Из аппроксимации и устойчивости следует сходимость”.