Правила и формулы вычисления производных

Краевой колледж предпринимательства

Учебное пособие для выполнения

практических и контрольных работ по "Математике"

раздел "Дифференциальное исчисление”

Пояснительная записка

Учебное пособие представляет собой руководство к решению задач раздела "Дифференциальное исчисление" курса "Элементы высшей математики" для студентов специальностей СПО на базе среднего (полного) общего образования.

Основное назначение пособия – помочь студенту самостоятельно, без помощи преподавателя изучить приемы решения основных задач, закрепить полученные навыки при выполнении практических работ и подготовиться к зачету (экзамену) по данному разделу.

ПРОИЗВОДНАЯ

Определение производной

Правила вычисления производных

Пусть дан график непрерывной функции y = f (x) (рис.)

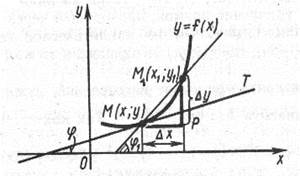Возьмем на кривой y = f (x) точки М (х; у) и М₁ (х₁; у₁), где х₁ = х + ∆х, у₁ = у + ∆у (∆х – приращение аргумента, ∆у – приращение функции). Проведем секущую ММ₁, угловой коэффициент которой обозначим через k_1, т.е. k₁ = tg φ₁. Из треугольника ММ₁Р находим .

Предположим, что точка М остается неподвижной, а точка М₁, перемещаясь по кривой, неограниченно приближается к М. Тогда:

1) Секущая ММ₁ поворачивается вокруг точки М, приближаясь к положению касательной;

2) х₁ → х, а следовательно, ∆х = (х₁ – х)→0;

3) угол φ₁ стремится к углу φ между касательной и осью Ох.

Пусть k – угловой коэффициент касательной, т.е. k =tgφ. Так как tg φ₁ – непрерывная функция (случай, когда φ₁ = , пока исключим из рассмотрения), то .

Итак, угловой коэффициент касательной определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю: .

Производной функции y = f (x) в данной точке х называют предел отношения приращения функции ∆у к соответствующему приращению аргумента ∆х при условии, что ∆х →0, т.е.

Вообще говоря, производная – это «новая» функция, произведенная от данной функции по указанному правилу.

ПРАВИЛА И ФОРМУЛЫВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ

Определение производной четко указывает действия, которые нужно выполнить для ее нахождения, что позволяет непосредственно вычислять производную любой элементарной функции. Непосредственное дифференцирование позволяет вывести основные правила и формулы дифференцирования.

Все правила и формулы дифференцирования сведем в таблицу и в дальнейшем будем пользоваться ею, подобно тому, как в арифметике пользуются таблицей умножения.

Пример 1.Найти производную функции у = х3 + 6х. Решение: у/ = (х3 +6х)/ = (х3)/ + (6х)/ = 3х2 + 6. Пример 2.Найти производную функции . Решение: Используя определение степени с отрицательным показателем, преобразуем данную функцию к виду 1 / х3 = х -3. Тогда получим у / = (х -3) / = -3 х -3 -1 = -3 х -4 = . Пример 3.Продифференцировать функцию у = 2х 3 (х6 – 1). Решение: 1 способ: используя правило IV, получим 2 способ: Предварительно преобразуем данную функцию: 2х 3 (х6 – 1)= 2х 9 – 2х 3. .   Пример 4.Продифференцировать функцию . Решение: .   Пример 5.Найти производную функции у = (х2+3х)5. Решение: Составляющими функции являются у = и5, и = х2 +3х. Согласно правилу VII, находим . Пример 6.Продифференцировать функцию y = sin2x. Решение: Порядок следования промежуточных функций таков: y = sin u, u = 2x.. Находим y/ = cos 2x (2x)/ = 2cos2x.