Приложения рядов Тейлора.

Ряд Тейлора. Разложение функции вещественной переменной в ряд Тейлора.

«Степенной ряд в области сходимости определяет бесконечно дифференцируемую функцию,
почленно дифференцируем и интегрируем »

Можно ли функцию, имеющую производные любого порядка, представить степенным рядом?

Из ДИФОП известно:

Очевидно, что формула Тейлора порядка «n» представляет равенство S(x)=S_n(x)+R_n(x) для сходящегося в O(x₀,r) степенного ряда , причем полином Тейлора порядка “n” является “n”- ой частичной суммой ряда S_n(x)=T_n(x,x₀), а остаток формулы Тейлора – суммой остатка ряда. Поэтому, если предел остатка формулы Тейлора , степенной ряд в точке «х» «сходится к значению функции» S(x)=f(x).

Утверждение.

«Если производные бесконечно-дифференцируемой функции “f” ограничены по модулю в некоторой r -окрестности точки х₀ (), степенной ряд сходится абсолютно в этой окрестности и его сумма S(x) определяет
«степенной ряд Тейлора для функции f в окрестности точки х₀»:

S(x)=f(x)

Алгоритм разложения функции в ряд Тейлора.

1) Вычисляются значения функции и ее производных в точке дифференцируемости, и записывается степенной ряд

2) Находится радиус сходимости r_CX =r этого степенного ряда.

3) Записывается разложение функции в СТР: .

Пример. Разложить вСТР Тейлорафункцию f(x)=ln(1+x) в окрестности точки х₀ =0.

2)

==================================================================

Замечания.

1) Для разложения в ряд Тейлора дробно-рациональных функций можно использовать степенной ряд бесконечно-убывающей геометрической прогрессии .

Например,

2) Разложение функции в ряд Тейлора можно получить, используя свойство почленного дифференцирования и интегрирования степенного ряда.

Например,

!!! Обратите внимание: полученный степенной ряд представляет разложение функции f(x)=arctg(x) в ряд Тейлора в окрестности точки х₀=0 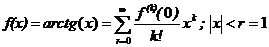и, следовательно, его коэффициент при x^k равен :

Ряды Тейлора для функций e^x, sin(x), cos(x), ln(1+x).

Ряды Тейлора для элементарных функций

можно найти в справочнике Г.Б. Двайта.

Приложения рядов Тейлора.

«Еще одно, последнее сказанье……»

I]. Вычисление приближенных значений аналитической функции в точке.

Пусть задано/получено разложение функции в степенной ряд в O(x₀,r)

, |x-x₀|<r (1)

За приближённое значение функции в точке f(a) примем оценку суммы числового ряда (1) в точке.

Пример. Вычислить значение функции sin(1рад) с погрешностью ε ≤ 0.001

è Запишем ряд Тейлора для функции sin(t)

и найдем оценку суммы числового ряда в точке t=1 с погрешностью ε ≤ 0.001:

sin(1)∊[S₄;S₃] = [0.8414; 0.8417],δ=0.0003<0.001

sin(1)=0.841471…? [0.8414; 0.8417]

2]. Интегрирование функций.

Из курса ИИФОП известно,

что вычисление определенного интеграла от функции f(x ) по формуле Ньютона-Лейбница
сводится к приближённому вычислению разности значений первообразной функции.

Рассмотрим еще один способ приближенного интегрирования функции – с помощью разложения подынтегральной функции в степенной ряд, почленного интегрирования этого ряда и получения оценки интеграла как оценки суммы полученного числового ряда.

Пример. Вычислить приближенное значение Si(1) интегрального синуса с погрешностью 0.0001.
SOS! Первообразная функции не выражается через конечную комбинацию элементарных функций.

è(1) Запишем степенной ряд для подынтегральной функции:

(3) Запишем соответствующий числовой ряд Si(1) и найдём оценку его суммы с заданной погрешностью:

ТР2.6 Часть-2. «Степенные ряды».

Задание: «Вычислить значение интеграла с точностью ε ≤ 0.0001.

2.1Разложитьподынтегральную функцию в степенной ряд. 2 балла
Указатьрадиус сходимости ряда.

2.2 Проинтегрировать степенной ряд почленно и получить числовой ряд. 2 балла
2.3 Получить оценку суммы числового ряда с заданной погрешностью. 2 балла
Максимум – 6 баллов; Зачет ≥ 4 балла

Пример выполнения.