Методы решения систем линейных уравнений
Задачи аппроксимации функции, а также множество других задач прикладной математики м вычислительной физики сводятся к задачам о решении систем линейных уравнений. Самым универсальным методом решения системы линейных уравнений является метод последовательного исключения неизвестных, называемый методом Гаусса.
Для иллюстрации смысла метода Гаусса рассмотрим систему линейных уравнений:
 (1)
(1)
Эту систему запишем в матричном виде:
 (2)
(2)
Как известно, обе части уравнения можно умножить на ненулевое число, а также можно из одного уравнения вычесть другое. Используя эти свойства, постараемся привести матрицу системы (2) к треугольному виду, т.е. к виду, когда ниже главной диагонали все элементы – нули. Этот этап решения называется прямым ходом.
На первом шаге прямого хода умножим первое уравнение на  и вычтем из второго, тогда исключится переменная
и вычтем из второго, тогда исключится переменная  из второго уравнения. Затем, умножим первое уравнение на
из второго уравнения. Затем, умножим первое уравнение на  и вычтем из третьего, тогда система (2) преобразуется в систему вида:
и вычтем из третьего, тогда система (2) преобразуется в систему вида:
 (3)
(3)
На втором шаге прямого хода из третьего уравнения исключаем  , т.е. из третьего уравнения вычитаем второе, умноженное, на
, т.е. из третьего уравнения вычитаем второе, умноженное, на  , что приводит систему (3) к треугольному виду (4)
, что приводит систему (3) к треугольному виду (4)
 (4)
(4)
Систему (4) переписываем в привычном виде:
 (5)
(5)
Теперь, из системы (5) можем находить решение в обратном порядке, т.е. сначала находим из третьего уравнения  , далее, подставляя во второе уравнение, находим
, далее, подставляя во второе уравнение, находим  . Подставляя
. Подставляя  и
и 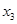 в первое уравнение системы (5), находим
в первое уравнение системы (5), находим  . Нахождение решения
. Нахождение решения  из системы (5) называют обратным ходом.
из системы (5) называют обратным ходом.
Теперь, на основе рассмотренного примера, составим общий алгоритм метода Гаусса для системы:
 (6)
(6)
Метод Гаусса состоит из двух этапов:
а) прямой ход – когда матрица системы (6) приводится к треугольному виду;
б) обратный ход – когда последовательно вычисляются неизвестные в обратном порядке, т.е. в последовательности:  .
.
а) Прямой ход: для приведения системы (6) к треугольному виду, уравнения с ненулевыми коэффициентами при переменной  переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами
переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами 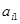 . Далее, вычитаем первое уравнение, помноженное на
. Далее, вычитаем первое уравнение, помноженное на  , из второго уравнения, вычитаем первое уравнение, помноженное на
, из второго уравнения, вычитаем первое уравнение, помноженное на  , из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на
, из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на 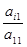 , из
, из  - го уравнения при
- го уравнения при  , если
, если  . Вследствие этой процедуры, мы обнулили все коэффициенты при переменной
. Вследствие этой процедуры, мы обнулили все коэффициенты при переменной  в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид:
в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид:
 (7)
(7)
Далее, применяем туже самую процедуру, для уравнений системы (7), начиная со второго уравнения, т.е. первое уравнение исключается из «игры». Теперь стараемся обнулить коэффициенты при переменной  , начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если
, начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если 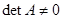 , то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде:
, то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде:
 (8)
(8)
б) Обратный ход: Вычисляем неизвестные по формулам:
 (9)
(9)
Замечание: для вычисления определителя системы можно использовать треугольную форму полученной матрицы, тогда определитель этой матрицы равен произведению диагональных элементов, т.е.
 (10)
(10)