Отчёт по лабораторной работе.
Цель работы: экспериментальное определение положения центра изгиба тонкостенного стержня открытого профиля; сравнение результатов расчета и эксперимента.
Постановка работы. На лабораторной установке проведено экспериментальное определение положения центра изгиба тонкостенного стержня с незамкнутым кольцевым сечением с записью в табл. координаты Х, точки приложения силы P, показания левого Uлi и правого Uпi индикаторов. Результаты экспериментов рекомендуется статистически обрабатывать по методу наименьших квадратов с определением параметров mл и Uл0, mп и Uп0, прямых Un и Uл.
Требуется: определить положение центра изгиба аХэ: графически как абсциссу точки пересечения прямых Uл – Х и Un – X; по формуле
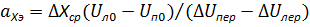; по результатам статобработки
; оценить расхождение расчетного ах = 2R = 57,4 мм и экспериментальных аХэ, значений 
; объяснить причины расхождений.
Таблица 1. Результаты эксперимента
| № | Xi, мм | ∆Xi, мм | Uлi, дел | ∆Uлi, дел | Uпi, дел | ∆Uпi, дел |
| _ | _ | _ | ||||
| -11 | ||||||
| -3 | ||||||
| -11 | ||||||
| -12 | ||||||
| -3 | ||||||
| -11 |
1. Проводим обработку приведенных в табл. результатов эксперимента и получаем:
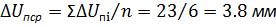
Uл0=66; Uп0=1 дел.
2. Определяем приближенное экспериментальное значение абсциссы центра изгиба тонкостенного стержня открытого профиля по формуле
3. Находим приближенное положение центра изгиба наглядным графическим методом как точку пересечения экспериментальных прямых 
и 
, построенных по результатам эксперимента 
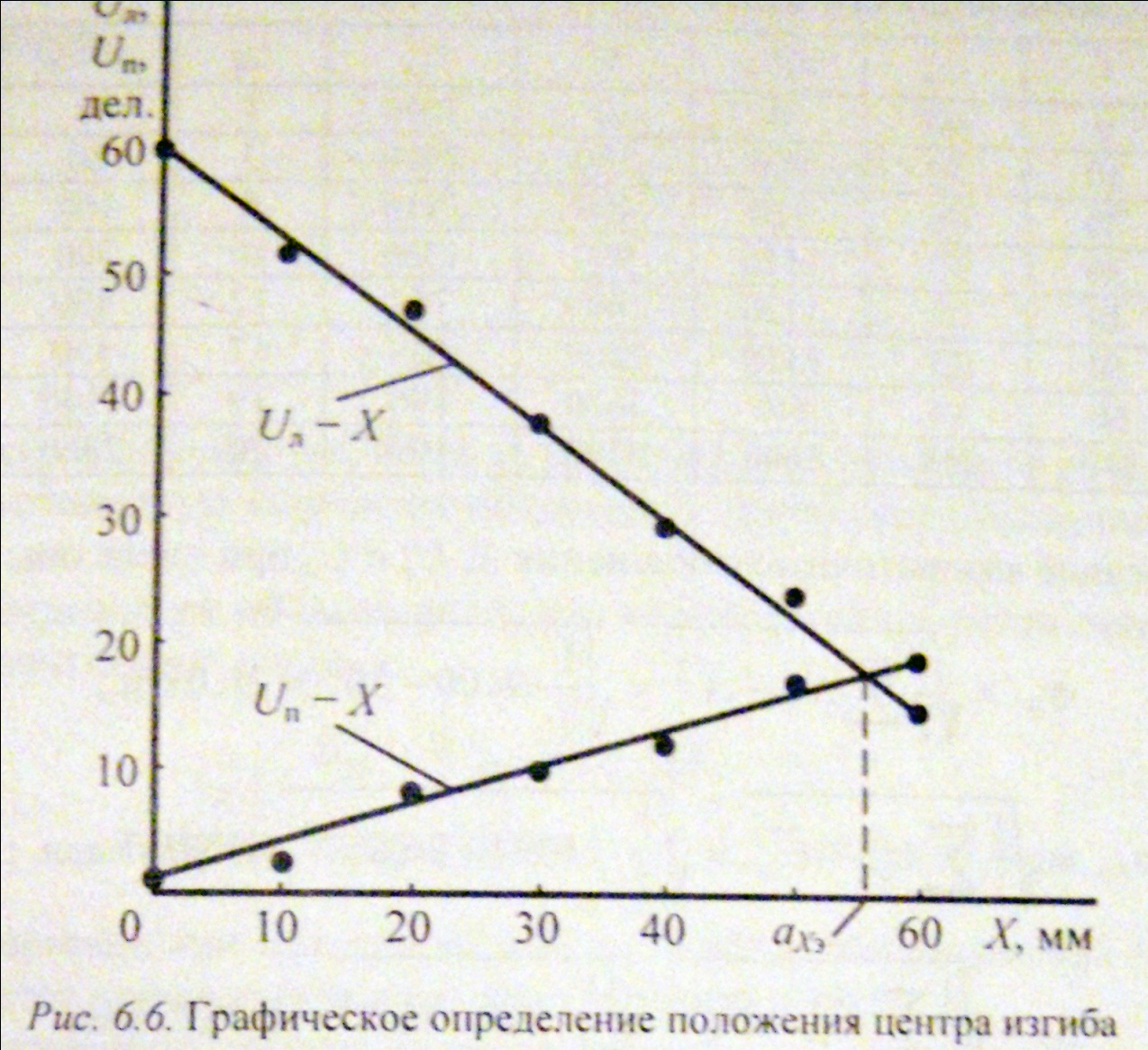
4. Из рис. видно, что экспериментальные точки не всегда располагаются на прямых и , т.к. наблюдается некоторое рассеивание опытных данных. При графическом определении 
, прямые проводились приближенно. В связи с этим для однозначного определения центра изгиба проведем статистическую обработку результатов эксперимента, используя метод наименьших квадратов. Уравнения прямых для левого и правого индикаторов представим следующим образом: 
и 
, где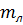 
, 
, 
, 
– искомые параметры прямых. По результатам экспериментов заполняем табл.
4.1 Средние значения координаты точки приложения силы Р, показаний левого и правого индикаторов:
;
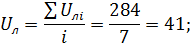
Таблица Данные для стат. обработки опытных результатов
| N п/п | 
| 
| 
| 
| 
| 
| 
| 
|
| ∑ |
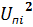
4.2 Средние квадратичные отклонения Х, Uл и Un при числе опытов
;
;
Смешанные центральные моменты первого порядка:
4.3 Тангенсы углов наклона прямых для левого и правого индикаторов:
4.4 Отрезки, отсекаемые прямыми 
, на оси ординат:
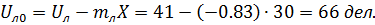
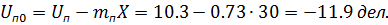
4.5 Коэффициенты корреляции опытных данных для левого и правого индикаторов:
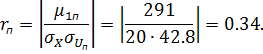
Близкие к единице значения коэффициентов корреляции 
и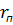 
подчеркивают устойчивую корреляционную связь полученных экспериментальных данных.
4.6 Определяем положение центра изгиба по результатам стат. обработки экспериментальных данных:
При применении для стат. обработки ПЭВМ рассмотренный пример рекомендуется использовать в качестве тестовой задачи.
4.7 Отклонение расчета от эксперимента
Выводы:
1. Экспериментальные значения 
, полученные тремя способами, практически совпадают между собой. Это обусловлено тем, что в данном варианте наблюдается малое рассеивание результатов эксперимента.
2. Отклонение результатов расчета от экспериментов обусловлено рядом принимаемых допущений при выводе формул, а также систематическими и случайными ошибками при проведении экспериментов. В целом методика расчета положения центра изгиба пригодна для практического использования.