УЧЕТ КОМПЛЕКСНОГО ХАРАКТЕРА
ПАРАМЕТРОВ СХЕМЫЗАМЕЩЕНИЯ И РЕЖИМА [1]
Система уравнений узловых напряжений для цепи переменного тока:
 . .
| (9.7) |
При решении на ЭВМ системы уравнений узловых напряжений для сети переменного тока, как правило, она приводится к системе действительных уравнений порядка 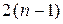 , где
, где  - число узлов схемы. Для этого представляют матрицы и вектор - столбцы с комплексными элементами в виде сумм матриц и вектор - столбцов с действительными элементами (при этом надо в виде такой суммы представить каждый комплексный элемент и учесть правило сложения матриц):
- число узлов схемы. Для этого представляют матрицы и вектор - столбцы с комплексными элементами в виде сумм матриц и вектор - столбцов с действительными элементами (при этом надо в виде такой суммы представить каждый комплексный элемент и учесть правило сложения матриц):
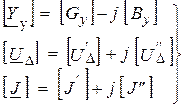
| (9.8) |
Подставляя (9.8) в (9.7), получим:

| (9.9) |
Уравнение (9.9) переписываем, разделяя действительные и мнимые слагаемые.
 . .
| (9.10) |
 . .
| (9.11) |
Иными словами, систему уравнений узловых напряжений для цепи переменного тока можно записать в виде блочного матричного уравнения:

| (9.12) |
Выражение (9.12) является системой действительных уравнений порядка 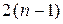 и содержит
и содержит 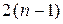 неизвестных действительных и мнимых составляющих узловых напряжений, представленных в форме действительных чисел.
неизвестных действительных и мнимых составляющих узловых напряжений, представленных в форме действительных чисел.
ОПИСАНИЕ РАСЧЕТА УР С ПОМОЩЬЮ ВЕКТОР-ФУНКЦИИ
Нелинейные уравнения установившегося режима в общей форме можно записать в виде системы неявных функций:
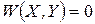
| (9.53) |
где  - вектор-функция.
- вектор-функция.
Эти уравнения связывают между собой параметры установившегося режима электрической системы. Часть параметров режима задана (независимые переменные 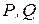 ). Обозначим вектор-столбец независимых переменных при расчете установившегося режима
). Обозначим вектор-столбец независимых переменных при расчете установившегося режима  . Остальные (зависимые переменные
. Остальные (зависимые переменные 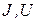 ) могут быть найдены из уравнений установившегося режима. Обозначим вектор-столбец зависимых переменных
) могут быть найдены из уравнений установившегося режима. Обозначим вектор-столбец зависимых переменных  .
.
Число зависимых переменных 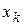 равно числу уравнений установившегося режима. Это означает, что вектор-функция
равно числу уравнений установившегося режима. Это означает, что вектор-функция  и вектор-столбец
и вектор-столбец  имеют одинаковую размерность. В зависимости от постановки задачи и способов задания исходных данных в состав векторов независимых и зависимых переменных
имеют одинаковую размерность. В зависимости от постановки задачи и способов задания исходных данных в состав векторов независимых и зависимых переменных  и
и  могут входить разные параметры режима.
могут входить разные параметры режима.
Разделение параметров режима на зависимые и независимые переменные играет важную роль при оптимизации режимов, при определении предельных по статической апериодической устойчивости режимов и при исследовании существования и единственности решения уравнений установившегося режима.
При расчетах установившегося режима вектор независимых переменных задан, то есть  , следовательно, нелинейную систему уравнений (9.53) можно переписать как
, следовательно, нелинейную систему уравнений (9.53) можно переписать как

| (9.54) |
Число уравнений в этой системе также равно числу зависимых переменных 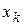 , то есть равно размерности вектора
, то есть равно размерности вектора  . В результате решения уравнений УР можно найти все зависимые переменные
. В результате решения уравнений УР можно найти все зависимые переменные 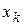 .
.
МЕТОД НЬЮТОНА
Метод Ньютона для решения систем нелинейных уравнений представляет собой обобщение на многомерный случай метода касательных, применяемого для решения одного нелинейного уравнения.
Идея метода Ньютона состоит в последовательной замене на каждой итерации системы нелинейных уравнений некоторой линейной системой, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение. Поясним идею этого метода на примере решения уравнения
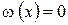
| (5.4) | |
Решение уравнения 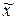 - точка, в которой кривая - точка, в которой кривая  проходит через нуль (рисунок 5.1):
Рисунок 5.1- Графическая иллюстрация метода Ньютона проходит через нуль (рисунок 5.1):
Рисунок 5.1- Графическая иллюстрация метода Ньютона
| 
| |
Зададим начальное приближение к решению уравнения 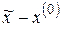 и вычислим значение функции
и вычислим значение функции 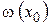 . Если точка
. Если точка  достаточно близка к решению, то для его получения целесообразно разложить функцию
достаточно близка к решению, то для его получения целесообразно разложить функцию 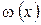 в ряд Тейлора в окрестностях точки
в ряд Тейлора в окрестностях точки  :
:

| (5.5) |
Выражению (5.5) соответствует касательная к функции, проведенная в точке  . Такая касательная показана на рисунке 5.1. Для малых значений
. Такая касательная показана на рисунке 5.1. Для малых значений 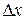 приближение (5.5) хорошо моделирует саму функцию
приближение (5.5) хорошо моделирует саму функцию 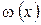 , поэтому в качестве приближенного решения исходного уравнения целесообразно использовать решение
, поэтому в качестве приближенного решения исходного уравнения целесообразно использовать решение  линеаризованного уравнения (5.5), равное
линеаризованного уравнения (5.5), равное
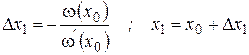
| (5.6) |
Полученную точку  можно использовать в качестве нового приближения и сделать шаг, в результате которого будет найдено приближение
можно использовать в качестве нового приближения и сделать шаг, в результате которого будет найдено приближение 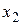 и т. д. Итерационный процесс получения решения показан на рисунке 5.1.
и т. д. Итерационный процесс получения решения показан на рисунке 5.1.
Аналогично определяется решение для системы нелинейных уравнений. Рекуррентное выражение, представленное в матричной форме записи, имеет вид:

| (5.7) |
где  - матрица Якоби (или якобиан), составленная из частных производных;
- матрица Якоби (или якобиан), составленная из частных производных;
 - вектор невязок, вычисленный в точке
- вектор невязок, вычисленный в точке 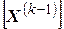 ;
;
 - вектор поправок к
- вектор поправок к 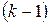 приближению
приближению 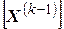 .
.
Пример использования метода Ньютона для решения УУН
Для электрической сети, представленной на рисунке 5.2, определить напряжения в узлах, используя метод Ньютона (три итерации).
Для рассматриваемой схемы электрической сети может быть записана система нелинейных УУН в форме баланса токов:
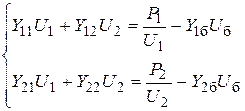
| (5.8) |

| |
| Рисунок 5.2 | Схема электрической сети. |
Для решения методом Ньютона система УУН (5.8) представляется в форме баланса мощностей
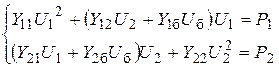
| (5.9) |
И приводится к виду

|
Рекуррентное выражение метода Ньютона:
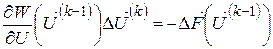 , ,
| (5.10) |
Где: 1) элементы матрицы Якоби вычисляются по формулам:
 , ,
|
2) вектор невязок вычисляется в точке  по следующим выражениям:
по следующим выражениям:
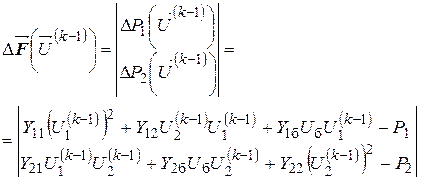 , ,
|
3)  - вектор поправок к
- вектор поправок к 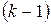 -му приближению
-му приближению  .
.
Новые напряжения вычисляются по выражению

| (5.11) |
Для схемы электрической сети, представленной на рисунке 5.2, исходная система (5.9) имеет вид:

|
Итерация 1
Начальное приближение: 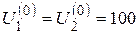 кВ
кВ
Вектор невязок записывается: 
Элементы матрицы Якоби:
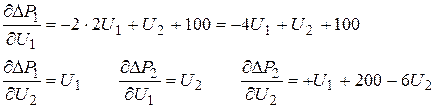
|
Для заданного начального приближения 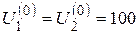 кВ элементы матрицы Якоби приобретают значение
кВ элементы матрицы Якоби приобретают значение

|
Подставляем все найденные величины в  и получаем систему двух линейных уравнений:
и получаем систему двух линейных уравнений:

|
Решив ее, находим:

|
По выражению (5.11):
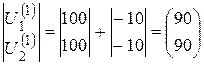 кВ кВ
|
Итерация 2
Вектор невязок:

|
Матрица Якоби:

|
Система двух линейных уравнений:

|
Решив ее, находим:

|
По выражению (5.11):
 кВ кВ
|
Итерация 3
Вектор невязок:
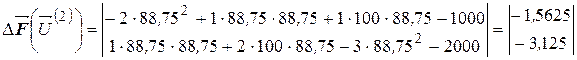
|
Матрица Якоби:

|
Система двух линейных уравнений:

|
Решив ее, находим:

|
По выражению (5.11):
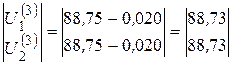 кВ кВ
|
Вектор невязок для 4-ой итерации составил бы:

|
| Алгоритмизация задач энергетики Екатеринбург, 1999. |