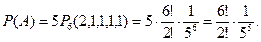Полиномиальные испытания

Глава 4. Повторные независимые испытания. Теорема Бернулли.

Испытания Бернулли.

Теория вероятностей имеет дело с такими экспериментами, которые можно повторять, по крайней мере теоретически, неограниченное число раз. Пусть некоторый эксперимент повторяется n раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений часто называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:

1) результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей»;

2) вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний.

Теорема Бернулли. Если производится серия из n независимых испытаний Бернулли, в каждом из которых успех появляется с вероятностью р, то вероятность того, что успех в n испытаниях появится ровно m раз, выражается формулой

P_n(m)=C_n^mp^mq^n-m, где q=1-p – где вероятность неудачи.

 

Эта формула называется формулой Бернулли.

Задача 1. Игральная кость бросается 6 раз. Найти вероятность того, что ровно 3 раза выпадет «шестерка».

Решение. Пятикратное бросание кости можно рассматривать как последовательность независимых испытаний с вероятностью успеха («шестерки») равно 1/6 и вероятностью неудачи — 5/6. Искомую вероятность найдем по формуле .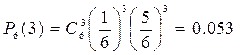

Задача 2. Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.

Решение. Искомая вероятность равна сумме трех вероятностей

Р = Р₆(0) + Р₆(1) + Р₆(2) = .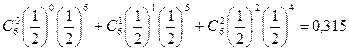

 

Наивероятнейшее число успехов.

 

Число m, при котором биномиальные вероятности P_n(m) достигают своего максимального значения (при фиксированном числе испытаний n) называют обычно наиболее вероятным (наивероятнейшим) числом успехов. Справедливо следующее утверждение о наивероятнейшим числе успехов:

Наивероятнейшее число успехов m* в серии из n независимых испытаний Бернулли (с вероятностью успеха р в одном испытании) определяется соотношением np-q£m*£np+p, причем

1. если число np-q - дробное, то существует одно наивероятнейшее число m*;

Если число np-q - целое, то существует два наивероятнейших числа

m*=np-q, m*=np+p;

3. если np - целое число, то наивероятнейшее число m*=np.

Задача 3. Монета подбрасывается 3 раза. Найти наиболее вероятное число успехов (выпадений герба).

Решение. Возможными значениями для числа успехов в 3-х рассматриваемых испытаниях являются m = 0, 1, 2 или 3. Пусть A_m - событие, состоящее в том, что при 3-х подбрасываниях монеты герб появляется m раз. По формуле Бернулли легко найти вероятности событий A_m (см. таблицу):

m
Pn(m)	1/8	3/8	3/8	1/8

Из этой таблицы видно, что наиболее вероятными значениями являются числа 1 и 2 (их вероятности равны 3/8). Этот же результат можно получить и из приведенного выше утверждения.

 

Задача 4. Вероятность получения удачного результата при производстве сложного химического опыта равна ¾. Найти наивероятнейшее число удачных опытов, если общее их количество равно 10.

Решение. В этом примере n=10, p=3/4=0,75, q=1/4=0,25. Тогда неравенство для наиболее вероятного числа успехов выглядит так:

np-q£m*£np+p,

т.е. 10*0,75-0,25 £m*£10*0,75+0,75,

или 7,25£m*£8,25.

Существует только одно целое решение этого неравенства, а именно, m*=8.

 

Приближенные формулы.

 

При больших n непосредственное вычисление вероятностей P_n(m) по формуле Бернулли сопряжено с трудностями вычислительного порядка, поэтому в таких случаях используют различные варианты приближенных вычислений, основанные на предельных теоремах Пуассона и Муавра‑Лапласа.

А. Приближенная формула Пуассона используется в том случае, когда число испытаний Бернулли (n) – велико, а вероятность успеха в отдельном испытании мала (p<0,1). Тогда

P_n(m)»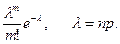

Задача 5. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей?

Решение. Имеем 1000 испытаний Бернулли с вероятностью «успеха» р=0,005, и npq <5. Применяя пуассоновское приближение с np=5, получаем

P₁₀₀₀(3)» 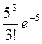, P₁₀₀₀(m³3)=1-P₁₀₀₀(m<3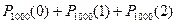)= 1-[ ] »1- 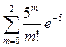и по таблицам находим Р₁₀₀₀(3)»0,14, Р₁₀₀₀(m³3)»0,875.

 

В силу определенной «симметричности» понятий «успех» и «неудача» приближенная формула Пуассона может использоваться в схеме независимых испытаний Бернулли также и в случае, когда р близко к единице (т.е. q<0,1), а nq - не велико и не мало:

P_n(n-m)=C_n^n-mp^n-mq^m=C_n^mp^n-mq^m »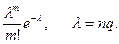

 

Б. Приближенные формулы Муавра – Лапласа. Если в схеме независимых испытаний Бернулли число испытаний n велико, а вероятности успеха и неудачи не малы (например, 0,1<p<0,9), то вероятность P_n(m) появления ровно m успехов в n испытаниях вычисляется по формуле (локальная теорема Муавра-Лапласа):

P_n(m)=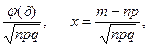

где j(х)= 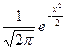. Функция j(х) – четная и для положительных значений х составлена таблица ее значений.

Задача 6. Вероятность поражения мишени стрелком при одном выстреле р=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

Решение. Здесь n=10, m=8, p=0,75, q=0,25. Найдем х= 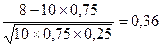, и по таблице определяем j (x)=0,3739, тогда искомая вероятность равна

Р₁₀(8)= .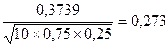

 

Для вычисления вероятности P_n(m₁,m₂)= P(m₁£m£m₂) события, состоящего в том, что число успехов в n испытаниях Бернулли окажется заключенным в пределах от m₁ до m₂, используется следующая приближенная формула (интегральная теорема Муавра-Лапласа):

P_n(m₁,m₂)»Ф(x₂)‑Ф(x₁),

где x₁= 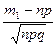, x₂= 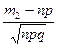, а Ф(х)= 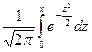- функция Лапласа.

Функция Ф(x) равна 0 при x=0; Ф(-х)º-Ф(x) для всех x, то есть симметрична относительно x=0. Для функции Ф(х) составлены специальные таблицы при положительных значениях аргумента.

 

Задача 7. Вероятность появления события А в каждом из 21 независимых испытания равна 0,7. Найти вероятность того, что событие А появится в большинстве испытаний.

Решение. х₁= 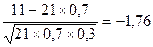. Аналогично подсчитывается х₂ = 3. Тогда Р(11£m£21)=Ф(х₂)–Ф(х₁)=0,49865+0,4608=0,9594.

 

Используя интегральную формулу Муавра-Лапласа можно вычислить вероятность того, что частота появления успеха в n независимых испытаниях Бернулли (т.е. число m/n) отклонится от вероятности успеха не более чем на положительную величину e: .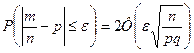

Задача 8. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число e, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала e.

Решение. В этом примере p=0,8, n=400. По условию задачи 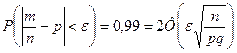. Следовательно, 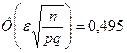, По таблице для функции Лапласа определяем 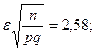и значит, e=0,0516.

 

Приближенную формулу можно использовать и в следующей «урновой» схеме: из генеральной совокупности объема N, содержащей М белых и N-M черных шаров, осуществляется последовательный выбор без возвращения n элементов. Вероятность того, что в полученной выборке окажется ровно m белых шаров, вычисляется по формуле

P_M,N(m,n)= .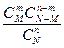

Если объем генеральной совокупности и число белых шаров достаточно велики (N®¥, M®¥, M/N®p=const), то «урновую» схему можно приближенно заменить схемой Бернулли:

P_M,N(m,n)»P_n(m), где P_n(m)=C_n^mp^mq^n-m

Полиномиальные испытания

От схемы независимых последовательных испытаний с двумя исходами (схема Бернулли или биномиальная схема) можно перейти к полиномиальной схеме, то есть к схеме последовательных независимых испытаний, в каждом из которых возможны k исходов, k>2, с вероятностями p₁,p₂,…,p_k, 0<p_i<1, 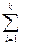p_i=1. В этом случае пространство элементарных событий содержит kⁿ таких событий, а вероятность того, что из n испытаний m₁ закончатся первым исходом, m₂ – вторым исходом,…, m_k – k-м исходом равна

P_n(m₁,…,m_k) = .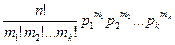

Полученная формула носит название полиномиального закона распределения.

 

Задача 9. Шесть рукописей раскладываются случайным образом в пять папок. Какова вероятность, что ни одна папка не останется пустой?

Решение. На раскладку 6 рукописей в папку можно смотреть на серию шести полиномиальных испытаний с 5 исходами (попадание в i-ую папку – это i-ый исход). Вероятности исходов (папок) совпадают и равны 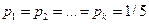. Событие A=«ни одна папка не останется пустой» означает, что в одну папку попадут 2 рукописи, а в остальные папки – по одной рукописи. Следовательно, вероятность того, что в первую папку попадут 2 рукописи, а в остальные папки – по одной рукописи, равна

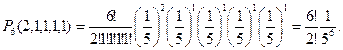
а вероятность искомого события A (для которого неважно, в какую из 5 папок попадают две рукописи) равна