Равнобедренные треугольники

Многоугольники

1. Сумма трех углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 300°. Най­ди­те чет­вер­тый угол. Ответ дайте в градусах.

2. В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD , , , 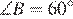. Най­ди­те угол A. Ответ дайте в градусах.

3. Углы вы­пук­ло­го че­ты­рех­уголь­ни­ка от­но­сят­ся как 1:2:3:4. Най­ди­те мень­ший угол. Ответ дайте в градусах.

4. Два угла впи­сан­но­го в окруж­ность че­ты­рех­уголь­ни­ка равны 82° и 58°. Най­ди­те боль­ший из остав­ших­ся углов. Ответ дайте в градусах.

5. Четырёхугольник ABCD впи­сан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Най­ди­те угол ABD. Ответ дайте в градусах.

6. ABCDEFGH — пра­виль­ный восьмиугольник. Най­ди­те угол EFG. Ответ дайте в градусах.

7.

Радиус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

8. Сторона AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окружности. Най­ди­те ∠ C, если ∠ A = 75°. Ответ дайте в градусах.

9. В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD AB = BC, AD = CD, ∠ B = 77°, ∠ D = 141°. Най­ди­те угол A. Ответ дайте в градусах.

10.

Сторона треугольника проходит через центр описанной около него окружности. Найдите 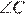, если . Ответ дайте в градусах.

Параллелограмм

1. Диагональ BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 65° и 50°. Най­ди­те мень­ший угол параллелограмма.

2. Разность углов, при­ле­жа­щих к одной сто­ро­не параллелограмма, равна 40°. Най­ди­те мень­ший угол параллелограмма. Ответ дайте в градусах.

3. Один угол па­рал­ле­ло­грам­ма в два раза боль­ше другого. Най­ди­те мень­ший угол. Ответ дайте в градусах.

4.

Диагональ AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 30° и 45°. Най­ди­те боль­ший угол параллелограмма.

5.

Диагональ BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 50° и 85°. Най­ди­те мень­ший угол параллелограмма.

6.

В па­рал­ле­ло­грам­ме ABCD про­ве­де­на диа­го­наль AC. Угол DAC равен 47°, а угол CAB равен 11°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD. Ответ дайте в градусах.

7. Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 25° и 30°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма.

8. 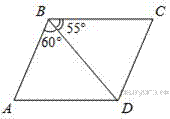Диа­го­наль BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 60° и 55°. Най­ди­те мень­ший угол па­рал­ле­ло­грам­ма.

9. Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 35° и 30°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма.

10. На про­дол­же­нии сто­ро­ны AD па­рал­ле­ло­грам­ма ABCD за точ­кой D от­ме­че­на точка E так, что DC = DE. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD, если ∠ DEC = 53°. Ответ дайте в градусах.

11. В па­рал­ле­ло­грамм впи­са­на окруж­ность. Най­ди­те пе­ри­метр па­рал­ле­ло­грам­ма, если одна из его сто­рон равна 6.

12. В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и ∠ ACD = 104°. Най­ди­те угол между диа­го­на­ля­ми параллелограмма. Ответ дайте в градусах.

13. Найдите ве­ли­чи­ну остро­го угла па­рал­ле­ло­грам­ма ABCD, если бис­сек­три­са угла A об­ра­зу­ет со сто­ро­ной BC угол, рав­ный 15°. Ответ дайте в градусах.

14. Найдите острый угол параллелограмма , если биссектриса угла 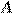образует со стороной угол, равный 33°. Ответ дайте в градусах.

15.

Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 31°. Ответ дайте в градусах.

16.

В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

17.

Найдите величину острого угла параллелограмма , если биссектриса угла образует со стороной угол, равный 14°. Ответ дайте в градусах.

18.

Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 41°. Ответ дайте в градусах.

19.

В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

20.

В параллелограмме диагональ в 2 раза больше стороны и . Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

21. Найдите ве­ли­чи­ну остро­го угла па­рал­ле­ло­грам­ма ABCD, если бис­сек­три­са угла A об­ра­зу­ет со сто­ро­ной BC угол, рав­ный 13°. Ответ дайте в градусах.

22. В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и ∠ ACD = 17°. Най­ди­те угол между диа­го­на­ля­ми параллелограмма. Ответ дайте в градусах.

23.

В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и ∠ ACD = 63°. Най­ди­те угол между диа­го­на­ля­ми параллелограмма. Ответ дайте в градусах.

24. Биссектриса угла A па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ет сто­ро­ну BC в точке K. Най­ди­те пе­ри­метр параллелограмма, если BK = 6, CK = 10.

Равнобедренные треугольники

1.

В рав­но­сто­рон­нем тре­уголь­ни­ке ABC бис­сек­три­сы CN и AM пе­ре­се­ка­ют­ся в точке P. Найдите .

2.

В рав­но­бед­рен­ном треугольнике . Най­ди­те , если вы­со­та .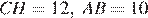

3. 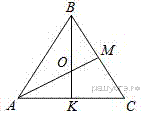В рав­но­сто­рон­нем тре­уголь­ни­ке ABC ме­ди­а­ны BK и AM пе­ре­се­ка­ют­ся в точке O. Най­ди­те .

4. Пло­щадь рав­но­бед­рен­но­го тре­уголь­ни­ка равна Угол, ле­жа­щий на­про­тив ос­но­ва­ния равен 120°. Най­ди­те длину бо­ко­вой сто­ро­ны.

5. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 196, а ос­но­ва­ние — 96. Най­ди­те пло­щадь тре­уголь­ни­ка.

6.

В тре­уголь­ни­ке ABC AC = BC. Внеш­ний угол при вер­ши­не B равен 146°. Най­ди­те угол C. Ответ дайте в градусах.

7. Точка D на сто­ро­не AB тре­уголь­ни­ка ABC вы­бра­на так, что AD = AC. Известно, что ∠ CAB = 80° и ∠ ACB =59∘. Най­ди­те угол DCB. Ответ дайте в градусах.

8.

Высота рав­но­сто­рон­не­го тре­уголь­ни­ка равна Най­ди­те его периметр.

9.

В тре­уголь­ни­ке ABC AB = BC = 53, AC = 56. Най­ди­те длину ме­ди­а­ны BM.

10. Боковая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 10, а ос­но­ва­ние равно 12. Най­ди­те пло­щадь этого треугольника.

11.

В треугольнике известно, что , . Найдите угол 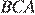. Ответ дайте в градусах.

12.

В треугольнике известно, что , . Найдите угол 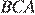. Ответ дайте в градусах.

13. 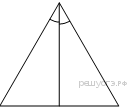Сторона равностороннего треугольника равна 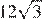. Найдите биссектрису этого треугольника.

14.

Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

15. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.

16. В треугольнике известно, что , . Найдите угол 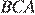. Ответ дайте в градусах.

17. В треугольнике известно, что , . Найдите угол 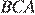. Ответ дайте в градусах.

18. Биссектриса равностороннего треугольника равна 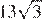. Найдите сторону этого треугольника.

19. В треугольнике известно, что , 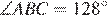. Найдите угол 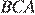. Ответ дайте в градусах.

20. Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.

21. Сторона равностороннего треугольника равна . Найдите медиану этого треугольника.

22. Высота равностороннего треугольника равна . Найдите сторону этого треугольника.

23. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.

24. Сторона равностороннего треугольника равна . Найдите биссектрису этого треугольника.

25. В треугольнике известно, что , . Найдите угол 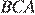. Ответ дайте в градусах.

26. Медиана равностороннего треугольника равна . Найдите сторону этого треугольника.

27. В тре­уголь­ни­ке ABC AC = BC. Внеш­ний угол при вер­ши­не B равен 140°. Най­ди­те угол C. Ответ дайте в градусах.

Ромб

1.

Сто­ро­на ромба равна 34, а ост­рый угол равен 60°. Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

 

Перечислите эти длины в от­ве­те без пробелов в по­ряд­ке возрастания.

2. Пло­щадь ромба равна 27, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.

3. Рас­сто­я­ние от точки пе­ре­се­че­ния диа­го­на­лей ромба до одной из его сто­рон равно 19, а одна из диа­го­на­лей ромба равна 76. Най­ди­те углы ромба.

В от­ве­те за­пи­ши­те ве­ли­чи­ны раз­лич­ных углов в по­ряд­ке воз­рас­та­ния без пробелов.

4. Точка O — центр окружности, на ко­то­рой лежат точки P, Q и R таким образом, что OPQR — ромб. Най­ди­те угол ORQ. Ответ дайте в градусах.

5.

Точка O — центр окружности, на ко­то­рой лежат точки S, T и V таким образом, что OSTV — ромб. Най­ди­те угол STV. Ответ дайте в градусах.

6.

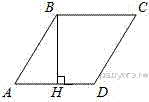
Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.

Трапеция

1. Найдите боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° соответственно.

2. Найдите угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 50° соответственно.

3. Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол трапеции. Ответ дайте в градусах.

4. Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 220°. Най­ди­те мень­ший угол трапеции. Ответ дайте в градусах.

5. Найдите мень­ший угол рав­но­бед­рен­ной трапеции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в градусах.

6. Основания тра­пе­ции равны 4 см и 10 см. Диа­го­наль трапеции делит сред­нюю линию на два отрезка. Най­ди­те длину боль­ше­го из них.

7.

Найдите угол ABC рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной CD углы, рав­ные 30° и 80° соответственно.

8.

Найдите мень­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем BC и бо­ко­вой сто­ро­ной CD углы, рав­ные 30° и 105° соответственно.

9.

Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен 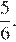Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

10.

Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 40° со­от­вет­ствен­но.

11.

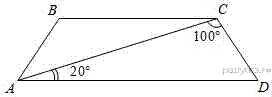
Най­ди­те угол АВС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной CD углы, рав­ные 20° и 100° со­от­вет­ствен­но.

12.

Най­ди­те мень­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной CD углы, рав­ные 30° и 105° со­от­вет­ствен­но.

13.

Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной АВ углы, рав­ные 25° и 40° со­от­вет­ствен­но.

14.

В рав­но­бед­рен­ной тра­пе­ции из­вест­ны вы­со­та, мень­шее ос­но­ва­ние и угол при ос­но­ва­нии. Най­ди­те боль­шее ос­но­ва­ние.

15.

Ос­но­ва­ния тра­пе­ции равны 4 и 10. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

16.

Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

17. Около тра­пе­ции, один из углов ко­то­рой равен 49°, опи­са­на окруж­ность. Най­ди­те осталь­ные углы тра­пе­ции.

Запишите ве­ли­чи­ны углов в ответ без пробелов в по­ряд­ке неубывания.

18. В тра­пе­цию, сумма длин бо­ко­вых сто­рон ко­то­рой равна 24, впи­са­на окруж­ность. Най­ди­те длину сред­ней линии тра­пе­ции.

19. Биссектрисы углов A и B при бо­ко­вой сто­ро­не AB тра­пе­ции ABCD пе­ре­се­ка­ют­ся в точке F. Най­ди­те AB, если AF = 24, BF = 32.

20. В тра­пе­ции ABCD AB = CD, ∠ BDA = 49° и ∠ BDC = 13°. Най­ди­те угол ABD. Ответ дайте в градусах.

21.

Высота рав­но­бед­рен­ной трапеции, проведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 1 и 5. Най­ди­те длину ос­но­ва­ния BC.