Кварто-квинтовый круг тональностей
или просто квинтовый круг - это схема для удобного и быстрого запоминания всех тональностей и ключевых знаков в них.
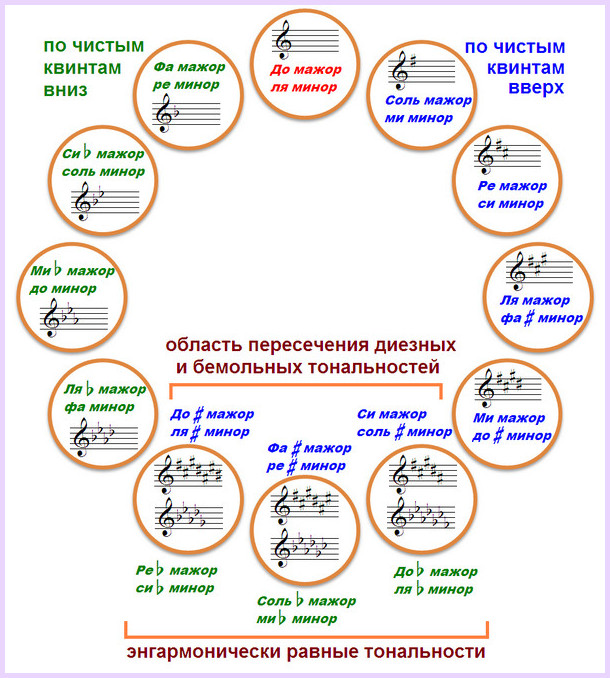
В вершине квинтового круга находится тональность До мажор;
по часовой стрелке - диезные тональности, тоники которых расположены по чистым квинтам вверх от тоники исходного До мажора;
против часовой стрелки - круг бемольных тональностей, расположенных также по чистым квинтам, но только вниз.
При этом, при движении по квинтовому круг по часовой стрелке
с каждой новой тональностью постепенно возрастает количество диезов (от одного до семи),
при движении против часовой стрелки, соответственно, от одной тональности к другой возрастает количество бемолей (также от одного до семи).
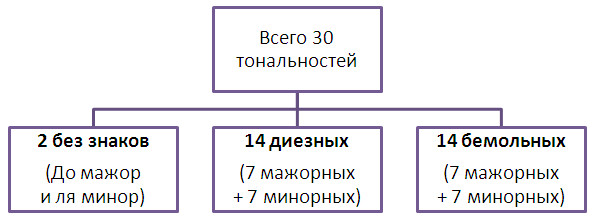
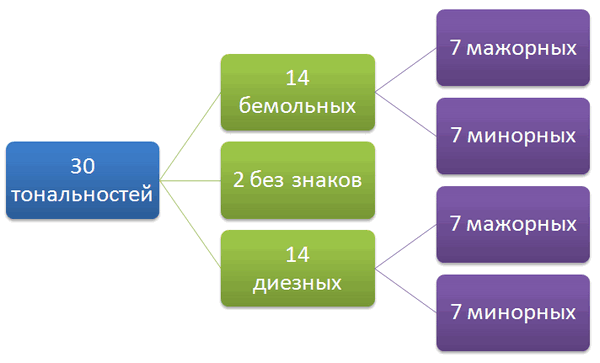
В музыке применяется, главным образом, 30 тональностей,
из которых одна половина – мажорные, а другая – минорные. Мажорные и минорные тональности образуют пары по принципу совпадения в них ключевых знаков альтерации – диезов и бемолей. Тональности с одинаковыми знаками называются параллельными. Всего, таким образом, есть 15 пар параллельных тональностей.
Из 30 тональностей две не имеют знаков – это До мажор и ля минор.
14 тональностей имеют диезы (от одного до семи по порядку диезов ФА ДО СОЛЬ РЕ ЛЯ МИ СИ),
из этих 14 семь тональностей семь будут мажорные, а семь, соответственно, минорные.
Ещё 14 тональностей имеют бемоли (аналогично от одного до семи, но только по порядку бемолей СИ МИ ЛЯ РЕ СОЛЬ ДО ФА), из них также семь мажорных и семь минорных.
Почему называют кварто-квинтовый круг тональностей?
Дело в том, что кварта является обращением интервала квинты. И тот же ряд тональностей круга можно получить если двигаться не по квинтам, а по квартам.
|
|
Например, диезные тональности можно расположить не по чистым квинтам вверх, а по чистым квартам вниз. Получится тот же самый ряд:
Бемольные тональности можно расположить не по чистым квинтам вниз, а по чистым квартам вверх. И снова результат будет один и тот же:
Для чего необходимо знать кварто-квинтовый круг?
Для того, чтобы не считать тона и полутона каждый раз для получения верной гаммы, а знать конкретно и сразу, какие звуки будут понижены или повышены в данной гамме. Соль мажор — 1 диез, значит играем от СОЛЬ до СОЛЬ через фа-диез.
А самое важное применение кварто-квинтового круга – транспозиция .(перенос мелодии на новую высоту) Иногда возникают ситуации, когда вы хотите спеть песню под фортепиано, но её тональность не подходит под ваш голосовой диапазон.И зная тональности и ключевые знаки,вы без труда можете перенести любимую песню в удобную для вашего диапазона тональность. 
Тональность - это высотное положение лада, построенного от определенной ноты.
Другими словами: тональность – это высота звучания музыкального произведения, которая определяется тоникой.
Параллельные тональности – это мажорная и минорная тональность, которые имеют разную тонику, но содержат одинаковый набор нот и ключевых знаков.
Т.Е параллельными называются мажорная и минорная тональности, у которых одинаковые ключевые знаки, общие звуки, но разные тоники. Например: До-мажор и ля-минор; Соль-мажор и ми-минор; Фа-мажор и ре-минор; Ре-мажор и си-минор; СиЬ-мажор и соль минор.
|
|
Разница между тониками параллельных тональностей равна малой терции. 
Одноименными тональностями называются мажорная и минорная тональности, имеющие общую тонику, но разные ключевые знаки. Например: До мажор (нет знаков) и до минор (сиЬ, миЬ, ляЬ). Разница в ключевых знаках всегда равна трем.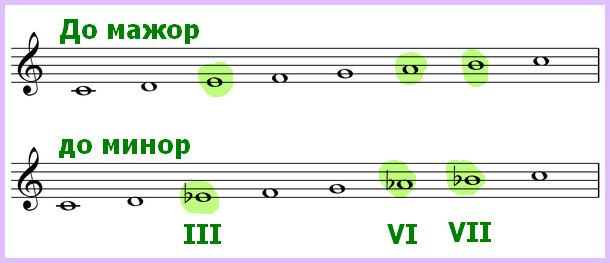 
Кстати, квинтовый круг нельзя строго назвать кругом, он представляет собой скорее некое подобие спирали, так как на определённом этапе некоторые тональности пересекаются из-за совпадения по высоте звучания.
Энгармонически равные тональности - это тональности одинаковые по звучанию, но различные по названию и написанию: Си мажор - До-бемоль мажор, Фа-диез мажор - Соль-бемоль мажор.