Тема: Работа силы. Мощность
Понятие работы
Работа силы – физическая величина, характеризующая результат действия силы.
Механическая работа А постоянной силы 
равна произведению модуля вектора силы на модуль вектора перемещения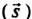 
и на косинус угла а между вектором силы и вектором перемещения:
А = Fs cos а.
Единица измерения работы в СИ – джоуль: [А] = Дж = Н • м.
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.
Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:
· сила действует, а тело не перемещается;
· тело перемещается, а сила равна нулю;
· угол между векторами силы и перемещения равен 90° (cos a = 0).
Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости.
Работа – скалярная величина, она может быть как положительной, так и отрицательной.
1. Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
2. Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.
Работа обладает свойством: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.
Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: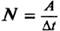 
.
Мощность показывает, какая работа совершается за 1 с.
Единица измерения мощности в СИ – ватт: [ N ] = Дж/с = Вт.
Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.
|
|
Может пригодиться! 1 л. с. (лошадиная сила) ~ 735 Вт.
Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим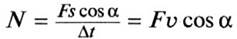 
.
Для равноускоренного движения (F = const)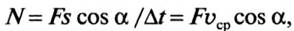 
где ʋср – средняя скорость движения за расчётный промежуток времени.
Вертикальное движение тела под действием силы тяжести
При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна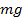 
, где m – масса тела, g – ускорение свободного падения.
Пусть тело массой m свободно падает с высоты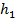 
над каким-либо уровнем, с которого ведётся отсчёт, до высоты 
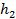над тем же уровнем (см. Рис. 1).
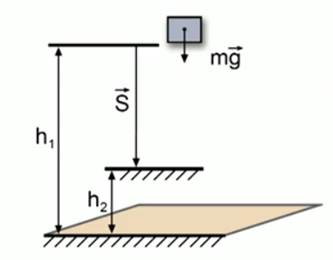
Рис. 1. Свободное падение тела с высоты 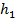до высоты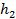
При этом модуль перемещения тела равен разности этих высот:
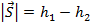
Так как направление перемещения и силы тяжести совпадают, то работа силы тяжести равна:
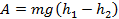
Значение высот в этой формуле можно отсчитывать от любого уровня (уровень моря, уровень дна ямы, которая вырыта в земле, поверхность стола, поверхность пола и т. д.). В любом случае высоту данной поверхности выбирают равной нулю, поэтому уровень данной высоты называют нулевым уровнем.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести будет равна:
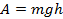
Если тело, брошенное вверх с нулевого уровня, достигает высоты h над этим уровнем, то работа силы тяжести будет равна:
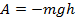
Движение тела по прямолинейной траектории, наклонённой под некоторым углом к горизонту
|
|
Пусть тело массой m движется по наклонной плоскости высотой h и при этом совершает перемещение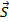 
, модуль которого равен длине наклонной плоскости (см. Рис. 2).
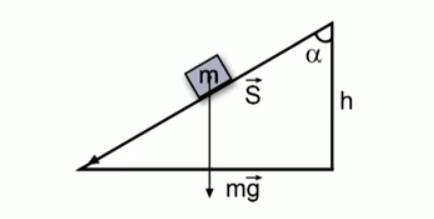
Рис. 2. Движение тела по наклонной плоскости
Работа силы равна скалярному произведению вектора силы на вектор перемещения тела, совершённого под действием данной силы, то есть работа сила тяжести в данном случае будет равна:
,
где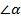 
– угол между векторами силы тяжести и перемещения.
На рисунке 2 видно, что перемещение (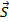) представляет собой гипотенузу прямоугольного треугольника, а высота h – катет. Согласно свойству прямоугольного треугольника:
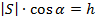
Следовательно
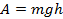
Работа силы тяжести при движении тела по криволинейной траектории
Мы получили выражение для работы силы тяжести такое же, как в случае вертикального движения тела. Можно сделать вывод: если траектория тела не является прямолинейной и тело движется под действием силы тяжести, то работа силы тяжести определяется только изменением высоты тела над некоторым нулевым уровнем и не зависит от траектории движения тела.
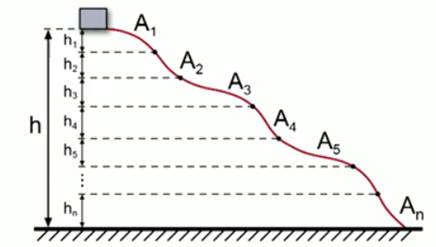
Рис. 3. Движение тела по криволинейной траектории
Докажем предыдущее утверждение. Пусть тело движется по некоторой криволинейной траектории (см. Рис. 3). Эту траекторию мысленно разбиваем на ряд малых участков, каждый из которых можно считать маленькой наклонной плоскостью. Движение тела по всей траектории можно представить как движение по множеству наклонных плоскостей. Работа силы тяжести на каждом из участков будет равна произведению силы тяжести на высоту данного участка. Если изменения высот на отдельных участках равны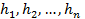 
, то работы силы тяжести на них равны:
|
|
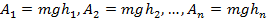
Полная работа на всей траектории равна сумме работ на отдельных участках:
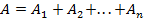
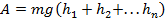
Так как
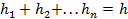– полная высота, которую преодолело тело,
То
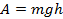
Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. Что и требовалось доказать.
При движении вниз работа положительна, при движении вверх – отрицательна.
Работа силы тяжести при движении тела по замкнутой траектории
Пусть некоторое тело совершило движение по замкнутой траектории, то есть оно сначала спустилось вниз, а потом по какой-то другой траектории вернулось в исходную точку. Так как тело оказалось в той же самой точке, в которой оно было изначально, то разность высот между начальным и конечным положением тела равна нулю, поэтому и работа силы тяжести будет равна нулю. Следовательно, работа силы тяжести при движении тела по замкнутой траектории равна нулю.
Решение задачи на мощность
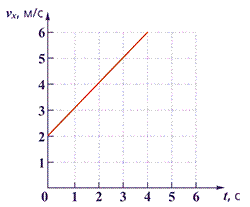
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведён график зависимости проекции скорости vх тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение: по графику проекция скорости в момент времени 3с, равна 5 м/с. Мощность, развиваемая силой F для тела, движущегося со скоростью можно найти по формуле
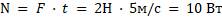
Ответ: 10 Вт
Итоги урока
На данном уроке мы научились вычислять работу, работу силы тяжести. При этом увидели, что, независимо от траектории движении тела, работа силы тяжести определяется разностью между высотами начального и конечного положения тела над некоторым нулевым уровнем. Также мы ввели понятие потенциальной энергии и показали, что работа силы тяжести равна изменению потенциальной энергии тела, взятой с противоположным знаком.
Образцы заданий ЕГЭ
А1. На горизонтальной поверхности находится тело, на которое действуют с силой 10 Н, направленной под углом 60° к горизонту (см. рис). Под действием этой силы тело перемещается по поверхности на 5 м. Работа силы равна
1) 3000 Дж 2) 50 Дж 3) 25 Дж 4) 0
А2. Мальчик тянет санки за верёвку с силой 50 Н. Пройдя с санками 100 м, он совершил работу 2500 Дж. Чему равен угол между верёвкой и дорогой?
1) 90° 2) 45° 3) 60° 4) 30°
АЗ. С помощью динамометра, расположенного под углом 30° к горизонтальной поверхности, равномерно перемещают брусок массой 100 г на расстояние, равное 20 см. Работа равнодействующей всех сил равна
1) 0 2) 0,01 Дж 3) 0,02 Дж 4) 0,03 Дж
А4. Под действием силы тяги 1000 Н автомобиль движется с постоянной скоростью 72 км/ч. Мощность двигателя равна
1) 10 кВт 2) 20 кВт 3) 40 кВт 4) 72 кВт
А5. Какую мощность развивает двигатель подъёмного механизма крана, если он равномерно поднимает плиту массой 600 кг на высоту 4 м за 3 с?
1) 72 000 Вт 2) 8000 Вт 3) 7200 Вт 4) 800 Вт