Конспект занятия
Ребята, я предлагаю сегодня привести в систему знания и расширить представление о равносильности неравенств. Дьёрдь По́йа сказал: «Недостаточно лишь понять задачу, необходимо желание решить её. Где есть желание, найдется путь!» А я уверена, что у вас есть желание узнать новое, анализировать, делать выводы, найти свой путь решения и расширить знания, которые вам понадобятся для успешной сдачи ГИА.
Равносильность неравенств
Выполнение некоторых действий с правой и/или левой частью неравенства или с их отдельными слагаемыми может давать новые неравенства, имеющие те же решения, что и исходное неравенство. Замену исходного неравенства на новое равносильное ему неравенство при помощи таких действий назвали равносильным преобразованиям неравенства. Равносильное преобразование неравенства – это его замена другим равносильным ему неравенством, то есть, неравенством, имеющим то же множество решений. Сами преобразования, приводящие к равносильному неравенству, также называют равносильными преобразованиями.
Возникает логичный вопрос: «Зачем вообще нужны эти равносильные преобразования неравенств»? Например, они позволяют решать неравенства: с их помощью от решения исходного неравенства можно перейти к решению более простого, но равносильного неравенства.
Определение1. Два неравенства с одной переменной f(x)>g(x) и p(x)>h(x) называют равносильными, если их решения совпадают.
Определение2. Если общее решение неравенства f(x)>g(x) содержится в общем решении неравенства p(x)>h(x), то второе неравенство называют следствием первого.
Например
х2>9 –это неравенство - следствие неравенства 2х>6.
2х<6 – следствие неравенства х2<9
Теперь можно перейти к знакомству с основными и наиболее часто используемыми равносильными преобразованиями неравенств, которые иногда называют свойствами неравенств. Им стоит уделить должное внимание – без их использования не обходится решение почти ни одного неравенства. Заметим, что они похожи на равносильные преобразования уравнений. Принцип их доказательства тоже аналогичен, только здесь в основе доказательства будут лежать, естественно, свойства числовых неравенств, а не свойства числовых равенств.
Итак, приступим.
Теорема1. Если какой-либо член неравенства перенести из одной части неравенства в другую с противоположным знаком, оставив знак неравенства без изменения, то получится неравенство, равносильное данному неравенству.
f(x)>g(x)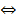 
f(x) - g(x)>0
Прибавление (или вычитание) из обеих частей неравенства одного и того же числа является равносильным преобразованием. К примеру, оно позволяет от неравенства 3x>12+5х перейти к равносильному неравенству 3x – 5х>12.
Теорема 2. Если обе части неравенства возвести в одну и ту же нечетную степень, оставив знак неравенства без изменения, то получится неравенство равносильное данному.
f(x)>g(x) 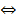(f(x))2n-1 > (g(x))2n-1
Пример: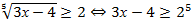 
Теорема 3. Показательное неравенство аf(x) >аg(x) равносильно:
а) неравенству того же смысла f(x)>g(x), если а>1,
б) неравенству противоположного смысла f(x)<g(x), если 0<а<1
аf(x) >аg(x) 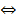f(x)>g(x), если а>1 и аf(x) >аg(x) 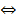f(x)<g(x), если 0<а<1
Примеры: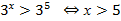 
и 
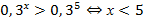
Теорема4.
а)Если обе части неравенства f(x)>g(x) умножить на одно и то же выражение h(x), положительное при всех х из области определения неравенства f(x)>g(x), оставив при этом знак неравенства без изменения, о получится неравенство f(x) h(x)>g(x) h(x), равносильное данному.
б) Если обе части неравенства f(x)>g(x) умножить на одно и то же выражение h(x), отрицательное при всех х из области определения неравенства f(x)>g(x), изменив при этом знак неравенства на противоположный, то получится неравенство f(x) h(x)<g(x) h(x), равносильное данному.
Если h(x)>0 на ОДЗ неравенства f(x)>g(x), то f(x)>g(x)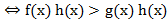 
Если h(x)<0 на ОДЗ неравенства f(x)>g(x), то f(x)>g(x)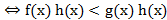 
Примеры: 2х>4 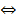х>2 и х(-х2-1) >-х2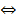-1 х<1
Теорема5. Если обе части неравенства f(x)>g(x) неотрицательны в области его определения, то после возведения обеих частей неравенства в одну и ту же четную степень получится неравенство того же смысла (f(x))2n > (g(x))2n, равносильное данному в его ОДЗ.
Если f(x)≥0 и g(x)≥0, то f(x)>g(x)⇔ (f(x))2n > (g(x))2n
Пример: х2≥9⇔х≥3 при х≥0
Теорема 6. Пусть Х – решение системы неравенств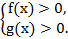 
Тогда логарифмическое неравенство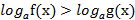 
равносильно на множестве Х:
а) неравенству того же смысла f(x)>g(x), если а>1,
б) неравенству противоположного смысла f(x)<g(x), если 0<а<1.
Пример: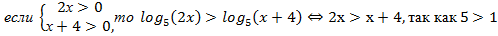 
,
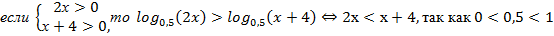
Замена выражения в левой и/или правой части неравенства тождественно равным выражением на области допустимых значений (ОДЗ) переменных исходного неравенства является равносильным преобразованием неравенства.
Отдельно подчеркнем важность учета ОДЗ при замене частей неравенства тождественно равными им выражениями: если ОДЗ полученного неравенства будет отличаться от ОДЗ исходного неравенства, то это неравенство может быть не равносильно исходному. Этот момент критически важен, он может приводить к неверным ответам при решении неравенств. Не менее важен и момент, касающийся замены на именно тождественно равное выражение
К чему приводят неравносильные преобразования неравенств?
Возьмем неравенства
1) x>−2 и -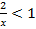 
. Решением первого является промежуток (−2, +∞), а второго – (-∞; -2) 
.
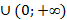2) 
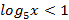и х<5. Решением первого является промежуток (0; 5), а второго – (-∞; 5)
Вывод: Признаком возможного неравносильного преобразования неравенства является сужение или расширение ОДЗ. Наиболее часто неравносильные переходы при решении неравенств возникают при неаккуратном применении свойств корней, логарифмов и модуля. На этом мы особо заострим внимание, когда будем разбираться с решением неравенств соответствующих видов
Решим неравенство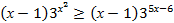 
, применяя теоремы равносильности
Ответ: [1; 2]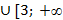 
)