Производная и ее приложения
Понятие производной
 Пусть функция y = f (x) определена на множестве X. Выберем произвольную точку x Î X и придадим значению x приращение Δ x, тогда функция y = f (x) получит приращение Δ y=f (x +Δ x)– f (x), определяемое как разность наращенного и исходного значений функции. Производной функции y = f (x) в точке x называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю (если этот предел существует), т.е. y '=
Пусть функция y = f (x) определена на множестве X. Выберем произвольную точку x Î X и придадим значению x приращение Δ x, тогда функция y = f (x) получит приращение Δ y=f (x +Δ x)– f (x), определяемое как разность наращенного и исходного значений функции. Производной функции y = f (x) в точке x называется предел отношения приращения функции к приращению аргумента при стремлении его к нулю (если этот предел существует), т.е. y '=  . Различные обозначения производной: y ';
. Различные обозначения производной: y ';  (x);
(x);  . Кроме того, иногда в качестве нижнего индекса указывается аргумент, по которому берется производная: y ' x;
. Кроме того, иногда в качестве нижнего индекса указывается аргумент, по которому берется производная: y ' x;  x (x).
x (x).
С геометрической точки зрения производная функции y = f (x) в точке x 0 есть тангенс угла наклона касательной к графику функции в этой точке.т.е. f (x 0)=tg α= k.
С механической точки зрения производная пути материальной точки по времени в точке t 0 есть ее скорость в этот момент времени, т.е. v (t 0)= S '(t 0).
Если функция y = f (x) имеет в точке x конечную производную, то она называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке.
Справедлива теорема о связи между непрерывностью и дифференцируемостью функции: если функция y = f (x) дифференцируема в точке x 0, то она непрерывна в этой точке. Обратное, вообще говоря, неверно.
Замечание Производная непрерывной функции не обязательно непрерывна. Если функция имеет на некотором промежутке X непрерывную производную, то функцию называют гладкой на этом промежутке. Если производная функции на промежутке допускает конечное число разрывов первого рода, то функцию называют кусочно-гладкой.
Вычисление производной
Вычисление производной функции y = f (x) может быть выполнено по определению. Для этого:
- задаем приращение аргумента Δ x и вычисляем соответствующее ему значение функции f (x +Δ x);
- вычисляем приращение функции Δ y=f (x +Δ x)– f (x);
- составляем отношение приращения функции к приращению аргумента Δ y /Δ x;
- находим предел этого отношения при Δ x →0, т.е.
 Δ y /Δ x = y '.
Δ y /Δ x = y '.
Производная обладает следующими свойствами, которые удобно использовать для ее вычисления. Пусть C – константа, u = u (x) и v = v (x) – дифференцируемые функции аргумента x.
| Производная константы равна нулю | C '=0 | |
| Производная аргумента равна единице | x '=1 | |
| Производная алгебраической суммы конечного числа функций равна алгебраической сумме производных этих функций | (u ± v)' =u '± v ' |
| Производная произведения конечного числа дифференцируемых функций равна сумме произведений производной каждой из них на все остальные | (u · v · z)' =u '· v · z + u · v '· z + u · v · z ' | |
| 4а | Производная произведения двух дифференцируемых функций равна сумме произведения производной первой из них на вторую и производной второй из них на первую | (u · v)' =u '· v + u · v ' |
| 4б | Постоянный множитель можно выносить за знак производной | (C · u)' =C · u ' |
| Производная частного двух дифференцируемых функций определяется по формуле | 
| |
| Пусть y = f (u), u = φ (x), тогда y = f (φ (x)) – сложная функция. Если y = f (u), u = φ (x) – дифференцируемые функции своих аргументов, то производная сложной функции существует и определяется по формуле | (f (φ (x)))'= f '(φ (x))· φ '(x) |
Производные основных элементарных функций приведены в таблице.
Таблица – Производные основных элементарных функций
| № | Функция | Производная | № | Функция | Производная |
| C | cos x | –sin x | |||
| xn | n · xn–1 | tg x | 1/cos2 x | ||
| ex | ex | ctg x | –1/sin2 x | ||
| ax | ax ·ln a | arcsin x |  , | x |<1 , | x |<1
| ||
| ln x | 1/ x | arccos x | 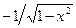 , | x |<1 , | x |<1
| ||
| loga x | 
| arctg x | 
| ||
| sin x | cos x | arcctg x | 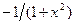
|
Замечание Если функция задана неявно уравнением F (x, y)=0, то для нахождения производной необходимо продифференцировать обе части уравнения по x, рассматривая y как функцию x, и выразить из полученного уравнения y '. Например, если x 2+ y 2=2, то по правилам нахождения производной (x 2+ y 2)'=2', откуда 2 x +2 y · y '=0 и y '=–2 x /2 y.
Дифференциал функции
Пусть функция y = f (x) определена на промежутке X и дифференцируема в некоторой окрестности точки x 0.Тогда в этой точке существует конечная производная y '=  . На основании теоремы о связи бесконечно малых величин с пределами функций
. На основании теоремы о связи бесконечно малых величин с пределами функций 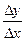 = y '+α(Δ x) при Δ x →0, откуда Δ y=y '·Δ x +α(Δ x) Δ x, где α(Δ x) – бесконечно малая величина при Δ x →0.
= y '+α(Δ x) при Δ x →0, откуда Δ y=y '·Δ x +α(Δ x) Δ x, где α(Δ x) – бесконечно малая величина при Δ x →0.
Дифференциалом функции y = f (x) dy называется линейная относительно Δ x часть приращения функции, равная произведению ее производной y ' на приращение независимой переменной Δ x, т.е. dy = y '·Δ x. При этом для функции y = x dy = dx = x '·Δ x =1·Δ x =Δ x, т.е dx =Δ x Тогда выражение для дифференциала в общем виде перепишется как dy = y '· dx = f '(x)· dx.
Свойства дифференциала аналогичны свойствам производной. Пусть C – константа, u = u (x) и v = v (x) – дифференцируемые функции аргумента x. Тогда
1 dC =0
2 d (C · u)= C · du
3 d (u ± v) =du ± dv
4 d (u · v) = v · du + u ·d v
5 
6 Инвариантность формы дифференциала. Пусть y = f (u), u = φ (x), тогда dy = f '(φ (x))· φ '(x) dx.
Производные и дифференциалы высших порядков
Поскольку производная f '(x) сама является функцией, то она так же может иметь производную. Тогда производной n -го порядка называют производную от производной
(n –1)-го порядка. Таким образом, f ''(x) – производная II порядка; f'''(x) – производная III порядка, … f ( n )(x) – производная n -го порядка.
С механической точки зрения вторая производная пути материальной точки по времени ест ее ускорение.
Для дифференцируемой функции y = f (x) ее дифференциал имеет вид dy = f '(x)· dx.
Тогда дифференциалом второго порядка (или вторым дифференциалом) функции y = f (x) называется дифференциал от ее дифференциала первого порядка, т.е. d 2 y = d (dy)= d (f '(x)· dx)=dx · d (f '(x))= dx · f ''(x)· dx = f ''(x)· dx 2.
Аналогично дифференциалом n -го порядка (или n -ым дифференциалом) y = f (x) называется дифференциал от ее дифференциала (n –1)-го порядка, т.е. dny = d (dn – 1 y)= f ( n )(x)· dxn.