МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Контрольные работы
для студентов
заочной формы обучения
Псков
2015
ОБЩИЕ ПОЛОЖЕНИЯ
Контрольная работа по математическому анализу
для студентов заочного отделения всех специальностей,
охватывает следующие разделы:
1. Пределы и непрерывность;
2. Дифференциальное исчисление функции одной переменной;
3. Интегральное исчисление функции одной переменной;
4. Дифференциальные уравнения;
5. Функции нескольких переменных.
6. Числовые ряды.
При выполнении контрольных работ следует использовать литературу, указанную в данном пособии.
Контрольную работу следует выполнять в отдельной тетради, используя синие или черные чернила.
Перед каждой задачей необходимо выписать ее условие, а после решения - ответ.
Решение каждой задачи должно сопровождаться необходимыми пояснениями.
СПИСОК РЕКОМЕНДУЕМОЙ УЧЕБНОЙ ЛИТЕРАТУРЫ
1. Высшая математика для экономистов.: Учебник / Под ред.
Кремера Н.Ш. - М: ЮНИТИ - ДАНА, 2000 (2001, 2008).
2. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. – М.: Дело, 2003).
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.: Учебное пособие. В 2-х частях. - М.: Высшая школа, 1999 (2006).
4. Сборник задач по высшей математике для экономистов. Учебное пособие. / Ермаков В.И. - М: ИНФРА-М, 2001 (2007, 2009).
5. Высшая математика для экономистов. Практикум / Под ред.
Кремера Н.Ш. - М: ЮНИТИ, 2007.
Задание 1.
Найти пределы функции, не пользуясь правилом Лопиталя.
 1.а)
1.а)  б)
б) 
 в)
в)  г)
г) 

 2.а)
2.а)  б)
б) 
 в)
в) 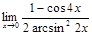 г)
г) 
 3.а)
3.а)  б)
б) 
 в)
в)  г)
г) 
 4.а)
4.а)  б)
б) 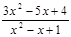
 в)
в)  г)
г) 
 5.а)
5.а)  б)
б) 
 в)
в)  г)
г) 
 6.а)
6.а)  б)
б) 
 в)
в)  г)
г) 

 7.а)
7.а) 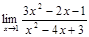 б)
б) 
 в)
в)  г)
г) 
 8.а)
8.а)  б)
б) 
 в)
в) 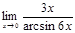 г)
г) 

 9.а)
9.а) 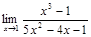 б)
б) 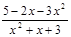
 в)
в)  г)
г) 
 10.а)
10.а)  б)
б) 

 в) г)
в) г) 
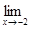
 11.а)
11.а)  б)
б) 
 в)
в) 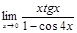 г)
г) 

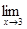 12.а)
12.а)  б)
б) 
 в)
в)  г)
г) 
 13.а)
13.а)  б)
б) 
 в)
в)  г)
г) 
 14.а)
14.а)  б)
б) 

 в) г)
в) г) 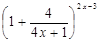
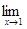 15.а)
15.а)  б)
б) 
 в)
в) 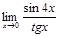 г)
г) 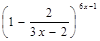
 16.а)
16.а)  б)
б) 
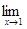 в)
в)  г)
г) 
 17.а)
17.а) 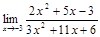 б)
б) 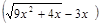
 в)
в)  г)
г) 
 18.а)
18.а)  б)
б) 
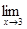 в)
в)  г)
г) 
 19.а)
19.а)  б)
б) 
 в)
в)  г)
г) 
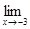 20.а)
20.а)  б)
б) 
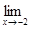 в)
в) 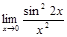 г)
г) 
Задание 2
Найти производные функций, пользуясь формулами дифференцирования.
1. a) 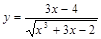 б)
б) 
в)  г)
г) 
2. a) 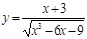 б)
б) 
в)  г)
г) 
3. a)  б)
б) 
в)  г)
г) 
4. a) 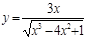 б)
б) 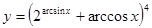
в)  г)
г) 
5. a) 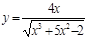 б)
б) 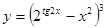
в) 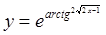 г)
г) 
6. a)  б)
б) 
в)  г)
г) 
7. a)  б)
б) 
в)  г)
г) 
8. a) 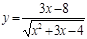 б)
б) 
в)  г)
г) 
9. a)  б)
б) 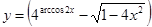
в)  г)
г) 
10. a)  б)
б) 
в)  г)
г) 
11. a)  б)
б) 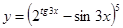
в)  г)
г) 
12. a)  б)
б) 
в) 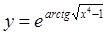 г)
г) 
13. a)  б)
б) 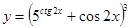
в)  г)
г) 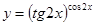
14. a) 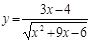 б)
б) 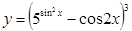
в) 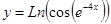 г)
г) 
15. a)  б)
б) 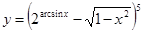
в)  г)
г) 
16. a)  б)
б) 
в)  г)
г) 
17. a)  б)
б) 
в)  г)
г) 
18. a)  б)
б) 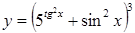
в)  г)
г) 
19. a)  б)
б) 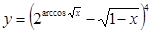
в)  г)
г) 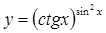
20. a)  б)
б) 
в)  г)
г) 
Задание 3
Провести полное исследование функции методами дифференциального исчисления и построить ее график.
| Вариант | Функция | Вариант | Функция |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
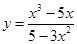
| 
| ||

| 
| ||

| 
| ||

| 
|
1. Найти неопределенный интеграл (табл. 1).
2. Вычислить определенный интеграл (табл. 2).
3. Вычислить площадь фигуры, ограниченной линиями (табл.3).
4. Найти частные производные первого порядка функции нескольких переменных (табл. 4).
5. Найти экстремумы функции двух переменных (табл. 5).
6. Исследовать сходимость числовых рядов (табл. 6).
7. Найти интервал сходимости степенного ряда 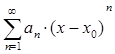 (табл. 7).
(табл. 7).
Таблица 1. Варианты задания
| Вариант | Интеграл | Вариант | Интеграл |


| 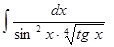

| ||


| 

| ||


| 
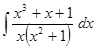
| ||


| 

| ||


| 

| ||


| 

| ||


| 

| ||
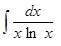

| 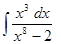
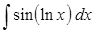
| ||

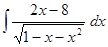
| 

| ||

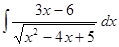
| 
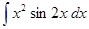
| ||


| 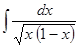

| ||


| 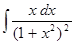

| ||


| 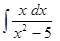

| ||


| 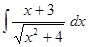

| ||

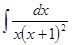
| 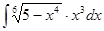

|
Таблица 2. Варианты задания
| Вариант | Интеграл | Вариант | Интеграл |

| 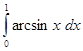
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
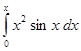
| 
| ||

| 
| ||

| 
| ||

| 
| ||
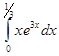
| 
|
Таблица 3. Варианты задания
| Вариант | Уравнения линий | Вариант | Уравнения линий |

| 
| ||

| 
| ||

| 
| ||

| 
| ||
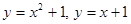
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
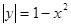
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Таблица 4. Варианты задания
| Вариант | Функция | Вариант | Функция |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
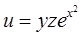
| 
| ||

| 
| ||
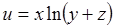
| 
| ||

| 
| ||

| 
| ||

| 
|
Таблица 5. Варианты задания.
| Вариант | Функция | Вариант | Функция |

| 
| ||

| 
| ||

| 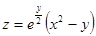
| ||

| 
| ||

| 
| ||

| 
| ||
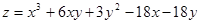
| 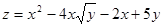
| ||
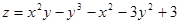
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
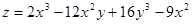
| 
| ||

| 
|
Таблица 6. Варианты задания
| Вариант | Числовой ряд | Вариант | Числовой ряд |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 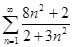
| ||
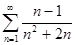
| 
| ||

| 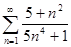
| ||

| 
| ||

| 
| ||

| 
|
Таблица 7. Варианты задания
| Вариант | Числовой ряд | Вариант | Числовой ряд |

| 
| ||
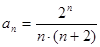
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
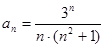
| 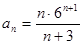
| ||

| 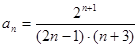
|
ВОПРОСЫК ЭКЗАМЕНУ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
1. Понятие функции. Ее основные свойства. Способы задания функций. Обратная функция. Сложная функция.
2. Предел функции в точке и в бесконечности. Геометрический смысл предела функции в точке и в бесконечности. Бесконечно малые величины. Связь бесконечно малых величин с пределом функции. Свойства бесконечно малых величин. Бесконечно большие величины.
3. Основные теоремы о пределах. Замечательные пределы.
4. Непрерывные функции. Действия над ними. Теорема Вейерштрасса и теорема Коши.
5. Производная функции. Ее механический, экономический и геометрический смысл. Основные правила дифференцирования. Производная сложной функции. Логарифмическое дифференцирование. Производные высших порядков.
6. Приложения производной. Теоремы Ферма, Роля, Лагранжа; их геометрический смысл. Правило Лопиталя. Возрастание и убывание функции. Необходимое и достаточное условия локального экстремума. Выпуклость и вогнутость функции. Точки перегиба. Необходимое и достаточное условия перегиба. Исследование графика функции. Ряды Тейлора и Маклорена.
7. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.
8. Методы интегрирования (метод разложения, метод подстановки, метод интегрирования по частям). Интегрирование рациональных дробей и некоторых видов иррациональностей. Интегрирование тригонометрических функций.
9. Понятие определенного интеграла, его геометрический и экономический смысл. Свойства определенного интеграла. Формула Ньютона - Лейбница. Несобственные интегралы I и II рода.
10. Применение определенного интеграла для расчета площадей плоских фигур, объемов тел вращения, длины дуги плоской кривой, площади поверхности вращения.
11. Функция нескольких переменных. Основные понятия. Предел и непрерывность. Частные производные. Дифференциал. Производная по направлению. Градиент.
12. Экстремумы функции нескольких переменных (локальные, глобальные, условные).
13. Числовые ряды. Сходимость ряда. Признаки сходимости числовых рядов.
14. Степенные ряды. Область сходимости степенного ряда. Применение рядов в приближенных вычислениях.