ИВАН ШАХПАРОНОВ: «РУКОВОДСТВО К ДЕЙСТВИЮ»
Журнал «Мир непознанного» (№19-22 за 1995 г., №4-5 за 1996 г. Вестник РИА-новости)
Часть 1
В качестве основы взяты журнальные оригиналы статьи (1, 2 части у меня были; 3, 4 части прислал И.М. Шахпаронов), так как на авторском сайте https://chakhparonov.ru/ качество статьи плохое: не отформатирована, текстовая «тарабарщина», части иллюстраций нет или искажены (порезаны). Исправлены авторские ошибки в ссылках и приводимых цитируемых материалах. Некоторые небрежные иллюстрации отредактированы.
Обычно при написании научных статей авторы придерживаются некоторого канонизированного порядка: цель исследования со ссылками на предшественников; решение задачи; описание установки; рассуждения на тему, почему это так, а не иначе; заключение. (Все по линейке с небольшими вариациями и редко-редко где-нибудь проскользнут эмоции, как крик, тонущего в трясине... Что-то вроде истории про банку из-под кофе, поставленную под мишень из углерода на выходе ускорителя, в одной работе американских исследователей. Она им по размерам идеально подходила!) Но сколько ценных наблюдений при этом остается "за бортом". Наверняка каждый исследователь может вспомнить что-то такое, что ни он, да и никто другой, не смог в момент эксперимента объяснить. Эти "что-то" приходилось оставлять на потом, так как это выходило за рамки тематики исследований. В 1994 г. в издательстве "Химия" вышла небольшая книга (ее давно ждала научная общественность) под названием "Шаровая молния в лаборатории''. Там есть глава, написанная мною. Но в силу разных обстоятельств до читателя дошел неполный текст. Выпало то, что я и хочу восстановить этой статьей, - правдивый рассказ о нелегком, полном драматизма пути исследователя, добывающего граммы драгоценного знании. Я старался чтиво сделать не просто занимательным, а для многих полезным - руководство к действию с элементами техники безопасности.
|
|
Вообще за это время набралось много экспериментального материала по разным направлениям естествознания. Особенно впечатляющими были два эксперимента: первый - получение трехмерного, развивающегося в собственном времени, изображения галактики; второй - получение "живого" вещества. Читатель, наверное, обратил внимание на то, что в процессе изложения материала я игнорирую медико-биологическую сторону проблемы. Это не случайно, ибо вопрос этот чрезвычайно серьезный и ему будет посвящена отдельная статья настоящего сборника.
Так вот, зимой 1963 г. я впервые попробовал вращать ЛМ (лист Мебиуса) с тем, чтобы избавиться от эффекта "двух фотоаппаратов". В качестве движителя хорошо подходил электродвигатель переменного тока от швейных машин (мощностью 50 Вт, скоростью вращения 3500 об/мин и напряжением 220 В), который я зажал в химическом штативе. На конец вала был напрессован коллектор с щеткодержателями от другого электродвигателя. В поверхности ЛМ было проделано отверстие. Контакт внутри и снаружи обеспечивали пружинные зажимы. Все это сооружение венчала гайка М3. Конструкция получилась очень компактной, в ней были применены серебряные щетки (единственное усовершенствование) вместо графитовых. Силовое питание было то же - 220 В. Время тренировки ВЧ-током от генератора Тесла тогда уже было установлено - что-то около минуты; если 30 сек, то ничего не получается - ЛМ сгорает и все; если 60 сек. - получается шаровая молния; при 90 сек. и более разряд, как правило, не возникает.
|
|
Тренировка проводилась при вращении. ЛМ слегка прецессировал, по-видимому, из-за недостаточной механической прочности. Помещение при этом не затемнялось, горел электрический свет.
С нетерпением ждали, когда все будет готово. Наконец включили. И... ЛМ исчез вместе с установкой. Пропал и все… Подводящие энергию провода повисшие в воздухе, ни на что не опираясь, вдруг оборвались. И в полнейшей тишине произошло чудо! Внезапно, между установкой и мной возник белый и непрозрачный экран размером приблизительно 1 х 1,5 м, большой осью расположенный перпендикулярно полу. Ощущалось, что экран очень тонкий, по его краям пробегали волны, В следующий момент в экране образовалось овальное отверстие с совершенно ровными краями и абсолютно черное. Это была какая-то глубокая, абсолютная чернота. Потом далеко-далеко (в безмерной дали!) вспыхнула фиолетовая искорка и образовался неяркий фиолетовый шарик величиной с горошину. По отдельным неровностям на шарике было заметно, что он довольно быстро вращается. К тому же каким-то необъяснимым образом чувствовалось, что он обладает фантастической температурой. Но в следующий момент картина изменилась: из шарика вытянулись два диаметрально расположенных лучика-рукава травянисто-зеленого цвета, распушенных на концах. Картина была потрясающе красивая: в глубокой черноте вечности вращалось нечто непонятное, но в высшей степени красивое. Далее вся система претерпела существенные изменения. Лучики изогнулись и вся конструкция, вращаясь с небольшой скоростью, стала похожа на латинскую букву S (рис.1), Первый этап закончился ярчайшей (но не слепящей) вспышкой. В следующую секунду я увидел на месте шарика, лучиков и экрана хорошо сформированную галактику (Еще в детстве я увлекался астрономией, поэтому сразу узнал развернувшуюся передо мной картину).
|
|
| 1 - фиолетовый шар-квазар 2 - зеленые лучи-выбросы 3 - стрелка – направления вращения системы рис.1 |
Представьте себе, что перед вашим изумленным взором величественно вращается галактика "метрового диаметра", причем отчетливо видны крупинки звезд на периферии: красные, желтые, зеленые, но в основном голубые. Центральная часть — раскаленный голубой шар, сформированный из звезд-пылинок. Целые потоки звезд вливались в него и выходили, образуя сложную пространственную картину. Галактика имела классическую структуру, но с одним отличием от существующих: в ней не было пылевых облаков. Иными словами, она была очень молода.
Дальнейшие превращения проходили довольно быстро. Лучики-рукава как-то сразу начали втягиваться в центральный шар и застабилизировались в таком положении, В этот момент наша галактика в точности стала похожа на галактику, находящуюся в южном полушарии под названием "Сомбреро", но опять же без пылевых облаков. А затем остатки рукава быстро втянулись в шар. Шар начал смещаться в сторону от предполагаемого центра вращения, одновременно меняя цвет (здесь я придерживаюсь обиходных терминов, поскольку ни черного, ни белого цветов не существует, так как в первом случае это отсутствие света, а во втором — смесь цветов от красного до фиолетового). Сначала цвет шара стал бело-синим, затем белым, интенсивно черным, прозрачным и, наконец, шар пропал. В этот момент вынырнула из небытия установка с вращающимся ЛМ, раздался взрыв и ЛМ разорвало на куски. При повторении такого же эффекта добиться не удалось. Получился вихрь красного пламени и все. Воспроизведение было необходимым, чтобы первой результат эксперимента (столь ошеломляющий!) не выглядел бредом, галлюцинацией.
Хорошо. В воздухе повтор не удался. А если попробовать в сосуде с водой... Сделали достаточно длинный вал, на него закрепили маленький ЛМ из жести и погрузили все это в жидкость — вазелиновое масло. (Обороты двигателя будут меньше из-за большей вязкости масла. Ничего. Это подходит).
| 1 - электродвигатель 2 - стеклянный сосуд 3 - вал двигателя 4 - вазелиновая масса 5 - галактический вихрь 6 - пузырек разрыва жидкости Рис.2 |
Экспериментальная установка была собрана (рис.2), и мы приступили к воспроизведению недавно наблюдавшегося явления... Мы увидели еще одно чудо. При строго определенной скорости вращения (около 1000 об/мин) в сосуде образовывался совершенно обособленный, с четкими границами вихрь, причем был он точной копией описанной выше галактики, только не светился. Бросал в него кусочки цветных бумажек, можно было проследить сложные замкнутые траектории их движения. Вихрь весь состоял из более элементарных взаимно заузленных струй-вихрей, и прелесть была в том, что вихрь этот можно было наблюдать часами, изучать его со всех сторон, менять режимы.
Аналогичные вихри, но в тонком слое жидкости (вихри Рособи), были получены много позже. Топологические трехмерные, а тем более четырехмерные (ввоздухе) вихри еще никому не удавалось (до нас!) получить. К тому же проблема временами вставала в непривычном ракурсе... Из астрономии известно, что наша галактика делает один оборот за 180 миллионов лет. В нашем случае модель ее сделала 40 - 50 оборотов. Значит, жизнь первичной формы галактики весьма коротка (по астрономическим меркам) и равна 7,2 - 9,0 миллиардов лет. Отметим, что пылевых облаков не наблюдалось. Это свидетельство того, что мы наблюдали первичный этап образования галактики, зарождение квазара, его взрыв, зарождение галактики, ее жизнь и переход в новое состояние. И все это заняло около 3-5-ти минут нашего времени. А в природе-то прошли миллиарды лет. В этом и заключена четырехмерность, открывающая возможность проследить всю историю системы - от момента зарождения до перехода в качественно другое состояние. Почему это так - разговор особый. В будущей статье я подробно разберу этот и многие другие вопросы, связанные с геометрией ЛМ и его работой как неориентированного контура.
Мы же отправимся в 1963 год… проводить эксперимент по изготовлению квазиживого вещества. Тогда нам очень хотелось ухватить гравитацию "за хвост". А как это сделать?
В одном из экспериментов мы уже наблюдали впечатляющий эффект — на базе в 5 метров пучок света при воздействии на него поля ЛМ отклонялся от своего нормального положения на несколько сантиметров! Дискутировали много. Высказывались различные предположения — от рассеяния света на ультразвуке и до гравитации. Решили сделать пучок света видимым, хотя бы на некоторой длине пролетной базы. Нашли длинную двухметровую стеклянную трубку (в факультетской стеклодувке химфака МГУ), сделали из нее тройник, впаяв трубку такого же сечения на половине длины первой. Входной и выходной концы закрыли окошечками из оптического стекла. Саша Гвоздецкий предложил применить раствор флуоресцеина вводе, слегка сдобренный раствором аммиака. Аммиак в виде нашатырного спирта мы взяли из аптечки, а флуоресцеин дал Колесников. Растворили, залили, закрепили. Специально для эксперимента был изготовлен ЛМ такого размера, чтобы входил в трубку диаметром 30 мм (рис. 3). Питание ЛМ осуществлялось от трансформатора Тесла.
|
| рис.3 1 - стеклянная труба; 2 - лист Мебиуса; 3 - раствор флуоресцеина; 4 - осветитель; 5 - зрительная труба; 6 - траектория пучка света; 7 - генератор Тесла. |
Эксперимент начался, как обычно, после занятий со студентами (вечером). В зрительную трубку был хорошо виден концентрированный и почти параллельный пучок света от осветителя в виде светящегося диска на желтом фоне. Если смотреть на трубку сбоку, то наблюдалась изумительная картина: травянисто-зеленый, совершенно прямой пучок на фоне желтоватой жидкости в трубке. Включили ЛМ…, все — одно внимание... Что за чертовщина! По ходу пучка все предметы страшно наэлектризовывались. Длинные искры по 2—3 см (60 — 90 кВ) из окуляра трубки бьют в кончик носа и норовят попасть в глаза. Пришлось заземлиться, помогло. В то же время с пучком света начало твориться что-то неладное. Пучок принял вид ущербной луны, а сбоку стал "горбатым". И в таком виде зафиксировался. Вид пучка сохранился даже тогда, когда ЛМ был удален из установки.
| к ЛМ | 
| 1 - поперечное сечение пучка света, видимое в зрительную трубу. 2 - область пепельного света. рис.4 |
Опыт закончился, но самое интересное и неожиданное ждало нас на следующий день. Дело в том, что я хотел вылить содержимое трубки в раковину, но меня удержали от этого мои товарищи — Саша Гвоздецкий и Игорь Махаев. И не напрасно! На следующий день в литровом стакане с бывшей жидкостью образовалась резиноподобная субстанция. И никаких следов жидкости! Проверили рН среды — среда нейтральная. Я взял тонкий срез вещества и под микроскопом с изумлением увидел удлиненные клетки. Значит, вещество может быть живым. Но не как мы, а как-нибудь по-другому. Решили догадку проверить. Все живое хочет есть. Было лето. Поймали муху и бросили в стакан... Через час муха исчезла, а в глубине субстанции была видна расплывающаяся тушка. Оно съело муху!? Дальше мы не стали ничего исследовать. Не договариваясь, разрезали студень и... спустили его в канализацию. Тем и закончилось наше общение с псевдоживой искусственно созданной субстанцией. Для биологических экспериментов время еще не пришло. Мы об этом тогда не догадывались. Все еще было впереди.
Прежде чем перейти к описанию дальнейших экспериментов и результатов, полученных с помощью ЛМ, уместно рассмотреть следующие вопросы: почему все получается именно так, а не иначе, чего можно ожидать от ЛМ и его производных. Иными словами, настал момент для подробного анализа свойств ЛМ.
Зададимся вопросом — почему ЛМ на низких частотах имеет реактивное сопротивление, равное нулю? Очевидно, на высоких частотах за счет спин-эффекта может появляться распределенное реактивное сопротивление, т.е. "размазанное" по всему ЛМ. Рассмотрим, в каких случаях в радиотехнических устройствах реактивность может быть равна нулю. Рассуждения о том, что на проводящей поверхности ЛМ возможны встречные токи, правомерны, однако они не проясняют картины, а напротив — затемняют ее, так как в этом случае индуктивное сопротивление равно нулю, но зато емкостное максимально. А реактивное сопротивление складывается из индуктивного и емкостного. В первом случае важна сила тока, во втором — потенциал. Все это свидетельствует о том, что причина такого поведения системы гораздо глубже простых представлений.
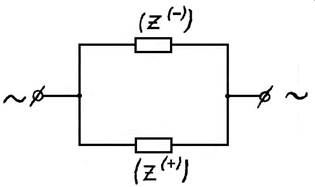
Рис.5
Поскольку ЛМ — замкнутая система с парой контактов (двухполюсник), имеющая нулевое реактивное сопротивление, то предположим, что в общем виде эквивалентная схема имеет вид, представленный на рис.5. Такое предположение можно объяснить следующим образом. Контакты для подвода тока к ЛМ расположены соосно один другому внутри и снаружи. Представим, что при движении в одну сторону от наружного контакта к внутреннему получаем, пускай и незначительное, но одно сопротивление. Продолжая движение в том же направлении, получаем второе сопротивление. Так как начало одного является концом другого, и наоборот, сопротивления в ЛМ включены параллельно. На рис.5 представлены два параллельно включенных сопротивления, причем одно из них должно быть отрицательным. Только при этом условии результирующее реактивное сопротивление равнонулю, а вот активное, омическое, вполне вещественная величина. В таком случае - откуда в ЛМ может появиться отрицательное сопротивление? В учебнике по радиотехнике сказано, что отрицательное сопротивление (ОС) появляется только при наличии в устройстве цепи обратной связи. Благодаря этому часть выходного сигнала с выхода устройства попадает на его вход. Обратная связь бывает положительной и отрицательной. Если фазовая характеристика устройства обратной связи такова, что сигнал, пришедший через цепь обратной связи, совпадает по фазе с выходным сигналом, то любое приращение выходного сигнала приведет к увеличению сигнала на выходе. Такая обратная связь называется положительной. При сдвиге фаз на 180° схемавозбудится и в ней могут возникнуть периодические колебания. При наличии отрицательной обратной связи все происходит наоборот.
|
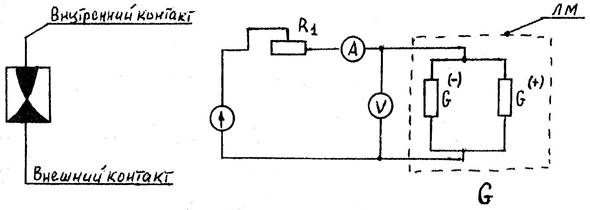
| Рис.6 |
Известно, что ОС обладают только те устройства, которые имеют положительную обратную связь по силе тока или напряжению. ЛМ представляет собой пространственный виток с весьма малым активным сопротивлением. Следовательно, основную роль в данном случае играет сила тока. Поэтому можем рассматривать ЛМ как устройство с отрицательной проводимостью. (Теория теорией, но эксперимент всегда был главным арбитром.)
Для окончательного решения вопроса о природе ОС в ЛМ необходимо снять вольтамперную характеристику. (ВАХ) его. Для этого требуется выполнить несколько условий. Первое условие состоит в том, что источник тока должен иметь внутреннее сопротивление меньшее, чем у ЛМ (менее 10-3 Ом), Условия согласования сопротивления ЛМ с внутренним сопротивлением источника тока могут быть выполнены и чисто конструктивным путем. Так, варьируя толщину и ширину проводника ЛМ, можно изменять внутренние сопротивления ЛМ и источника тока в некоторых пределах. Если первое условие не выполнить, то получим ВАХ только источника тока, а не ЛМ.
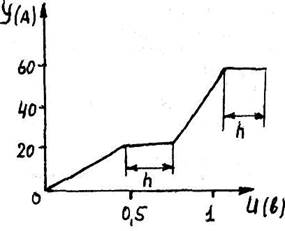
Второе условие заключается в том, что при подключении к прибору с ОС последовательно или параллельно активного сопротивления R ВАХ системы "прибор с ОС плюс сопротивление R" станет заметно отличаться от ВАХ самого прибора. Отметим, что сопротивление R может состоять из сопротивления проводов, подводящих ток. Во всех случаях сопротивление проводов должно быть намного ниже сопротивления ЛМ, а, следовательно, сечение их — быть наибольшим. Соберем схему (рис.6), в которой сопротивление R складывается из сопротивления амперметра, переменного сопротивления R1 и сопротивления подводящих ток проводов. Изменяя величину сопротивления R1, можно измерять значения силы тока и напряжения "по точкам". [Более точную схему генератора тока с выводом ВАХ на экран осциллографа можно найти в книге А. Бароне, Дж. Патерно, Эффект Джозефсона (физика и применения), пер, с англ. М, "Мир", 1984, с.84-87]. Пользуясь схемой рис.6 получили ВАХ ЛМ с алюминиевым проводником (рис.7А)
А
| Рис.7 | 
Б
|
На рис.7Б изображена классическая ВАХ прибора с отрицательной проводимостью (h — участок отрицательной проводимости на обоих рисунках). Для выяснения ситуации, является ли ЛМ устройством с ОС или устройством с отрицательной проводимостью, необходимо подключить дополнительный элемент (сопротивление) в цепь прибора последовательно или параллельно и снять ВАХ. Как видно из ВАХ ЛМ (рис.7А), на участках h сила тока стабильна, а напряжение увеличивается. Из радиотехники известно, что подобная характеристика получается при включении туннельного диода и параллельного ему сопротивления (рис.8). При незначительном сопротивлении R характеристика будет похожа на изображенную на рис.7А. Рассмотрим ВАХ ЛМ с закороткой в точке винтового перехода (рис.9А). А этом случае имеем сложную ВАХ (рис.9Б), которую можно интерпретировать как сочетание ВАХ нескольких полупроводниковых приборов: тиристора, туннельного диода, варистора.
| Рис.8 |
1 - кривая ВАХ туннельного диода;
2 - кривая ВАХ туннельного диода с параллельным сопротивлением (включение показано справа)
Из вышесказанного следует, что ЛМ из-за поверхностных явлений в полупроводниковых слоях в месте их контакта является весьма сложным устройством и при определенных условиях может быть источником мощных СВЧ-колебаний.
А
| 
Б
|
Рис.9
Таким образом, при работе ЛМ в качестве устройства с ОС необходимо соблюдение трех условий;
1) внутреннее сопротивление источника тока должно быть меньше или равно сопротивлению ЛМ ( ≤ 10-3 Ом);
2) тщательность изготовления ЛМ;
3) обязательное снятие перед каждым экспериментом ВАХ ЛМ плюс подводящих ток проводов, выключателей, предохранителей и т.д., в целях появления ОС.
Необходимым и достаточным условием появления ОС на ВАХ любого прибора является наличие положительной обратной связи по силе тока или напряжению, охватывающей не менее двух источников изменения проводимости (СА. Гаряинов, И.Д. Абезгауз. Полупроводниковые приборы с отрицательным сопротивлением, М., "Энергия", 1970, с.7-46), Один источник найден, приступим к поиску второго. Поскольку появление черных шаровых молний и прочих "чудес" только генерацией, мощных СВЧ-колебаний не объяснишь, приступим к рассмотрению топологических особенностей листа Мёбиуса (ЛМ), а затем и бутылки Клейна, так как именно с этой фигурой в дальнейшем в основном будем иметь дело.
Часть 2
Итак, продолжим поиск и представим себе, что все геометрические тела можно разделить на ориентируемые и на не ориентируемые. Но что же понимать под ориентацией? Предположим, что у нас есть три выделенных пункта (выделенных — значит, обособленных) А, В, С (рис.10), Все они соединяются дорогами с односторонним движением так, как показано на рис.10А. Введем ограничение. По дороге СВ можно ехать только в направлении, показанном стрелкой (рис.10Б). Такое незначительное ограничение полностью разрушает цикл и пункты А, В, С становятся обособленными и не связанными один с другим, т.е. неориентированными. Однако из каждого положения есть выход. Обратимся к рис. 10В. Из пункта А направляемся к пункту В, а из него удаляемся в ∞, возвращаемся из ∞ в пункт С и обычным путем попадаем в пункт А. Таким образом, определяем первое условие: ориентированные системы являются системами замкнутыми и в силу этого могут существовать только в пространствах целочисленных значений больше 1, 2, 3, 4, 5, …, n. Неориентированные системы являются системами вроде бы незамкнутыми, поскольку в своем составе имеют одну или несколько бесконечно удаленных точек, В геометрии такие точки называются СОБСТВЕННЫМИ. Неориентированные системы неустойчивы, они как бы промежуточномерны. (К примеру, размерность 1,5 или 3,7 — ни то, ни се). В дальнейшем мы докажем, что неориентированные системы являются тем средством, которое позволяет физически проникнуть в пространства иных размерностей, но не одномерного.
| ||
| А | Б рис.10 | С |
Как можно себе это представить? Возьмем полоску бумаги АВСД (рис11А). Один конец ее повернем перпендикулярно первому так, как показано на рис.11Б. Получим трехмерную винтовую фигуру, скрутку. Это очень интересное представление позволяет физически "пощупать" бесконечность и наглядно понять те особенности, которые выявятся при переходе через нее. Спроектируем фигуру на какую-нибудь поверхность и получим проекцию — тень (рис.11С). Из полученного построения можно сделать следующие выводы. Во-первых, поворот, перпендикулярный исходному, еще не означает "выхода" в пространство высшего измерения. Только ВСЯ полоска, наблюдаемая к тому же из пространства высшего измерения, представляется частью этого пространства. Во-вторых, поворот в пространстве, перпендикулярном пространству с исходным измерением, есть достижение бесконечно удаленной точки этого пространства и переход через нее. В-третьих, объект, который переходит в пространство высшей размерности, теряет одно измерение для наблюдателя, находящегося в пространстве исходного измерения. На рис.11 видно, что прямая ДС при повороте на 90° и проецировании на поверхность образовала точку, условно обозначенную СД. Отсюда следует четвертый вывод: тело, попадая в пространство высшей размерности, как бы увеличивает свою плотность для наблюдателя, находящегося в исходной размерности (точки С, Д превращаются в одну точку СД). К тому же параллельные линии пересекаются в бесконечно удаленной точке. Значит, здесь мы не вправе пользоваться обычной евклидовой геометрией, а имеем полное право использовать геометрию Лобачевского. Конечно, достижение бесконечности в геометрии вещь обычная (вспомним хотя бы стереографическую проекцию). Однако пример, представленный на рис.11, более нагляден.
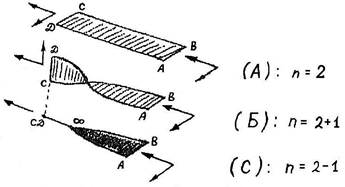рис.11
| 
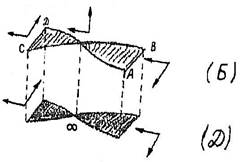рис.12
|
А что же там дальше,… за бесконечностью? "Довернем" край полоски и получим фигуру, изображенную на рис.12Б. Она имеет интересное свойство. Предположим, что вектор, стрелка АВ, пройдя через точку скрутки, через винтовой переход меняет направление и исчезает в точке ∞. Вектор движения вдоль полоски при этом сохраняется. Спроектируем фигуру (см. рис.12Б) на поверхность и получим тень исходного измерения, в данном случае двухмерного (рис.12Д). Не правда ли, картина похожа на геометрический ход лучей в оптической линзе? Делаем вывод: материя, пройдя пространство с размерностью n + 1 (в нашем случае n = 3), меняет знак или, как говорят, претерпевает инверсию, т.е. становится отрицательной. Соединив точку А с точкой С и точку В с точкой Д, получим лист Мебиуса - односторонний цилиндр, который приобретает свои особенные свойства. К разбору последнего мы сейчас и перейдем.
В геометрии принято изучать свойства фигур, образующихся при пересечениях более простых. Так, куб образуется при пересечении двух бесконечно протяженных параллелепипедов или в общем, топологическом случае - двух цилиндров, поскольку цилиндр без разрывов может быть деформирован в сечении и стать квадратным.
На нескольких примерах рассмотрим, как при пересечении трех гиперцилиндров получается лист Мебиуса и какие полезные выводы следуют из такого построения. На рис.13А изображено объемное метрическое представление бесконечного цилиндра. Предполагается, что прямой для нас цилиндр на самом деле есть тороид бесконечно большого радиуса. Если смотреть из некоторой точки очень длинной трубы, например нефтепровода, то в перспективе сечение трубопровода уменьшается и на горизонте превращается в точку, называемую бесконечно удаленной (рис.13Б). Если каким-либо образом мы попадем в четырехмерное пространство, то увидим, что цилиндр, пройдя бесконечно удаленную точку, снова начинает приобретать метрические свойства, только он будет состоять из отрицательной материи и внутренняя часть его окажется снаружи, а наружная — внутри (рис.13С). Дополним уже сделанное еще одним построением (рис.14). Приведем в соответствие положительное и отрицательное пространства. Соединим оба типа пространств, причем процесс соединения происходит вне этих пространств, т.е. фигура, представленная на рис.14, на самом деле четырехмерная.
Метрическое трехмерное пространство, бесконечность не определена
| рис.13 |
Гиперцилиндр. Неполное трехмерное проектное пространство. Несобственная бесконечно удаленная точка
| 
Полное четырехмерное проектное пространство. Собственная бесконечно удаленная точка
|
| Соответствие между положительным и положительным пространствами рис.14 |
В сечении трех гиперцилиндров с осями X, Y, Z имеем три бесконечно удаленные точки. В сечении цилиндров образуется лист Мебиуса (заштрихован). Построение, изображенное на рис.15, родилось при анализе условий образования шаровой молнии с уступами (ШМ, напоминающая голову с ушами. См. фотографию на обложке № 15 настоящего вестника). Таким образом, и шаровые молнии, и светящиеся колпаки, и галактики есть отображение исходной неориентированной фигуры в трех- или четырехмерном пространстве. Имеется в виду наше трехмерное пространство плюс бесконечно удаленная пространственная точка. Поскольку мы начали свободно оперировать понятием "бесконечно удаленная собственная точка", нелишне заметить, что такое понятие невозможно в нашем обычном метрическом пространстве, но оно уже имеет место в пространстве проективном (Любознательный читатель может познакомиться с геометрией проективного пространства в книге Д. Гильберта и С. Кон-Фоссена "Наглядная геометрия", М, "Наука", 1981, с.126; 297; 338-340). Исходя из принципов организации проективного пространства, находим, что в таком пространстве отсутствуют замкнутые объемы. Из полностью герметичного объема можно спокойно выйти и попасть во внешнее пространство, не прорезая в нем отверстий и не проламывая стен. Что же для этого нужно? Нужно в герметичном объеме создать условия для возникновения проективного пространства (при этом совершенно безразлично, какого типа полями для этого воспользуемся), достичь бесконечно удаленной точки, вернуться обратно и попасть в любое место, какое захочется. Действительность, однако, не так прекрасна и проста, как кажется. При движении к бесконечно удаленной точке необходимо развить предельно возможную скорость для нашего пространства. Мы знаем, что она равна скорости света. А так как есть ограничение, которое гласит, что для достижения скорости света частицей, обладающей массой, нужна бесконечная энергия, то на каком-то этапе приближения к бесконечности мы неизбежно превратимся в сгусток лептонов.
Предположим, что мы не сделаем глупости и не станем "отражаться" назад, ибо в этом случае последствия непредсказуемы, в лучшем случае мы размажемся по всей нашей Вселенной, Представим, что мы летим вперед за бесконечность. Через некоторое время мы влетаем в отрицательное пространство и, постепенно удаляясь от бесконечности, начинаем обретать плоть и попадаем в абсолютно необычный для нас мир. Солнце там черное и свет, идущий от него, тоже черный. А вот небо сияет и на нем рассыпаны черные точки звезд, туманностей, галактик. Черный свет не нагревает, а охлаждает, не отталкивает, а притягивает. И энергетика у местных жителей должна быть другой. Чтобы осуществить обратный переход, а это совсем не просто, мы по внепространственной дуге (см. рис.14) попадаем в наше положительное пространство. Но поскольку мы теперь состоим из отрицательной материи (не путать с антивеществом, так как вещество и антивещество различаются только зарядами), нам придется опять пройти через бесконечно удаленную точку и попасть в отрицательный мир, состоя уже из положительной материи. Опять осуществляем внепространственный переход, но уже в своем удобном и родном обличие и привычном мире. Какое счастье! Путешествие закончено. Конечно, ситуация эта придумана. На самом деле, никто никуда не движется и бесконечно удаленная точка представляет собой просто область пространства, в котором обычные физические законы не работают.
| Рис. 15 |
При "движении" к бесконечности постепенно убеждаемся, что привычные физические представления изменяются, иногда до неузнаваемости (Все происходит так, как описано в №14 настоящего вестника, июль 1995 г. Тогда мы смогли вовремя остановиться). Вероятно, расплывание предметов есть переход вещества в более разряженное состояние, что свидетельствует о движении к точке перехода, т.е. бесконечности. Препятствием пермеации (от лат. permeo — проницаю), т.е. прохождению одного тела сквозь другое, служит внутрикристаллическое электрическое поле. Налицо два варианта пермеации. Первый — нейтрализация электрического поля в месте проникновения и проход тела во внутреннюю полость или выход из нее без взаимодействия (возможное объяснение хирургических операций филиппинских целителей). Второй — нейтрализация внутрикристаллического электрического поля в проникающем теле (возможный сценарий для привидений, фантомов). Тут самое время вспомнить о положительной обратной связи — внепространственной дороге, соединяющей положительный мир с отрицательным, есть и вторая причина возникновения положительной обратной связи. В чем она выражается? Выражается она в информации, накопленной в обоих мирах в разных состояниях.
Вернемся к ЛМ и рассмотрим еще одно его свойство. Для этого выберем фиксированную точку на ЛМ и совершим обход вдоль его поверхности до того момента, когда точка старта и точка финиша станут соосны. При этом опишем впространстве некоторую незамкнутую кривую h1. Двигаясь далее в том же направлении, придем к начальной точке. Путь, пройденный во втором случае, обозначим через h2. Можно утверждать и это легко доказывается, что h1 = h2. Поскольку ЛМ есть односторонний цилиндр, а любое тело в нашем трехмерном пространстве имеет толщину, то за счет третьего измерения существует разность длин путей внутренней и наружной поверхностей объемов (при условии, что они геометрически правильны). У ЛМ эта разность равна нулю и ЛМ при любой толщине диэлектрика должен иметь такую конфигурацию электрического и магнитного полей, как будто толщины нет вовсе, а ЛМ сделан из одного куска металла. Чем не нуль-переход! Сигнал, посылаемый из внутренней точки ЛМ вдоль его поверхности, должен достичь наружной точки (и наоборот) практически мгновенно. Такой эксперимент был проведен и все подтвердилось (но об этом позже).
Раз ЛМ обладает такими удивительными свойствами, неплохо было бы понять, к какому классу поверхностей его отнести. Классический пример. ЛМ представляет собой односторонний цилиндр в параболической геометрии. В геометрии ЛМ есть односторонняя поверхность БЕЗ ТОЛЩИНЫ. Электрический аналог - свернутая в виде ЛМ полоска меди.
Рис. 16
| 
рис. 17
|
Но в параболической геометрии существует еще одна неориентированная фигура, которая может быть трехмерной. Это — неориентированный объем, односторонний тор или, что то же самое, бутылка Клейна (БК) (рис.16), Опуская многие замечательные свойства БК (см. Н.В. ЕФИМОВ "Высшая геометрия", М., 1961, с.568 - 580), рассмотрим интересующее нас. Разрезав БК вдоль замкнутой кривой (рис.17), получим два ЛМ, Какой вывод можно сделать из проведенного действия? Каждый из полученных ЛМ представляет собой проводник, а линия разреза может быть заполнена диэлектриком. Поэтому, когда мы изготовляем модели ЛМ даже из бумаги, в трехмерном пространстве мы получаем ВК, а не ЛМ. Модель будет еще нагляднее, если взять диэлектрик в виде квадратного бруска, с последующим скручиванием, изгибанием и склеиванием его. В этом случае на одной модели получаем два отдельных ЛМ. Рабочей же моделью остается БК в виде неориентированной полоски, у которой ширина намного больше толщины.
Какие же свойства БК для нас наиболее значительны в практическом смысле? Рассмотрим одну особенность БК. Винтообразным кривым на поверхности цилиндра соответствуют на БК замкнутые кривые, которые могут быть деформированы одна в другую и при различных значениях R (где R - число оборотов вокруг оси БК). Представим движущийся электрон в трехмерном пространстве. Магнитное поле его будет представлять собой спираль. Совсем другая картина вырисовывается при движении того же электрона по поверхности БК, Здесь магнитное поле образует сложную пространственную конфигурацию. Силовые линии поля взаимно переплетены, заузлены и образуют пространственную конструкцию с тугим узлом в центре (см. с.21 №16 вестника 1995 г.; последняя страница статьи Ивана Шахпаронова: «ТЕРМОЯД БЫЛ БЛИЗКОЙ И ДОСТИЖИМОЙ МЕЧТОЙ»). Сколько электронов, столько и петель. Заузленные петли магнитного поля образуют конструкцию с однонаправленным магнитным полем - магнитный монополь (Мон). Как и по теории, магнитный монополь может быть уничтожен только антимонополем, т.е., конструкцией со встречным магнитным полем. Согласно теории Мон, он будет обладать огромным электрическим зарядом, поэтому представленная конструкция одновременно демонстри