Численное решение.
Этот этап включает разработку алгоритмов для численного решения задачи, составления программ на ЭВМ и непосредственное проведение расчетов! Трудности этого этапа обусловлены, прежде всего, большой размерностью экономических задач, необходимостью обработки значительных массивов информации.
Анализ численных результатов и их применение.
На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних.
Взаимосвязи этапов
Возвратные связи этапов возникают вследствие того, что в процессе исследования обнаруживаются недостатки предшествующих этапов моделирования.
Уже на этапе построения модели может выясниться, что постановка задачи противоречива или приводит к слишком сложной математической модели. В соответствии с этим исходная постановка задачи корректируется. Далее математический анализ модели (этап 3) может показать, что небольшая модификация постановки задачи или ее формализации дает интересный аналитический результат.
Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает при подготовке исходной информации (этап 4). Может обнаружиться, что необходимая информация отсутствует или же затраты на ее подготовку слишком велики. Тогда приходится возвращаться к постановке задачи и ее формализации, изменяя их так, чтобы приспособиться к имеющейся информации.
Поскольку экономико-математические задачи могут быть сложны по своей структуре, иметь большую размерность, то часто случается, что известные алгоритмы и программы для ЭВМ не позволяют решить задачу в первоначальном виде. Если невозможно в короткий срок разработать новые алгоритмы и программы, исходную постановку задачи и модель упрощают: объединяют условия, уменьшают число факторов, нелинейные соотношения заменяют линейными, усиливают детерминизм модели и т.д.
Недостатки, которые не удается исправить на промежуточных этапах моделирования, устраняются в последующих циклах. Но результаты каждого цикла имеют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно быстро получить полезные результаты, а затем перейти к созданию более совершенной модели, дополняемой новыми условиями, включающей уточненные математические зависимости.
По мере развития и усложнения экономико-математического моделирования его отдельные этапы обособляются в специализированные области исследований, усиливаются различия между теоретико-аналитическими и прикладными моделями, происходит дифференциация моделей по уровням абстракции и идеализации.
4. Виды моделей:
По числу критериев эффективности экономико-математические модели делятся:
Ø Однокритериальные
Ø Многокритериальные
По учету неизвестных факторов экономико-математические модели делятся на:
Ø Детерминированные
Ø Стохастические
Ø Модели с элементами неопределенности
В детерминированных моделях неизвестные факторы не учитываются, а необходимая информация однозначна и достоверна. Детерминированные модели делятся на:
Ø Линейные модели. К ним относятся оптимизационные модели в которых целевая функция и ограничения линейны.
Ø Нелинейные модели. К ним относятся оптимизационные модели в которых либо целевая функция, либо ограничения, либо то или другое не линейны.
Ø Динамические модели. К ним относятся модели решение, которых моет быть представлено в виде многошагового, многоэтапного процесса, где вместо поиска оптимального решения для всей сложной задачи сначала находят оптимальные решения для нескольких более простых задач, аналогичного содержания.
Ø Графические модели. К ним относятся задачи в которых либо исходные данные, либо решение, либо то и другое заданы графически и т.д.
В стохастических моделях неизвестные факторы – случайные величины для которых известны функции распределения и различные стохастические характеристики:
Ø Математическое ожидание
Ø Дисперсия
Ø Среднее квадратическое отклонение
К ним относятся:
a. Модели стохастического программирования, которые содержат случайные величины, либо в целевой функции, либо в ограничениях.
b. Теории случайных процессов, которые предназначены для изучения процессов состояние которых в каждый момент времени является случайной величиной.
c. Модели теории массового обслуживания, которые изучает многоканальные системы занятые обслуживанием требований.
d. Теории полезности, которые изучают эффективность данного исследования.
Для моделирования ситуаций зависящих от факторов для которых нельзя собрать статистические данные значения которых неопределенны используются модели с элементами неопределенности. К ним относятся:
Ø Модели теории игр, где задача представляется в виде игры в которой участвует несколько игроков преследующие разные цели.
Ø Имитационные модели, в которых реальный процесс разворачиваются в машинном времени и прослеживаются результаты случайных воздействий на него.
5. Материальные модели основываются на чем то объективном существующем независимо от человеческого сознания (каких-либо телах или процессах). Материальные модели делят на физические (авто и авиамодели) и аналоговые основанные на процессах аналогичных в каком-то отношении изучаемом (процессы в электрических цепях и др.). Идеальные модели неразрывным образом связаны с человеческим мышлением, воображением, восприятием. Среди идеальных моделей можно выделить интуитивные модели, которые связаны с человеческим воображением; вербальные (текстовые) модели, которые используют последовательности предложений или символов некоторого языка для описания той или иной области действительности; математические модели- класс знаковых моделей широко использующих те или иные математические методы; информационные модели- класс знаковых моделей описывающих информационные процессы (возникновение, передачу, преобразование и использование информации) в системах самой разнообразной природы.
6. Математическая модель - это модель, созданная с помощью математических понятий.
По числу критериев эффективности экономико-математические модели делятся:
Ø Однокритериальные
Ø Многокритериальные
По учету неизвестных факторов экономико-математические модели делятся на:
Ø Детерминированные
Ø Стохастические
Ø Модели с элементами неопределенности
В детерминированных моделях неизвестные факторы не учитываются, а необходимая информация однозначна и достоверна. Детерминированные модели делятся на:
Ø Линейные модели. К ним относятся оптимизационные модели в которых целевая функция и ограничения линейны.
Ø Нелинейные модели. К ним относятся оптимизационные модели в которых либо целевая функция, либо ограничения, либо то или другое не линейны.
Ø Динамические модели. К ним относятся модели решение, которых моет быть представлено в виде многошагового, многоэтапного процесса, где вместо поиска оптимального решения для всей сложной задачи сначала находят оптимальные решения для нескольких более простых задач, аналогичного содержания.
Ø Графические модели. К ним относятся задачи в которых либо исходные данные, либо решение, либо то и другое заданы графически и т.д.
В стохастических моделях неизвестные факторы – случайные величины для которых известны функции распределения и различные стохастические характеристики:
Ø Математическое ожидание
Ø Дисперсия
Ø Среднее квадратическое отклонение
К ним относятся:
a. Модели стохастического программирования, которые содержат случайные величины, либо в целевой функции, либо в ограничениях.
b. Теории случайных процессов, которые предназначены для изучения процессов состояние которых в каждый момент времени является случайной величиной.
c. Модели теории массового обслуживания, которые изучает многоканальные системы занятые обслуживанием требований.
d. Теории полезности, которые изучают эффективность данного исследования.
Для моделирования ситуаций зависящих от факторов для которых нельзя собрать статистические данные значения которых неопределенны используются модели с элементами неопределенности. К ним относятся:
Ø Модели теории игр, где задача представляется в виде игры в которой участвует несколько игроков преследующие разные цели.
Ø Имитационные модели, в которых реальный процесс разворачиваются в машинном времени и прослеживаются результаты случайных воздействий на него.
7. Роль прикладных экономико-математических исследований.
Можно выделить, по крайней мере, четыре аспекта применения математических методов в решении практических проблем.
1. Совершенствование системы экономической информации. Математические методы позволяют упорядочить систему экономической информации, выявлять недостатки в имеющейся информации и вырабатывать требования для подготовки новой информации или ее корректировки. Разработка и применение экономико-математических моделей указывают пути совершенствования экономической информации, ориентированной на решение определенной системы задач планирования и управления. Прогресс в информационном обеспечении планирования и управления опирается на бурно развивающиеся технические и программные средства информатики.
2. Интенсификация и повышение точности экономических расчетов. Формализация экономических задач и применение ЭВМ многократно ускоряют типовые, массовые расчеты, повышают точность и сокращают трудоемкость, позволяют проводить многовариантные экономические обоснования сложных мероприятий, недоступные при господстве "ручной" технологии.
3. Углубление количественного анализа экономических проблем. Благодаря применению метода моделирования значительно усиливаются возможности конкретного количественного анализа; изучение многих факторов, оказывающих влияние на экономические процессы, количественная оценка последствий изменения условий развития экономических объектов и т.п.
4. Решение принципиально новых экономических задач. Посредством математического моделирования удается решать такие экономические задачи, которые иными средствами решить практически невозможно, например: нахождение оптимального варианта народнохозяйственного плана, имитация народнохозяйственных мероприятий, автоматизация контроля за функционированием сложных экономических объектов.
Сфера практического применения метода моделирования ограничивается возможностями и эффективностью формализации экономических проблем и ситуаций, а также состоянием информационного, математического, технического обеспечения используемых моделей. Стремление во что бы то ни стало применить математическую модель, может не дать хороших результатов из-за отсутствия хотя бы некоторых необходимых условий.
В соответствии с современными научными представлениями системы разработки и принятия хозяйственных решений должны сочетать формальные и неформальные методы, взаимно усиливающие и взаимодополняющие друг друга. Формальные методы являются, прежде всего, средством научно обоснованной подготовки материала для действий человека в процессах управления. Это позволяет продуктивно использовать опыт и интуицию человека, его способности решать плохо формализуемые задачи.
8. В детерминированных моделях неизвестные факторы не учитываются, а необходимая информация однозначна и достоверна. Детерминированные модели делятся на:
Ø Линейные модели. К ним относятся оптимизационные модели в которых целевая функция и ограничения линейны.
Ø Нелинейные модели. К ним относятся оптимизационные модели в которых либо целевая функция, либо ограничения, либо то или другое не линейны.
Ø Динамические модели. К ним относятся модели решение, которых моет быть представлено в виде многошагового, многоэтапного процесса, где вместо поиска оптимального решения для всей сложной задачи сначала находят оптимальные решения для нескольких более простых задач, аналогичного содержания.
Ø Графические модели. К ним относятся задачи в которых либо исходные данные, либо решение, либо то и другое заданы графически и т.д.
9. В стохастических моделях неизвестные факторы – случайные величины для которых известны функции распределения и различные стохастические характеристики:
Ø Математическое ожидание
Ø Дисперсия
Ø Среднее квадратическое отклонение
К ним относятся:
a. Модели стохастического программирования, которые содержат случайные величины, либо в целевой функции, либо в ограничениях.
b. Теории случайных процессов, которые предназначены для изучения процессов состояние которых в каждый момент времени является случайной величиной.
c. Модели теории массового обслуживания, которые изучает многоканальные системы занятые обслуживанием требований.
d. Теории полезности, которые изучают эффективность данного исследования.
10. Модели с элементами неопределенности. Для моделирования ситуаций зависящих от факторов для которых нельзя собрать статистические данные значения которых неопределенны используются модели с элементами неопределенности. К ним относятся:
Ø Модели теории игр, где задача представляется в виде игры в которой участвует несколько игроков преследующие разные цели.
Ø Имитационные модели, в которых реальный процесс разворачиваются в машинном времени и прослеживаются результаты случайных воздействий на него.
11 Системный подход – методологическое направление в науке основная задача, которого состоит в разработке методов исследования и конструирования сложно организованных объектов или процессов. Системный подход представляет собой этап в развитии методов познания методов исследовательской и конструкторской деятельности способов описания и объяснения природы анализируемых или искусственно создаваемых объектов. К числу важнейших задач в системном подходе моделирования относится:
Ø Разработка средств представления исследуемых и конструируемых объектов как систем.
Ø Построение обобщенных моделей разных классов и специфических свойств систем.
Ø Исследование теории структуры систем и различных системных концепций и разработок.
В системном исследовании анализируемый рассматривается как определенное множество элементов взаимосвязь которых обуславливает целостные свойства этого множества, свойства объекта как целостной системы определяется не только суммированием свойств отдельных элементов сколько свойствами его структуры и интегрируемыми связями объекта.
12 Можно выделить следующие аспекты применения математических методов в решении практических проблем:
1. Совершенствование системы экономической информации. Математические методы позволяют упорядочить систему экономической информации, выявлять недостатки в имеющейся информации и вырабатывать требования для подготовки новой информации или ее корректировки.
2. Интенсификация и повышение точности экономических расчетов. Формализация экономических задач и применение ЭВМ многократно ускоряют типовые, массовые расчеты, повышают точность и сокращают трудоемкость, позволяют проводить многовариантные экономические обоснования сложных мероприятий, недоступные при преобладании "ручной" технологии.
3. Углубление количественного анализа экономических проблем. Благодаря применению метода моделирования значительно усиливаются возможности конкретного количественного анализа; изучение многих факторов, оказывающих влияние на экономические процессы, количественная оценка последствий изменения условий развития экономических объектов и т.п.
4. Решение принципиально новых экономических задач. Посредством математического моделирования удается решать такие экономические задачи, которые иными средствами решить практически невозможно, например: нахождение оптимального варианта бизнес- плана, автоматизация контроля за функционированием сложных экономических объектов.
13 Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных и называется математическим программированием.
Для решения конкретной экономической задачи нужно прежде всего сформулировать ее математически (заменить экономическую задачу математической моделью). Такая формулировка распадается на 2 этапа:
Ø Сначала представляется в виде некоторой зависимости от искомых величины преследуемая цель (доход от реализации произведенной продукции, затраты на выполнение определенного объема работ и т.д.). Полученное выражение называется целевой функцией, функцией цели или функционалом данной задачи и записывается обычно в виде:
Ø Затем формулируются условия которые должны быть положены на искомые величины. Они вытекают из наличия ресурсов их необходимых удовлетворяющих определенных потребностей из условий технологии и из других экономических и технических факторов. Обычно эти условия представляют собой некоторые неравенства или уравнения. Поэтому задача математически формулируется следующим образом:
Ø Найти такие значения неизвестных которые удовлетворяли бы системе ограничений и доставляли функционалу мах или min совокупность численных значений или решений неизвестных часто называется планом задачи. Любой план удовлетворяющий системе ограничений является допустимым. Поэтому допустимый план максимирующий (минимизирующий) целевую функцию называется оптимальным. Таким образом решение задачи заключается в отыскивании оптимального плана среди множества допустимых.
14 Общая задача линейной оптимизации состоит в нахождении максимума (минимума) линейной функции:
Функцию Z называют целевой функцией, критерием оптимальности или линейной формой. Любое ограничение вида < либо = преобразуется в равенство добавлением к его левой части дополнительной неотрицательной переменной. Неравенство вида > либо = преобразуется в равенство вычитанием из его левой части дополнительной неотрицательной переменной.
В задачах линейного программирования все переменные имеют линейную зависимость.
Процедура формулировки всех задач линейной оптимизации:
1. Определение переменной задачи, значение которой нужно получить в пределах сущ. ограничений.
2. Определение цели и ограничение на ресурсы.
3. Описание цели через переменные задачи.
4.Описание ограничений через переменные задачи.
15 Алгоритм графического решения задачи:
I.Преобразовать неравенства задачи в равенства и построить в системе координат прямые, соответствующие этим равенствам.
II.Указать полуплоскости, задаваемые каждым неравенством задачи.
III. Определить область допустимых решений - многоугольник решений - выпуклое множество точек пресечения полуплоскостей, соответствующих неравенствам задачи.
IV. Построить вектор С=(с1;с2) - градиент функции Z.
V. Простроить прямую Z = c1x1 + с2х2 = 0, проходящую через начало координат и перпендикулярно вектору С.
VI.Передвигать прямую c1x1 + с2х2 = 0
а)в направлении вектора С, для нахождения точек, в которых целевая функция имеет максимальное значение либо
б) в направлении противоположном вектору С, для нахождения точек, в которых целевая функция имеет минимальное значение, либо
в) установить неограниченность функции на множестве планов.
VII. Определить координаты точки экстремума функции и вычислить значение целевой функции в этой точке.
При графическом методе решения возможны следующие случаи:
■ Существует единственное решение;
■ Существует бесконечное множество решений задачи;
■ Целевая функция не ограничена;
" Область допустимых решений - единственная точка;
• Задача не имеет решений.
Если система неравенств совместна, область ее допустимых решений, есть множество точек, принадлежащих всем заданным полуплоскостям. Это множество точек является выпуклым и называется областью допустимых решений или многоугольником решений. (Для задачи с n >3 переменными - многогранником решений).
16 Геометрическая интерпретация задачи линейного программирования позволяет найти решение графическим способом. Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость с граничными прямыми 
.
17 Алгоритм графического решения задачи:
I. Преобразовать неравенства задачи в равенства и построить в системе координат прямые, соответствующие этим равенствам.
II. Указать полуплоскости, задаваемые каждым неравенством задачи.
III. Определить область допустимых решений - многоугольник решений - выпуклое множество точек пресечения полуплоскостей, соответствующих неравенствам задачи.
VI. Построить вектор С=(с1;с2) - градиент функции Z.
VII. Простроить прямую Z = c1x1 + с2х2 = 0, проходящую через начало
координат и перпендикулярно вектору С.
VI.Передвигать прямую c1x1 + с2х2 = 0
а) в направлении вектора С, для нахождения точек, в которых целевая функция имеет максимальное значение либо
б) в направлении противоположном вектору С, для нахождения точек, в которых целевая функция имеет минимальное значение, либо
в) установить неограниченность функции на множестве планов.
VII. Определить координаты точки экстремума функции и вычислить значение целевой функции в этой точке.
При графическом методе решения возможны следующие случаи:
■ Существует единственное решение;
■ Существует бесконечное множество решений задачи;
■ Целевая функция не ограничена;
"Область допустимых решений - единственная точка; Задача не имеет решений.
18 Алгоритм графического решения задачи:
I. Преобразовать неравенства задачи в равенства и построить в системе координат прямые, соответствующие этим равенствам.
II. Указать полуплоскости, задаваемые каждым неравенством задачи.
III. Определить область допустимых решений - многоугольник решений - выпуклое множество точек пресечения полуплоскостей, соответствующих неравенствам задачи.
VIII. Построить вектор С=(с1;с2) - градиент функции Z.
IX. Простроить прямую Z = c1x1 + с2х2 = 0, проходящую через начало
координат и перпендикулярно вектору С.
VI.Передвигать прямую c1x1 + с2х2 = 0
а) в направлении вектора С, для нахождения точек, в которых целевая функция имеет максимальное значение либо
б) в направлении противоположном вектору С, для нахождения точек, в которых целевая функция имеет минимальное значение, либо
в) установить неограниченность функции на множестве планов.
VII. Определить координаты точки экстремума функции и вычислить значение целевой функции в этой точке.
При графическом методе решения возможны следующие случаи:
■ Существует единственное решение;
■ Существует бесконечное множество решений задачи;
■ Целевая функция не ограничена;
"Область допустимых решений - единственная точка; Задача не имеет решений.
19 Опорное решение доставляющее оптимальное значение целевой функции называют оптимальным решением или оптимальным планом.
Теорема. Если разрешающий элемент выбирать по наименьшему симплексному отношению, то вместо свободного члена разрешающей строки в новой симплексной таблице будет всегда число положительное, а остальные элементы столбца свободных членов не меняют знака.
20 Алгоритм нахождения опорного решения:
Ø Просматриваем элементы столбца свободных членов. Если все они положительны, то опорное решение найдено и начинается этап нахождения оптимального решения.
Ø Если среди столбца свободных членов имеются отрицательные, то выбираем любой из них и просматривая элементы строки с выбранным отрицательным свободным членом, фиксируем в ней отрицательные элементы. Любой столбец с отрицательным элементом в рассматриваемой строке принимаем за разрешающий. Если же в строке с отрицательным свободным членом нет отрицательных элементов, то система ограничений несовместна. Задача не имеет решения.
Ø Разрешающую строку находим по наименьшему симплексному отношению.
Ø С выделенным разрешающим элементом находим на пересечении разрешающей строки и столбца, рассчитываем новую симплексную таблицу.
21 Решим задачу симплексным методом, или методом последовательного улучшения плана. Этот метод является универсальным и применим при любом числе переменных. Процедура решения задачи основана на выборе некоторого исходного варианта плана и приведения его к оптимальному путем ряда последовательных преобразований. Для этого одни переменные вводятся в план, а другие исключаются из него. При этом значения переменных, входящих в план, рассчитываются так, что с каждым шагом план приближается к оптимальному и в конечном счете приходит к нему.
Вначале все функциональные ограничения преобразуем из неравенств в уравнения введением вспомогательных переменных:
Вспомогательные переменные имеют определенный экономический смысл: они обозначают неиспользованные производственные мощности в соответствующих цехах при выбранных значениях x1 и X2.
Представленные выше уравнениями ограничения могут быть записаны в векторной форме.
B целевой функции коэффициенты при вспомогательных переменных равны нулю, так как неиспользуемые мощности не приносят прибыли.
22 Алгоритм нахождения оптимального решения:
Ø Считаем, что в симплексной таблице найдено опорное решение. Просматриваем коэффициенты строки функции таблицы. Если все они неотрицательные, то оптимальное решение достигнуто. В этом решении все не базисные неизвестные =0, а базисные – свободным членам таблицы.
Ø Если среди коэффициентов строки функции имеются отрицательные, то выбираем среди них наибольший по абсолютной величине и столбец в котором находится этот коэффициент, берем за разрешающий
Ø Разрешающую строку находим по наименьшему симплексному отношению
Ø С найденным разрешающим элементом рассчитываем новую таблицу по следующим правилам:
Ø Разрешающий элемент заменяем обратно.
Ø Все элементы разрешающей строки делим на разрешающее число.
Ø Все элементы разрешающего столбца делим на разрешающее число с противоположным знаком.
Ø Оставшиеся элементы вычисляем по правилу прямоугольника:
,где ark-разрешающий элемент.
23
(4)
(5)
(6)
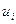произвольного знака при 
.
Задача (4)-(6), двойственная к задаче (1)-(3), строится по следующим правилам:
1) упорядочивается запись исходной задачи, т.е. если целевая функция задачи максимизируется, то ограничения неравенства должны быть вида 
, если минимизируется – то вида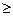 
. Выполнение этих условий достигается умножением соответствующих ограничений на (-1);
2) если исходная задача является задачей максимизации, то двойственная будет задачей минимизации. При этом вектор, образованный из коэффициентов при неизвестных целевой функции исходной задачи, совпадает с вектором констант в правых частях системы ограничений двойственной задачи, и, наоборот, коэффициентами при неизвестных целевой функции двойственной задачи являются соответствующие правые части системы ограничений исходной задачи;
3) каждой переменной 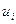двойственной задачи соответствует i-е ограничение исходной задачи, и, наоборот, каждой переменной 
прямой задачи соответствует j-е ограничение двойственной задачи;
4) матрица из коэффициентов при неизвестных двойственной задачи образуется транспонированием матрицы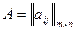 
, составленной из коэффициентов при неизвестных системы ограничений исходной задачи;
5) если на j-ю переменную исходной задачи наложено условие неотрицательности, то j-е ограничение двойственной задачи будет неравенством, в противном случае j-е ограничение будет равенством; аналогично связаны между собой ограничения исходной задачи и переменные двойственной.
24 Теорема 1. Если одна из двойственных задач имеет оптимальное решение 
, то и другая имеет оптимальное решение 
. При этом экспериментальные значения целевых функций задач совпадают, т.е.
.
Теорема 2. Если какая-то переменная 
оптимального решения исходной задачи положительна, j-е ограничение двойственной задачи ее оптимальным решением обращается в строгое равенство.
Если оптимальное решение исходной задачи обращает какое-то i-t ограничение в строгое неравенство, то в оптимальном решении двойственной задачи переменная 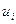равна нулю.
25 Алгоритм двойственного симплекс-метода сводится к следующему:
Этап 1
1. Просматривают коэффициенты f – строки; если все они неотрицательны, то переходят к пункту 1 этапа 2.
2. Если в f – строке имеется отрицательный коэффициент, то выделяют столбец, содержащий этот коэффициент.
3. В выделенном столбце отыскивают отрицательное число и содержащую его строку полагают разрешающей. Если в выделенном столбце нет отрицательных чисел, то задача не имеет решения.
4. Вычисляют двойственные отношения (отношения элементов f – строки к элементам разрешающей строки). Наименьшее из соотношений определяет разрешающий столбец.
5. С найденным разрешающим элементом делают шаг обыкновенных жордановых исключений. Анализ таблицы начинают с пункта 1.
Этап 2.
1. Просматривают столбец свободных членов; если все элементы столбца неотрицательны, то оптимальное решение достигнуто.
2. Если в столбце свободных членов есть отрицательные элементы, то среди них находят наименьший. Этот элемент определяет разрешающую строку.
3. Разрешающий элемент находят по наименьшему двойственному отношению. Если разрешающей строке нет положительных элементов, то задача не имеет решения.
4. С найденным разрешающим элементом делают один шаг обыкновенных жордановых исключений. Анализ полученной таблицы начинают с пункта 1 этапа 2.
26 Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления 
в п пунктов назначения 
. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
27 Транспортная задача с нарушенным балансом.
Для решения открытой транспортной задачи сведем ее к закрытой:
а) если 
, т.е. суммарный запас груза поставщиков больше суммарного спроса потребителей, то в задачу вводится фиктивный (п+1)-й потребитель с потребностью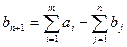 
и стоимостью перевозок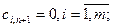 
б) если 
, то вводиться фиктивный (m+1)-й поставщик с запасом 
и стоимостью перевозок 
очевидно после добавления фиктивного потребителя или фиктивного поставщика транспортная задача будет закрытой, а следовательно, и разрешимой.
28 Методы построения опорного реш тр.задачи. Метод северо-западного угла.Метод min стоимости. (описать два метода). 29 Заполненных клеток в таблице для применения метода потенциалов должно быть m+n-1. Если это условие не выполняется, то в пустую клетку заносят 0 так чтобы не образовать замкнутый контур.Циклом или замкнутым контуром называется последовательность клеток ij таблицы транспортной задачи в котором каждые 2 рядом стоящие клетки находятся в одной строке или одном столбце при этом 1 и последней клетки совпадают.ТЕОРЕМА. Решение транспортной задачи будет оптимальным, если найдутся такие числа ui
и 
, называется соответствует потенциалами поставщиков и потребителей, которые будут удовлетворять условиям: 
30 Алгоритм метода потенциалов для транспортной задачи:
1. Находится первый опорный план.
2. Проверяется найденный опорный план на оптимальность, для чего:
2.1. Находятся потенциалы поставщиков 
и потребителей 
по формуле 
для 
Примечание. Так как в опорном плане заполнено m+n-1 клеток таблицы транспортной задачи, то для нахождения потенциалов по данному плану можно составить систему из m+n-1 линейно независимых уравнений с m+n неизвестными. Такая система называется неопределенной, и поэтому одной неизвестной (обычно 
) придают нулевое значение.
Проверяется выполнено ли условие 
для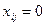 
или то же самое условие 
(для характеристик каждой свободной клетки). Если для всех свободных клеток таблицы выполнено условие то опорный план транспортной задачи является