ВЫСШАЯ МАТЕМАТИКА
Методические указания и контрольная работа №1
Для студентов Гродненского филиала кафедры «информационные системы и технологии»
МИДО БНТУ
специальность
«Экономика и управление на предприятии»
Решение типового варианта.
Задача 1. По координатам вершин  : А(4;4), В(-6;-1), С(-2;-4) найти:
: А(4;4), В(-6;-1), С(-2;-4) найти:
а) длину стороны АВ;
б) уравнение и длину высоты СD;
в) уравнение медианы АМ;
г) точку пересечения высоты СD и медианы АМ.
Решение.
Если  , то
, то
а)  .
.
б) Уравнение прямой АВ имеет вид: 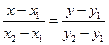 , т.е.
, т.е.  ,
,
 - уравнение прямой АВ. Тогда уравнение высоты СD можно записать как уравнение прямой, проходящей через точку С и перпендикулярной к прямой АВ, имеющей нормальный вектор
- уравнение прямой АВ. Тогда уравнение высоты СD можно записать как уравнение прямой, проходящей через точку С и перпендикулярной к прямой АВ, имеющей нормальный вектор  , который для этой прямой будет направляющим
, который для этой прямой будет направляющим  . Поэтому СD:
. Поэтому СD:  ,
,
 ,
,  - уравнение высоты СD.
- уравнение высоты СD.
Найдем точку D как точку пересечения прямых СD и АВ: 
 D(-4;0).
D(-4;0).
в) Поскольку медиана делит сторону ВС пополам, то из формул середины отрезка  , находим координаты точки М(-4;-2,5), где
, находим координаты точки М(-4;-2,5), где  .
.
Уравнение прямой АМ примет вид:  , т.е.
, т.е. 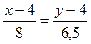 ,
,  , или
, или  - уравнение медианы АМ.
- уравнение медианы АМ.
г) Точку пересечения высоты CD и медианы АМ находим, решая систему

Значит, точка пересечения О  .
.
Задача 2. Даны координаты вершин пирамидыABCS: А(4;2;5), В(0;7;2), С(0;2;7), S(1;5;0).
Найти:
а) уравнение плоскости АВС;
б) уравнение прямой АВ;
в) уравнение прямой SN, перпендикулярной к плоскости АВС;
г) косинус угла между плоскостями АВС и ВСS;
д) объем пирамиды АВСS;
е) уравнение прямой SD параллельной прямой АВ;
ж) площадь грани АВС.
Решение.
а) Уравнение плоскости, проходящей через 3 точки 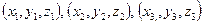 имеет вид:
имеет вид:
 , в нашем случае
, в нашем случае  .
.
Отсюда находим  ,
,  или
или  .
.
б) Уравнение прямой АВ, как прямой, проходящей через две точки  и
и  , примет вид:
, примет вид:
 , а в нашем случае
, а в нашем случае  .
.
в) Уравнение высоты SN, опущенной из вершины S на плоскость АВС можно записать как уравнение прямой, проходящей через точку S и перпендикулярной плоскости АВС, имеющей нормальный вектор  , который для этой прямой будет направляющим
, который для этой прямой будет направляющим
 - искомое уравнение высоты SN.
- искомое уравнение высоты SN.
г) Найдем уравнение плоскости ВСS:

 , т.е.
, т.е.  ,
,
следовательно 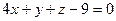 - уравнение плоскости ВСS.
- уравнение плоскости ВСS.
Косинус угла между плоскостями  и
и  найдем по формуле
найдем по формуле
 , отсюда
, отсюда
 ,
,  .
.
д) Объем пирамиды с вершинами  находится по формуле
находится по формуле 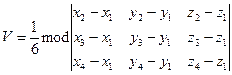 . В нашем случае
. В нашем случае

е) Т.к. прямая SD параллельна АВ, то направляющие векторы этих прямых совпадают  . Составим уравнение прямой SD, проходящий через точку S(1,5,0):
. Составим уравнение прямой SD, проходящий через точку S(1,5,0):

ж) Площадь грани ABC вычислим по формуле 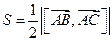 .
.
 ,
,
 .
.
Задача 3А. Вычислить определитель  .
.
Решение 1. Определитель третьего порядка вычисляется по формуле

Существует правило треугольника, облегчающее составление выражения, стоящего в правой части данной формулы:
Правило треугольника

по правилу треугольников получаем

Решение 2. Применим теорему Лапласа ко второй строке:  .
.
Задача 3Б. Вычислить определитель  .
.
Решение. Теорема Лапласа позволяет свести вычисление определителя n -го порядка к вычислению n определителей порядка n-1. Если в строке (столбце) имеются равные нулю элементы, то удобнее всего разлагать определитель по элементам той строки (столбца), которая содержит наибольшее число нулей.
Разложим определитель по третьему столбцу:

Задача 4А. М етодом Гаусса решить систему уравнений 
Решение. Запишем расширенную матрицу и методом Гаусса приведём её к трапецеидальному виду:
 ˜
˜  ˜
˜
Эквивалентная матрица получена сложением первой строки, умноженной на -3 последовательно со второй и третьей строками, умноженными на 2. Далее вторую строку складываем с третьей, умноженной на 11:
˜  .
.
Возвращаясь к системе уравнений получим, что соответствующая система будет иметь вид

Отсюда находим: 


Задача 4Б. М етодом Гаусса решить систему уравнений

Решение. Запишем расширенную матрицу системы:
 ˜
˜  ˜
˜
Эквивалентная матрица получена вычитанием из второй строки первой, умноженной на 3, из третьей – первой, умноженной на 5, из четвёртой – первой. Далее из второй строки последовательно вычитаем третью и четвёртую:
˜  ˜
˜  .
.
Исключив из матрицы третью нулевую строчку, получим, что соответствующая система будет иметь вид

В полученной системе число уравнений меньше числа неизвестных слагаемых, следовательно, система имеет бесконечное множество решений. Решая эту систему, начиная с последнего уравнения, получим: 
то есть 
Здесь  – базисные неизвестные,
– базисные неизвестные,  – свободная неизвестная. Так как
– свободная неизвестная. Так как  может принимать любые значения, то решение можем записать в виде
может принимать любые значения, то решение можем записать в виде 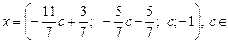 R.
R.
Задача 4В. М етодом Гаусса решить систему уравнений

Решение. Запишем расширенную матрицу системы:
 ˜
˜  ˜
˜  .
.
Здесь необходимо было сложить первую строку матрицы, умноженную на (-2) со второй, сложить первую строку матрицы, умноженную на (-4) с третьей и сложить первую строку матрицы, умноженную на (-5) с четвёртой. Затем в полученной матрице вторую строку, умноженную на (-1) прибавим к третьей. Данной матрице соответствует следующая система уравнений, равносильная исходной:

Третье уравнение этой системы не имеет смысла, поэтому система не имеет решений.
Задача 5А. Решить матричным методом систему 
Решение. Имеем  Найдем алгебраические дополнения
Найдем алгебраические дополнения
 ;
;  ;
;  ;
;
 ;
; 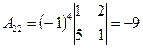 ;
;  ;
;
 ;
;  ;
;  .
.
Обратная матрица  . Находим
. Находим  :
:
 .
.
Таким образом 
Задача 5Б. Решить с помощью формул Крамера систему уравнений

Решение. Единственное решение квадратной системы с невырожденной матрицей можно получить по формулам Крамера:

где  – определитель матрицы системы, а
– определитель матрицы системы, а  ,
,  – определитель, полученный из определителя
– определитель, полученный из определителя  , заменой
, заменой  - го столбца столбцом свободных членов.
- го столбца столбцом свободных членов.
Выпишем матрицу системы  и столбец свободных членов
и столбец свободных членов  :
:
 ,
, 
Находим определитель системы:  Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:
Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

Итак, 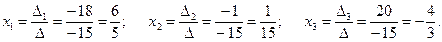
Ответ: 
Задача 6. Задача 5. Даны векторы  ,
,  и
и  .
.
Доказать, что векторы  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
Решение: Поскольку смешанное произведение
 ,
,
то векторы  образуют базис. Тогда вектор
образуют базис. Тогда вектор  можно представить в виде
можно представить в виде  . Это равенство равносильно следующим равенствам:
. Это равенство равносильно следующим равенствам:

поскольку равные векторы имеют равные координаты и координаты линейной комбинации векторов равны соответствующим линейным комбинациям одноименных координат.
Решив данную систему, находим

Итак, вектор  в данном базисе имеет координаты
в данном базисе имеет координаты  .
.
Задачи для контрольной работы №1.
Задача 1. Даны координаты вершин треугольника  . Найти:
. Найти:
а) длину стороны АВ;
б) уравнение и длину высоты СD;
в) уравнение медианы АМ;
г) точку пересечения высоты СD и медианы АМ.
| Вариант | А | В | С |
| (0;2) | (2;1) | (3;0) | |
| (1;2) | (3;4) | (-5;0) | |
| (-1;1) | (2;5) | (6;-2) | |
| (-1;3) | (0;2) | (4;-1) | |
| (3;4) | (-1;2) | (2;-1) | |
| (-1;1) | (1;5) | (3;-2) | |
| (1;1) | (3;0) | (-3;2) | |
| (-2;4) | (-6;8) | (6;-16) | |
| (-4;8) | (5;-3) | (10;6) | |
| (1;3) | (3;7) | (-1;1) | |
| (-2;0) | (2;-3) | (7;7) | |
| (2;1) | (5;-4) | (9;6) | |
| (1;1) | (8;1) | (6;8) | |
| (-4;-1) | (2;-5) | (5;3) | |
| (-1;-1) | (3;-4) | (7;6) | |
| (-2;1) | (2;3) | (-1;3) | |
| (-4;8) | (1;-2) | (6;9) | |
| (2;0) | (5;-3) | (10;5) | |
| (-4;7) | (0;-1) | (7;8) | |
| (-7;6) | (2;-6) | (7;4) | |
| (-5;7) | (4;-5) | (9;5) | |
| (-3;5) | (6;7) | (11;3) | |
| (-6;10) | (3;-2) | (8;8) | |
| (-3;8) | (4;-3) | (9;6) | |
| (-2;6) | (0;0) | (11;9) | |
| (-5;6) | (0;-5) | (3;10) | |
| (-1;0) | (5;-4) | (9;7) | |
| (-4;7) | (4;-2) | (8;9) | |
| (-6;0) | (5;-7) | (6;8) | |
| (-4;0) | (6;-3) | (7;6) | |
| (0;3) | (9;2) | (7;1) | |
| (-1;3) | (8;1) | (2;-4) | |
| (6;-2) | (2;5) | (-1;1) | |
| (6;5) | (1;-3) | (-8;9) | |
| (1;0) | (5;2) | (3;-1) | |
| (13;2) | (8;-8) | (-2;4) | |
| (10;5) | (7;-1) | (-2;11) | |
| (5;10) | (1;0) | (-9;12) | |
| (10;6) | (5;-3) | (-4;8) | |
| (5;-2) | (-1;2) | (0;3) |
Задача 2. Даны координаты вершин пирамиды ABCS. Найти:
а) уравнение плоскости АВС;
б) уравнение прямой АВ;
в) уравнение прямой SN, перпендикулярной к плоскости АВС;
г) косинус угла между плоскостями АВС и ВСS;
д) объем пирамиды АВСS;
е) уравнение прямой SD, параллельной прямой АВ;
ж) площадь грани АВС.
| Вариант | А | В | С | S |
| (3;4;5) | (1;2;1) | (-2;-3;6) | (3;-6;-3) | |
| (1;-3;4) | (0;-2;1) | (1;1;-1) | (5;6;7) | |
| (1;2;-1) | (-1;0;4) | (-2;-1;1) | (1;0;1) | |
| (1;2;3) | (4;-1;-2) | (4;0;3) | (4;3;6) | |
| (1;-1;-3) | (0;6;1) | (2;2;-2) | (0;-3;6) | |
| (1;1;4) | (2;-1;0) | (3;2;1) | (-1;4;3) | |
| (2;1;-3) | (1;1;0) | (-1;2;7) | (1;8;2) | |
| (-7;-5;6) | (-2;5;-3) | (3;-2;4) | (1;2;2) | |
| (2;1;3) | (0;0;2) | (1;1;1) | (6;9;3) | |
| (1;0;1) | (0;0;2) | (1;1;1) | (7;4;4) | |
| (2;3;1) | (4;-4;-2) | (1;0;0) | (4;7;5) | |
| (1;-2;-5) | (2;3;2) | (-1;0;5) | (-4;2;1) | |
| (1;3;1) | (-1;4;6) | (-2;-3;4) | (3;4;-4) | |
| (2;4;1) | (-3;-2;4) | (3;5;-2) | (4;2;-3) | |
| (1;3;4) | (0;1;2) | (2;5;0) | (1;-5;-7) | |
| (-5;-3;-4) | (1;4;6) | (3;2;-2) | (8;-2;4) | |
| (1;2;3) | (2;4;1) | (2;0;-3) | (-2;7;9) | |
| (1;-1;1) | (5;4;-2) | (-1;2;2) | (2;2;4) | |
| (3;-1;2) | (4;-1;-1) | (2;0;2) | (5;9;4) | |
| (7;1;4) | (9;-2;0) | (0;3;-3) | (0;1;2) | |
| (3;1;4) | (-3;-1;0) | (2;1;-3) | (7;3;2) | |
| (2;1;0) | (3;-1;-4) | (0;2;-2) | (8;0;2) | |
| (3;-1;-1) | (3;1;4) | (1;0;5) | (4;6;1) | |
| (2;1;-1) | (7;-1;3) | (0;3;3) | (5;2;1) | |
| (2;-3;7) | (-3;-1;5) | (9;0;1) | (-1;0;1) | |
| (7;-3;4) | (3;2;-1) | (4;1;1) | (5;-2;0) | |
| (1;1;0) | (2;1;-4) | (0;1;0) | (7;-1;-4) | |
| (1;-1;4) | (2;3;-4) | (1;0;-5) | (2;0;4) | |
| (2;-4;7) | (8;1;0) | (-1;-3;0) | (-1;0;-4) | |
| (1;-1;0) | (0;1;7) | (-1;-2;-3) | (4;3;1) | |
| (-1;0;4) | (-2;-1;1) | (1;0;1) | (1;2;-1) | |
| (0;-2;1) | (1;1;-1) | (5;6;7) | (1;-3;4) | |
| (2;4;2) | (-2;3;-5) | (4;3;-6) | (6;-5;3) | |
| (4;-1;-2) | (4;0;3) | (4;3;6) | (1;2;3) | |
| (0;6;1) | (2;2;-2) | (0;-3;6) | (1;-1;-3) | |
| (2;-1;0) | (3;2;1) | (-1;4;3) | (1;1;4) | |
| (1;1;0) | (-1;2;7) | (1;8;2) | (2;1;-3) | |
| (-4;6;3) | (3;-5;1) | (2;6;-4) | (2;4;-5) | |
| (0;0;2) | (1;1;1) | (6;9;3) | (2;1;3) | |
| (0;0;2) | (1;1;1) | (7;4;4) | (1;0;1) |
Задача 3. Вычислить определитель четвертого порядка:
1.  ; ;
| 2.  ; ;
| 3. 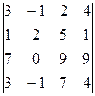 ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
| 7.  ; ;
| 8.  ; ;
|
9.  ; ;
| 10.  ; ;
| 11.  ; ;
| 12.  ; ;
|
13.  ; ;
| 14.  ; ;
| 15.  ; ;
| 16.  ; ;
|
17.  ; ;
| 18.  ; ;
| 19.  ; ;
| 20.  ; ;
|
21.  ; ;
| 22.  ; ;
| 23.  ; ;
| 24.  ; ;
|
25.  ; ;
| 26. 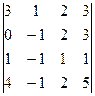 ; ;
| 27.  ; ;
| 28.  ; ;
|
29. 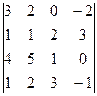 ; ;
| 30.  ; ;
| 31.  ; ;
| 32.  ; ;
|
33.  ; ;
| 34.  ; ;
| 35.  ; ;
| 36. 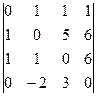 ; ;
|
37.  ; ;
| 38.  ; ;
| 39.  ; ;
| 40.  . .
|
Задача 4. Решить систему методом Гаусса (либо показать, что система несовместна).
.
1. 
| 2. 
|
3. 
| 4, 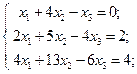
|
5. 
| 6. 
|
7. 
| 8. 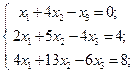
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
21. 
| 22. 
|
23. 
| 24. 
|
25. 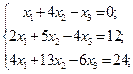
| 26. 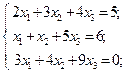
|
27. 
| 28. 
|
29. 
| 30. 
|
31. 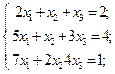
| 32. 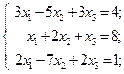
|
33. 
| 34. 
|
35. 
| 36. 
|
37. 
| 38. 
|
39. 
| 40. 
|
Задача 5. Решить систему методом Крамера и матричным методом.
1 1. 
| 1 2. 
|
1 3. 
| 1 4. 
|
5. 
| 1 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 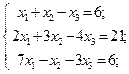
|
15. 
| 16. 
|
17. 
| 18. 
|
19. 
| 20. 
|
21. 
| 22. 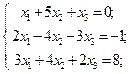
|
23. 
| 24. 
|
25. 
| 26. 
|
27. 
| 28. 
|
29. 
| 30. 
|
31. 
| 32. 
|
33. 
| 34. 
|
35. 
| 36. 
|
37. 
| 38. 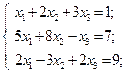
|
39. 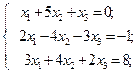
| 40. 
|
Задача 6. Даны векторы  . Доказать; что векторы
. Доказать; что векторы  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
| Вариант | 
| 
| 
| 
|
| (4;5;2) | (3;0;1) | (-1;4;2) | (5;7;8) | |
| (-1;2;0) | (-3;2;4) | (0;0;1) | (6;5;-4) | |
| (3;-5;2) | (4;5;1) | (-3;0;4) | (-4;5;-16) | |
| (1;-3;2) | (5;0;2) | (-2;4;1) | (8;1;3) | |
| (-2;3;5) | (1;-3;4) | (7;8;-1) | (1;20;1) | |
| (6;3;2) | (7;4;-5) | (4;2;2) | (4;1;2) | |
| (1;3;5) | (0;2;0) | (5;7;9) | (0;4;16) | |
| (3;0;4) | (6;3;4) | (1;2;3) | (-3;4;-2) | |
| (2;4;-6) | (1;3;5) | (0;-3;7) | (2;3;52) | |
| (2;5;6) | (1;2;2) | (1;0;1) | (3;2;2) | |
| (4;3;-1) | (5;0;4) | (2;1;2) | (0;12;-6) | |
| (-1;2;0) | (-3;2;4) | (0;0;1) | (4;3;-1) | |
| (3;4;-3) | (-5;5;0) | (2;1;-4) | (8;-16;17) | |
| (1;-3;2) | (5;0;2) | (-2;4;1) | (2;-1;-3) | |
| (-2;1;7) | (3;-3;8) | (5;4;-1) | (18;25;1) | |
| (6;3;2) | (7;4;-5) | (4;2;2) | (5;1;7) | |
| (1;0;5) | (3;2;7) | (5;0;9) | (-4;2;-12) | |
| (3;0;4) | (6;3;4) | (1;2;3) | (-1;5;-3) | |
| (2;1;0) | (4;3;-3) | (-6;5;7) | (34;5;-26) | |
| (2;5;6) | (1;2;2) | (1;0;1) | (4;3;2) | |
| (5;4;1) | (-3;5;2) | (2;1;-3) | (7;23;4) | |
| (-1;2;0) | (-3;2;4) | (0;0;1) | (6;3;-1) | |
| (2;-1;4) | (-3;0;-2) | (4;5;-3) | (0;11;-14) | |
| (1;-3;2) | (5;0;2) | (-2;4;1) | (6;-1;2) | |
| (-1;1;2) | (2;-3;-5) | (-6;3;-1) | (28;-19;-7) | |
| (6;3;2) | (7;4;-5) | (4;2;2) | (5;4;3) | |
| (1;3;4) | (-2;5;0) | (3;-2;-4) | (13;-5;-4) | |
| (3;0;4) | (6;3;4) | (1;2;3) | (3;-2;-2) | |
| (1;-1;0) | (-5;-3;1) | (2;-1;0) | (-15;-10;5) | |
| (2;5;6) | (1;2;2) | (1;0;1) | (4;2;0) | |
| (3;1;2) | (-7;-2;-4) | (-4;0;3) | (16;6;15) | |
| (-3;2;4) | (-1;2;0) | (0;0;1) | (6;5;-4) | |
| (-3;0;1) | (2;7;-3) | (-4;3;5) | (-16;33;13) | |
| (5;0;2) | (1;-3;2) | (-2;4;1) | (8;1;3) | |
| (5;1;2) | (-2;1;-3) | (4;-3;5) | (-45;15;-66) | |
| (7;4;-5) | (6;3;2) | (4;2;2) | (4;1;2) | |
| (0;2;-3) | (4;-3;-2) | (-5;-4;0) | (-19;-5;-4) | |
| (6;3;4) | (3;0;4) | (1;2;3) | (-3;4;-2) | |
| (3;-1;2) | (-2;3;1) | (4;-5;-3) | (-3;2;-3) | |
| (1;2;2) | (2;5;6) | (1;0;1) | (3;3;2) |