Задание 1. Составить структурную схему системы электросвязи и объяснить назначений ее отдельных элементов.
Структурная схема системы связи и назначение ее элементов
В данной работе рассматривается расчет основных характеристик системы передачи сообщений.
Каналом передачи называют совокупность технических средств и среды распространения, обеспечивающих передачу электрических сигналов с ограниченной мощностью и в ограниченной полосе частот (т.е. с ограниченной скоростью), электрическим сигналом (далее - сигнал) в общем смысле называется изменяющееся во времени и пространстве параметры электромагнитного поля. Под модуляцией понимается процесс изменения тех или иных параметров несущего сигнала под воздействием первичного сигнала. В случае если в качестве передаваемого сигнала используется синусоидально изменяющееся напряжение или ток, его параметрами можно считать амплитуду и полную фазу, содержащую в себе частоту и начальную фазу.

Аналитически сигналы есть функции времени и бывают дискретными и непрерывными (аналоговыми). Если сигнал как функция u(t) принимает только определенные дискретные значения u (например, 0 и 1), то он называется дискретным или, точнее, дискретным по состояниям. Если же сигнал может принимать любые значения в некотором интервале, то он называется аналоговым или непрерывным по состояниям. Под дискретным по времени сигналом необходимо понимать сигнал, заданный не на всей области значений времени, а только в определенные моменты tи. Рисунок 1.1 поясняет эти отличия. Здесь а – сигнал непрерывный по времени и по состояниям, б - дискретный по состояниям и по времени сигнал, в – непрерывный по состояниям и дискретный по времени сигнал, г – сигнал дискретный и по состояниям, и по времени.
Поскольку заранее известный (детерминированный) сигнал не может нести информации, то все сигналы, рассматриваемые в данной работе являются случайными процессами.
Длительностью сигнала Tc считается интервал времени, в пределах которого он существует, его динамическим диапазоном Dc – отношение наибольшей мгновенной мощности сигнала к той наименьшей мощности, которую необходимо отличать от нуля при заданном качестве передачи. За ширину спектра сигнала Fc принимается диапазон частот, в пределах которого сосредоточена основная его энергия. В технике связи спектр сигнала часто сознательно сокращают, т.к. аппаратура и линии связи имеют ограниченную полосу пропускаемых частот. Сокращение спектра осуществляется исходя из допустимых норм искажений сигнала. Так, например, в качестве частотного диапазона речевого сигнала в связи полагаем полосу от 300 Гц до 3.4 кГц.
Под термином сообщение понимается совокупность знаков (символов), содержащих ту или иную информацию, подлежащую передаче на расстояние
Рассмотрим далее структурную схему системы передачи сообщений и ее основные элементы (рисунок 1.2).
 |
Рис. 1.2. Структурная схема системы передачи сообщений
ИСТОЧНИК СООБЩЕНИЙ (ИС) – объект, которому необходимо передать некое сообщение в виде сигнала a(t).
ДИСКРЕТИЗАТОР (Д) – устройство, обеспечивающее дискретизацию сигнала a(t) по теореме Котельникова во времени.
КОДЕР (Код) – преобразователь дискретизированного во времени сигнала в кодированный.
МОДУЛЯТОР (Мод) – преобразователь сигналов кодовых импульсов в сигналы, пригодные для передачи по каналу связи.
КАНАЛ СВЯЗИ обеспечивает физический перенос сигнала на расстоянии по линии связи, внося в него при этом шумы и искажения.
ДЕМОДУЛЯТОР (Дем) – устройство, обеспечивающее обратное преобразование сигнала в удобном для передачи виде в дискретный по времени и состояниям сигнал.
ДЕКОДЕР (Дек) – преобразователь кодированного сигнала в дискретный по состояниям сигнал.
ФИЛЬТР-ВОССТАНОВИТЕЛЬ (ФВ) – фильтр нижних частот (далее ФНЧ), восстанавливающий переданный ИС сигнал из дискретизированного сигнала.
Линией связи называется среда, используемая для передачи сигналов от передатчика к приемнику. При передаче сигнал может искажаться и на него могут накладываться шумы n(t).
Для непрерывных каналов связи характерно: во-первых, линейность – тогда выходной сигнал является суперпозицией передаваемого сигнала и помехи, во-вторых, наличие помех на выходе канала, даже если на его вход не поступает сигнал, в-третьих, сигнал при передаче по каналу связи претерпевает задержку по времени и затухание по уровню. В реальных каналах всегда имеют место искажения сигнала, обусловленные несовершенством характеристик канала и, нередко, изменением параметров канала во времени.
Помехой называется любое случайное воздействие на сигнал, которое ухудшает верность воспроизведения передаваемых сообщений. В проводных каналах связи основным видом помех являются импульсные шумы и прерывания связи. Появление импульсных помех часто связано с автоматической коммутацией и перекрестными наводками. Прерывание связи есть явление в канале, когда передаваемый сигнал резко затухает или исчезает.
Практически в любом диапазоне частот имеют место внутренние шумы аппаратуры.
Шум бывает аддитивным (зашумленный сигнал есть арифметическая сумма полезного сигнала и шума, существующего во времени постоянно) и мультипликативным (то же, только наличие шума в канале в каждый момент времени определяется случайным процессом). Среди аддитивных шумов особое место занимает флуктуационная помеха, имеющая нормальное (гауссово) распределение.
Задание 2. Источник сообщений:
1. Записать аналитическое выражение и построить график одномерного закона распределения плотности вероятности Wa мгновенных значений случайного процесса a(t).
2. Найти математическое D процесса ожидание m1 и дисперсию a(t).
Источник выдает сообщение a(t), представляющее собой непрерывный стационарный процесс, мгновенные значения которого в интервале от amin до amax равновероятны, а основная доля мощности сосредоточена в полосе частот от 0 до FВ.
1. Для нахождения одномерной плотности вероятности мгновенных значений случайного процесса a(t) учтем, что все его мгновенные значения в заданном интервале равновероятны, и, следовательно, плотность вероятности будет постоянна в этом интервале и равна нулю вне этого интервала.
Значение плотности вероятности внутри интервала от amin до amax определим из условия нормировки:
 ;
;  ;
;  ;
;

Таким образом, аналитическое выражение для плотности распределения вероятности случайного процесса a(t) имеет вид:

|
| |||
 | |||
 | |||||||
 | |||||||
|
| ||||||
Рис. 2.1. Плотность вероятности случайного процесса a(t)
2. Найдем математическое ожидание M случайного процесса a(t):

Так как W(a) вне интервала от amin до amax равна 0, то получим:


 В
В
То есть получили, что среднее значение случайного процесса a(t)равно 5.1В.
Найдем дисперсию или математическое ожидание квадрата D случайного процесса a(t):


 ;
;  ;
;
 В
В
Задание 3. Дискретизатор
1. Определить шаг квантования по времени Δt.
2. Определить число уровней квантования L.
3. Рассчитать относительную мощность шума квантования, определив ее как отношение средней мощности шума квантования Ршк к средней мощности сигнала, т.е. дисперсии σ2.
4. Рассматривая дискретизатор как дискретный источник информации с объемом алфавита L, определить его энтропию Н и производительность Н'.
Передача информации от источника осуществляется по дискретной системе связи. Для этого сообщение a(t) в дискретизаторе квантуется по времени и по уровню с равномерным шагом. Шаг квантования по уровню Δa=0.1B.
1. Шаг квантования по времени  определяется из теоремы Котельникова:
определяется из теоремы Котельникова:

2. Число уровней квантования L при равномерном шаге  определяется как частное от деления размаха сигнала (amax-amin) на шаг квантования Δa.
определяется как частное от деления размаха сигнала (amax-amin) на шаг квантования Δa.

3. Для нахождения средней мощности шума квантования надо знать закон распределения шума – W(ξ). Так как мгновенные значения равновероятны в заданном интервале, то закон распределения шума W(ξ) в интервале aj-Δa/2≤ξ≤aj+Δa/2 будет равномерным и не будет зависеть от номера интервала.
Следовательно, средняя мощность шума квантования будет равна:

Закон определения шума определим из условия нормировки:
 ;
;  ;
;  .
.

Тогда средняя мощность шума квантования:


Относительная величина мощности шума квантования есть отношение Ршк к дисперсии случайного процесса a(t):

4. Энтропия – математическое ожидание количества информации или мера неопределенности сообщений.
Покажем, что при заданном законе распределения мгновенных значений процесса  все уровни квантования равновероятны. Для этого найдем вероятность j-го уровня квантования что равносильно вероятности попадания
все уровни квантования равновероятны. Для этого найдем вероятность j-го уровня квантования что равносильно вероятности попадания  в интервал
в интервал 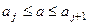 .
.
 ,
,
Т.е.  не зависит от j.
не зависит от j.
Тогда энтропия будет определяться как энтропия дискретного источника независимых сообщений, все символы которого равновероятны:
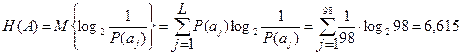 бит/сим.
бит/сим.
Производительностью такого источника будет суммарная энтропия сообщений, переданных за единицу времени:
 .
.
Задание 4. Кодер
1. Определить минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(ti).
2. Определить избыточность кода с одной проверкой на четность Рк.
3. Записать двоичную кодовую комбинацию, соответствующую передаче aj-го уровня, считая, что при примитивном кодировании на 1-м этапе aj-му уровню ставится в соответствие двоичная кодовая комбинация, представляющая собой запись числа в двоичной системе.
4. определить число двоичных символов, выдаваемых кодером в секунду Vk и длительность двоичного символа Т.
В кодере процесс кодирования осуществляется в два этапа. На 1-ом этапе производится безызбыточное (примитивное) кодирование каждого уровня квантованного сообщения a(ti) к-разрядным двоичным кодом. На 2-ом этапе к полученной к-разрядной двоичной кодовой комбинации добавляется один проверочный символ, формируемый простым суммированием по модулю 2 всех информационных символов. В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют нулевым символам кодовой комбинации, а отрицательные – единичным.
1. Найдем минимальное значение к, необходимое для кодирования всех L уровней квантованного сообщения a(ti).

2. Определим избыточность кода с одной проверкой на четность.

3. Представим число j=37 в двоичной системе счисления:

 |
Следовательно к-7 информационных символов кодовой комбинации будут иметь вид:
Определим проверочный символ в7 путем суммирования по модулю 2 всех к=7 информационных символов 
Учитывая, что правило суммирования по модулю 2 имеет вид:

 получим, что в8= 1.
получим, что в8= 1.
 |
Таким образом, искомая кодовая комбинация, соответствующая передаче а 37 уровня квантованного сообщения, будет иметь вид:
 4. Число двоичных символов, выдаваемых кодером в секунду Vк, определяется числом отсчетов (1/Δt) и числом двоичных символов n=к+1, приходящихся на один отсчет.
4. Число двоичных символов, выдаваемых кодером в секунду Vк, определяется числом отсчетов (1/Δt) и числом двоичных символов n=к+1, приходящихся на один отсчет.


Длительность двоичного символа определяется как величина, обратная Vk.


Задание 5. Модулятор
1. Определить параметры несущей. Изобразить временные диаграммы модулирующего в(t) и манипулированного s(t) сигналов, соответствующих передаче а j-го уровня сообщения а(t) /
2. Привести выражение и начертить график корреляционной функции модулирующего сигнала в(t) - Bв(τ).
3. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала в(t) - G в(f).
4. Определить условную ширину энергетического спектра модулирующего сигнала ΔF в (t) из условия ΔF в =αVk (где α выбирается от 1 до 3). Отложить полученное значение ΔF в на графике G в(f). Определить условную ширину энергетического спектра модулирующего сигнала методом равновеликого прямоугольника (с помощью СПМ). Выбрать оптимальное значение.
5. Записать аналитическое выражение модулированного сигнала s(t)=F[ в(t) ].
6. Привести выражение и построить график энергетического спектра модулированного сигнала Gs(f).
7. Определить условную ширину энергетического спектра модулированного сигнала ΔFs. Отложить полученное значение ΔFs на графике Gs(f).
В модуляторе синхронная двоичная случайная последовательность биполярных импульсов в(t) осуществляет манипуляцию гармонического переносчика U0cos(2πf0t).
Параметры несущей: U0=1B,
f0=100Vk=40 МГц.
Выражения сигналов:  ;
;
 .
.
1. Изобразим временную диаграмму модулирующего сигнала в(t).
 b(t)
b(t)
 |  |  | |||






 t
t













0 1 0 0 1 0 1 1
 S(t)
S(t)
 t
t
Рис.5.1. Временная диаграмма манипулированного сигнала s(t)
2. Для определения функции корреляции рассмотрим два сечения в моменты t1 и t2 (t2-t1=τ) и найдем математическое ожидание произведения X(t1)X(t1+τ).
Если τ>Т, то эти сечения принадлежат разным тактовым интервалам и произведение может с равной вероятностью принимать значения +1 и -1, так что его математическое ожидание равно 0.
Если τ<Т, то возможны два варианта: случай А, когда они принадлежат одному интервалу и, следовательно, X(t1)X(t1+τ)=1, и случай В, когда они принадлежат разным тактовым интервалам и X(t1)X(t1+τ) может с равной вероятностью равняться +1 и -1. Поэтому при τ<Т математическое ожидание X(t1)X(t1+τ) равно вероятности р(а) того, что оба сечения оказались в одном интервале. Случай А имеет место, если первое из двух сечений отстоит от начала тактового интервала не более чем Т-|τ|, а вероятность этого равна (Т-|τ|)/Т.
Тогда функция корреляции имеет вид:
 |


Рис. 5.3.
3. Найдем выражение для спектральной плотности мощности модулированного сигнала по теореме Винера-Хинчина:

 ;
; 
Так как В(τ) - функция четная, то

 ;
; 


Возьмем интеграл  по частям:
по частям:
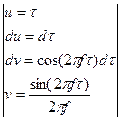

 |
Построим график спектральной плотности мощности модулирующего сигнала:
Рис. 5.2. График спектральной плотности мощности модулирующего сигнала
4. Найдем условную ширину спектра сигнала. Под условной шириной спектра сигнала понимают полосу частот, в которой сосредоточена основная доля мощности сигнала. Чем больше выбранное значение α, тем большая доля мощности будет сосредоточена в этой полосе частот.
Пусть α=2

Определим долю мощности, сосредоточенную п полосе частот от 0 до  .
.
 ;
; 


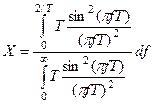
Рассмотрим по отдельности числитель и знаменатель этого выражения.

Возьмем этот интеграл по частям
U=sin2x; dU=sin2xdx;  ;
;  ;
;

 - интегральный синус;
- интегральный синус;  ;
;
Si(4π)=1.4922; Si(0)=0;  .
.
Аналогично получим,что  .
.
 ;
;  ;
;  .
.
То есть получили, что 95% всей мощности сигнала приходится на полосу частот от 0 до ΔF в.
5. Происходит модулирование сигнала  по правилу:
по правилу:

при  , тогда
, тогда 
при  , тогда
, тогда 
6. При ФМ выражение энергетического спектра модулированного сигнала имеет вид:


Тогда построим график энергетического спектра модулированного сигнала Gs(f).
 |
Рис.5.3.
7. Условная ширина энергетического спектра будет в 2 раза больше условной ширины энергетического спектра модулирующего сигнала.
 МГц
МГц
Задание 6. Канал связи
1. Определить мощность шума в полосе частот Fk=ΔFs
2. Найти отношение средней мощности сигнала к мощности шума.
3. Найти по формуле Шеннона пропускную способность канала в полосе Fk.
4. Определить эффективность использования пропускной способности канала Кс,.
Передача сигналов s(t) осуществляется по неискажающему каналу с постоянными параметрами и аддитивной флуктуационной помехой n(t) с равномерным энергетическим спектром G0 (белый шум).
Сигнал на выходе такого канала можно записать следующим образом:

Требуется:
1.
 |
График спектральной плотности мощности квазибелого шума имеет вид:
Рис. 6.1. …
Тогда мощность шума в полосе частот Fk равна:

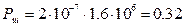 Вт
Вт
2. Для двоичных равновероятных символов s1(t) и s2(t) их средняя мощность будет равна:

где  и
и  - энергия сигналов;
- энергия сигналов; 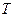 - длительность сигналов.
- длительность сигналов.
Энергия сигнала определяется как  .
.

 , (В2).
, (В2).
 Вт
Вт
Но так как мы используем не всю мощность ее сигнала, а только 95% всей мощности, то
 Вт – Мала! Если увеличить напряжение до 2 В, то получим:
Вт – Мала! Если увеличить напряжение до 2 В, то получим:
отношение средней мощности сигнала к мощности шума равно:
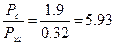
3. Пропускную способность канала связи найдем по теореме Шеннона:
 .
.
4. Найдем эффективность использования пропускной способности канала связи: 

Задание 7. Демодулятор
1. Записать правило решения демодулятора, оптимального по критерию максимального правдоподобия или неоптимального, или другого типа.
2. Записать алгоритм работы и нарисовать структурную схему демодулятора для заданного вида модуляции и способа приема.
3. Вычислить вероятность ошибки р оптимального демодулятора.
4. Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить вычисленное значение вероятности ошибки р.
В демодуляторе осуществляется оптимальная по критерию максимального правдоподобия некогерентная обработка принимаемого сигнала z(t)=s(t)+n(t).
1. Так как все символы передаются равновероятно, то правило максимального правдоподобия имеет вид:
Λi>Λj при i≠j
где  - отношение правдоподобия
- отношение правдоподобия
W(z| в i) - функция правдоподобия i-ой гипотезы
W(z|ш) - функция правдоподобия, что никакой сигнал не передавался
2. Для некогерентного приема при ДЧМ алгоритм работы оптимального по критерию максимального правдоподобия, может быть представлен в виде: