Лекция 8. Синтез КИХ-фильтров методом окон
1. Синтез идеального КИХ-фильтра.
2. Синтез КИХ-фильтра методом окон.
3. Итерационная процедура синтеза КИХ-фильтра методом окон.
Синтез идеального КИХ-фильтра
Постановка задачи: синтезировать идеальный КИХ-фильтр с ЛФЧХ.
Синтез ЦФ заключается в расчете _________________________________, которая для КИХ-фильтра имеет вид:
Следовательно, синтез КИХ-фильтра сводится к расчету _________________
Рассмотрим возможность синтеза идеального КИХ-фильтра на примере КИХ-фильтра типа 1 с идеальной АЧХ 
на рис. 8.1.
Рис. 8.1. АЧХ идеального ФНЧ
В основной полосе частот 
идеальная АЧХ равна:
(8.1)
где 
— частота разрыва (cutoff).
ЛФЧХ КИХ-фильтра типа 1 равна (табл. в Лекции 7):
. (8.2)
При известных АЧХ и ФЧХ запишем ЧХ идеального КИХ-фильтра:
. (8.3)
Периодичность ЧХ 
позволяет ее представить в виде __________________________________________
, (8.4)
с __________________________ 
— _____________________________________
. (8.5)
Синтез КИХ-фильтра сводится к _________________________
В точке 
имеем _________________________________. Раскроем/ Оопределим __________________________________________________________________
Окончательно (рис. 8.2, а):
(8.6)
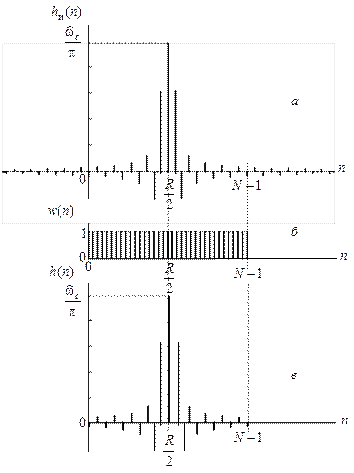
Рис. 8.2. ИХ идеального КИХ-фильтра (а), окно Дирихле (б), ИХ КИХ-фильтра (в)
Таким образом:
· ИХ 
идеального КИХ-фильтра, _______________________ относительно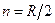 
, гарантируем _______________________ ФЧХ;
1. однако ______________________________ ИХ является ______________, не равной нулю _________________________ области времени, следовательно, нарушается условие ________________________________________: реакция _______________________________________________________________
Вывод: идеальный КИХ-фильтр __________________________________________
Синтез КИХ-фильтра методом окон
Идеальную ИХ используют для синтеза физически реализуемого КИХ-фильтра с ЛФЧХ методом окон. Суть данного метода заключается в _________________________________________________________________________
На рис. 8.2, б приведено прямоугольное окно 
, известное как окно____________
(8.7)
а на рис. 8.2, в — ИХ 
КИХ-фильтра в виде ____________________:
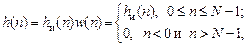(8.8)
что эквивалентно _______________ ряда Фурье (8.4), т. е. _____________________
Определим ЧХ _____________________ (8.8) — _____________ ЧХ ______________________ (8.3) и ЧХ ___________________ (8.7).
Определим ЧХ окна Дирихле — его____________________________
Проанализируем, к каким искажениям идеальной АЧХ приведет применение окна Дирихле.
Определим Фурье-изображение окна :
и оценим искажение идеальной ЧХ качественно.
ФЧХ окна __________________ с ФЧХ идеального КИХ-фильтра, следовательно, ФЧХ физически реализуемого КИХ-фильтра _________________________________
Искажения АЧХ физически реализуемого КИХ-фильтра иллюстрирует рис. 8.3, где приведена его амплитудная функция 
:
. (8.9)
и пунктиром отмечена АЧХ идеального КИХ-фильтра.
Рис. 8.3. Амплитудная функция КИХ-фильтра ФНЧ с окном Дирихле
Суть искажений вследствие применения окна Дирихле: вместо идеальной АЧХ с _______________ на частоте получаем ________________ функцию со следующими характерными признаками:
· на частоте разрыва всегда:
;
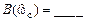· вместо разрыва получили ________________________, симметричную относительно ;
С ростом порядка КИХ-фильтра ее ширина ___________________, и в пределе при бесконечном порядке теоретически стремится ____________;
· вместо 1 в ПП и 0 в ПЗ получаем ________________ с максимальной амплитудой на границах _______________________
С ростом порядка КИХ-фильтра пульсации становятся _________________________, а их максимум ____________________________________
_________________________________ эффект Гиббса.
Для устранения эффекта Гиббса ____________________________________________ с максимумом в центре и монотонным спаданием к краям (рис. 8.4).
Рис. 8.4. Пример окна (не Дирихле)
"Платой" за устранение эффекта Гиббса является _______________________________
Поэтому при заданных граничных частотах ПП и ПЗ приходится _________________
С этим связан недостаток метода окон — невозможно синтезировать __________________________________________________________________________________________________________________________________________________
Достоинство метода окон заключается в __________________________, что позволяет использовать метод для синтеза КИХ-фильтров ________________________________
Итерационная процедура синтеза КИХ-фильтра методом окон
1. ______________________________________
2. Выбор окна и оценка порядка КИХ-фильтра.
3. Синтез КИХ-фильтра — расчет________________________________, который для КИХ-фильтра сводится к расчету ________________________________
Для синтеза КИХ-фильтров можно использовать только тип 1 или 2 (см. тип избирательности в табл. Лекции 7).
4. Уточнение порядка КИХ-фильтра.
Производится по результатам проверки выполнения требований к АЧХ (отклонения от 1 в ПП и 0 в ПЗ):
o не выполняются — порядок ______________________;
o выполняются — порядок _______________.
В итоге находят ________________________порядок 
, при котором выполняются требования к АЧХ.
ВНИМАНИЕ, При выборе окна Кайзера автоматически синтезируется КИХ-фильтр минимального порядка!
5. Выбор структуры КИХ-фильтра — ________________________________