Функция полезности u=f (x 1 ,x 2 ,…,xn) — субъективная числовая оценка полезности набора товаров x 1 ,x 2 ,…,xn. Линии уровня для функции полезности называются кривыми безразличия, поскольку ни один из соответствующих наборов товаров не имеет преимущества перед другими.
Функция издержек I (Y) =I (y 1 ,y 2 ,…,yn) — зависимость издержек в стоимостной форме от объемов y 1 ,y 2 ,…,yn выпускаемой продукции.
Производственная функция Y=f (x 1 ,x 2 ,…,xn) — зависимость объема или стоимости выпускаемой продукции от объемов x 1 ,x 2 ,…,xn перерабатываемых ресурсов. Линии уровня производственной функции называются изоквантами.
В экономической литературе часто используется производственная функция Кобба-Дугласа, которая является функцией двух переменных  , где z — объем выпущенной продукции, K — объем основных фондов, L — объем трудовых ресурсов,
, где z — объем выпущенной продукции, K — объем основных фондов, L — объем трудовых ресурсов,  — определенные постоянные,
— определенные постоянные,  .
.
В дальнейшем будем подробно рассматривать функции двух переменных, поскольку все определения и теоремы могут быть обобщены на функции трех и более переменных.
Дифференциальное исчисление функции нескольких переменных
Предел функции нескольких переменных. Непрерывность функции
Определение 5.12. Число А называется пределом функции  при
при  и
и  (или в точке
(или в точке  ), если для любого, сколь угодно малого положительного числа
), если для любого, сколь угодно малого положительного числа  , найдется окрестность точки
, найдется окрестность точки  , такая, что для всех точек
, такая, что для всех точек  из этой окрестности, быть может за исключением точки
из этой окрестности, быть может за исключением точки  , выполняется неравенство
, выполняется неравенство  .
.
Обозначается предел так:  или
или  .
.
Определение 5.13. Функция z=f (x, y) называется непрерывной в точке P 0(a, b), если  f (x, y)= f (a, b) или
f (x, y)= f (a, b) или  f (a, b).
f (a, b).
Замечание. Функция  будет непрерывной в точке
будет непрерывной в точке  , если она:
, если она:
1) определена в точке  ;
;
2) имеет конечный предел при  и
и  ;
;
3) этот предел равен значению функции в точке  , т.е.
, т.е. 
Определение 5.14. Функция называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.
Функции двух и большего числа переменных, непрерывные в замкнутой ограниченной области, обладают свойствами, аналогичными свойствам функций одной независимой переменной, непрерывных на отрезке. Например, имеет место следующая теорема.
Теорема. Если функция z=f (P) непрерывна в ограниченной замкнутой области, то она в этой области:
1) ограничена, т.е. существует N=const такая, что для всех точек из этой области выполняется:  ;
;
2) имеет наименьшее m и наибольшее M значения;
3) принимает хотя бы в одной точке области любое численное значение, заключенное между m и M.
Частные производные
Пусть на некотором множестве D определена функция z=f (P). Возьмем произвольную точку P (x, y)  D и придадим переменной x произвольное приращение
D и придадим переменной x произвольное приращение  , оставляя значение переменной у неизменным. При этом
, оставляя значение переменной у неизменным. При этом  таково, что точка (x+
таково, что точка (x+  , y)
, y)  D. Тогда соответствующее приращение функции
D. Тогда соответствующее приращение функции
 z=f (x+
z=f (x+  , y)– f (x, y)
, y)– f (x, y)
называется частным приращением функциипо переменной x в точке P (x, y). Аналогично определяется частное приращение функции по переменной у:
 z=f (x, y+
z=f (x, y+  )– f (x, y).
)– f (x, y).
Определение 5.15. Если существует конечный предел  , то он называется частной производной функции z=f (x, y) в точке P (x, y) по переменной х и обозначается
, то он называется частной производной функции z=f (x, y) в точке P (x, y) по переменной х и обозначается
 .
.
Аналогично определяется частная производная функции z=f (x, y) по переменной у:
 .
.
Частные производные так же обозначаются  или
или  ,
,  .
.
Из определения 5.15 следует, что частная производная функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении второй переменной. Поэтому вычисление частных производных производится по формулам и правилам нахождения производных функций одной переменной.
Рассмотрим примеры вычисления частных производных.
Пример 5.4. Найти частные производные  функции
функции
 .
.
Решение. 

Пример 5.5. Найти частные производные  функции
функции 
Решение.


Пример 5.6. Пусть производственная функция z=F (K, L) выражает зависимость объема выпущенной продукции от факторов производства: K — объема основных фондов либо в стоимостном, либо в количественном выражении, L — объема трудовых ресурсов (число рабочих, число человеко-дней и т.д.).
Основными экономико-математическими характеристиками производственной функции являются: средняя производительность труда  ; средняя фондоотдача
; средняя фондоотдача  .
.
Наряду со средними показателями при анализе производственных функций играют роль и предельные характеристики функций.
Предельная производительность труда  характеризует величину дополнительного эффекта от каждой дополнительной единицы затраченного труда в данной точке (K, L).
характеризует величину дополнительного эффекта от каждой дополнительной единицы затраченного труда в данной точке (K, L).
Для производственной функции Кобба-Дугласа  имеем:
имеем:  , т.е. предельная производительность труда пропорциональна средней производительности.
, т.е. предельная производительность труда пропорциональна средней производительности.
Аналогично определяется предельная фондоотдача  .
.
Применяемые в экономических исследованиях относительные производные (эластичности) для функции Кобба-Дугласа равны 
Пример 5.7. На предприятии с объемом фондов 10 млрд. грн., количеством работников 1000 человек запланировано повышение выпуска продукции на 3%, для этого необходимо увеличить объем фондов на 6% или количество работников на 9%. Найти выражение функции Кобба-Дугласа, среднюю фондоотдачу и предельную фондоотдачу, если в 2000 году один работник производил за год продукции на 1 млрд. грн.
Решение. Из условия следует, что 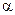 =3/6=1/2,
=3/6=1/2,  =3/9=1/3, таким образом
=3/9=1/3, таким образом  . Подставляя данные условия, получим уравнение 106×1000 =А ×(1010)1/2×(1000)1/3. Следовательно, А= 1000 и
. Подставляя данные условия, получим уравнение 106×1000 =А ×(1010)1/2×(1000)1/3. Следовательно, А= 1000 и  . Средняя фондоотдача
. Средняя фондоотдача 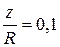 , предельная фондоотдача
, предельная фондоотдача 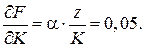
Полный дифференциал
Определение 5.16. Полным приращением функции z=f (P) в точке P (x, y), соответствующим приращениям  и
и 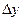 переменных x и y называется выражение
переменных x и y называется выражение
Δz=f(x+  ,y+
,y+ 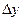 )–f(x,y). (5.1)
)–f(x,y). (5.1)
Полное приращение функции, вообще говоря, не равно сумме частных приращений, т. е.  .
.
Определение 5.17. Функция z=f (P) называется дифференцируемой в точке P (x, y), если ее полное приращение (5.1) в этой точке может быть представлено в виде
Δz=A  +B
+B 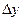 +α(
+α( ,
, 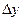 )
)  +β(
+β( ,
, 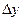 )
)  ,
,
где A и B не зависят от  и
и 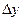 , а α(
, а α( ,
, 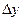 ) и β(
) и β( ,
, 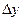 ) — бесконечно малые функции при
) — бесконечно малые функции при  → 0,
→ 0, 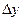 → 0 (т.е.
→ 0 (т.е.  ).
).
Теорема 1. (Необходимое условие дифференцируемости). Если функция z=f (P) дифференцируема в точке P (x, y), то она имеет в этой точке частные производные fx´ (x, y) и fy´ (x, y), причем fx´ (x, y)= A, fy´ (x, y)= B.
Теорема 2. (Достаточное условие дифференцируемости). Если функция z=f (P) имеет частные производные в некоторой окрестности точки P (x, y) и эти производные непрерывны в самой точке P (x, y), то эта функция дифференцируема в точке P (x, y).
Замечание. Понятие дифференцируемости для функции трех и более переменных вводится аналогично понятию, рассмотренному для функции двух переменных.
Определение 5.18. Дифференциалом dz дифференцируемой в точке P (x, y) функции z=f (P) называется линейная относительно приращений  и
и  часть полного приращения этой функции, т.е.
часть полного приращения этой функции, т.е.
dz = A  +B
+B 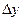 . (5.2)
. (5.2)
Используя теорему 1, выражение (5.2) можно записать следующим образом
dz = fx´ (x, y)  +fy´ (x, y)
+fy´ (x, y) 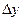 . (5.3)
. (5.3)
Если положить z=x, то dz=dx= 1  + 0
+ 0 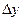 , т.е. dx=
, т.е. dx=  , аналогично dy=
, аналогично dy=  и дифференциал (5.3) можно записать как
и дифференциал (5.3) можно записать как
dz = fx´ (x, y) dx+fy´ (x, y) dy.
Таким образом, полный дифференциал функции  вычисляется по формуле
вычисляется по формуле

или
 (5.4)
(5.4)
Аналогично полный дифференциал функции трех аргументов  вычисляется по формуле
вычисляется по формуле 
Замечание. Из определения следует, что  . Этим широко пользуются в приближенных вычислениях, т.к. дифференциал обычно легче подсчитать, чем полное приращение.
. Этим широко пользуются в приближенных вычислениях, т.к. дифференциал обычно легче подсчитать, чем полное приращение.
Пример 5.8. Дана функция  . Найти dz.
. Найти dz.
Решение.


Следовательно,
 .
.
Пример 5.9. Найти полное приращение и полный дифференциал функции  при изменении
при изменении  от точки
от точки 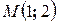 до точки
до точки  .
.
Решение.

 ;
;


Очевидно, что  .
.
Пример 5.10. Вычислить приближенно 
Рассмотрим функцию z=xу.

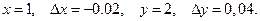

Вычисление с помощью калькуляторадает следующий результат 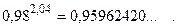
ЛИТЕРАТУРА
Для содержательных модулей
1. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. — М.: Наука, 1988.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.