Лекция 17
Числовые ряды. Признаки сходимости рядов.
Вопросы:
1. Понятие числового ряда.
2. Сходимость ряда.
3. Необходимый признак сходимости ряда.
4. Достаточные признаки сходимости знакоположительных рядов:
а) признаки сравнения;
б) признак Даламбера;
в) радикальный признак Коши;
г)интегральный признак Коши.
5. Знакопеременные ряды. Абсолютная и условная сходимость рядов.
6. Знакочередующиеся ряды. Признак Лейбница.
7. Функциональные ряды. Область сходимости ряда.
В теоретических исследованиях различных экономических процессов, таких, как определение цены бессрочных акций, величины ренты, оценке эффективности инвестиционных проектов и т.п. используются бесконечные ряды, их суммы. Одним из наиболее актуальных приложений являются временные ряды.
Числовые ряды. пРИЗНАКИ СХОДИМОСТИ РЯДОВ.
Основные понятия. Сходимость ряда
Пусть дана бесконечная числовая последовательность а 1, а 2, …, аn…
Определение 8.1. Числовым рядом называется выражение
 . (8.1)
. (8.1)
Числа а 1, а 2, … — члены ряда, а n — общий член ряда или n -ый член.
Если все члены ряда положительны, то соответствующий ряд — знакоположительный. В зависимости от того, какие знаки имеют члены ряда (8.1), можно рассматривать знакоотрицательные, знакоположительные, знакопеременные ряды. Частным случаем знакопеременных рядов является знакочередующиеся ряды. Например,
1–1+1–1+…+(-1) n +1+…,

Определение 8.2. Частичной суммой ряда (8.1) называется сумма n первых членов ряда:
Sn=a 1 +a 2 +…+an.
Частичные суммы ряда:
S 1 =a 1, S 2 =a 1 +a 2 =S 1 +a 2, S 3 =a 1 +a 2 +a 3 =S 2 +a 3, … Sn=Sn -1 +an,… образуют числовую последовательность, сходимость которой можно исследовать, вычислив ее предел.
Определение 8.3. Если существует конечный предел последовательности частичных сумм  , то говорят, что ряд (8.1) сходится и его сумма равна S.
, то говорят, что ряд (8.1) сходится и его сумма равна S.
Если  не существует или бесконечен, то ряд называется расходящимся и суммы не имеет.
не существует или бесконечен, то ряд называется расходящимся и суммы не имеет.
В школьном курсе математики рассматривались геометрические прогрессии.
Геометрической прогрессией называется ряд
a+aq+aq 2 +…+aqn- 1 +…, a≠ 0.
Сумма первых членов  .
.
Если │ q │<1, то  и, следовательно,
и, следовательно,
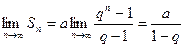 .
.
Таким образом, при │ q │<1 бесконечная геометрическая прогрессия представляет собой сходящийся числовой ряд, сумма которого  .
.
Если q >1, то  и, следовательно,
и, следовательно,  , то есть ряд расходится.
, то есть ряд расходится.
Если q <-1, то  не существует.
не существует.
При q= 1 получим ряд: a+a+a+…a+…, тогда  при
при  и, следовательно, ряд расходится.
и, следовательно, ряд расходится.
При q=- 1 получим тоже расходящийся ряд: a-a+…+ (-1) na+…
Вывод: бесконечная геометрическая прогрессия представляет собой ряд, который сходится при │ q │< 1 и расходится при │ q │≥ 1.
Пример 8.1. С помощью определения сходимости исследовать сходимость гармонического ряда: 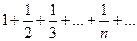
Предположим, что этот ряд сходится и его сумма равна S. Тогда по свойствам пределов 
Но  , каждое слагаемое, кроме последнего, в этой сумме больше или равно
, каждое слагаемое, кроме последнего, в этой сумме больше или равно  , следовательно:
, следовательно:
S2n-Sn>n  =
=  , значит, равенство
, значит, равенство  не выполняется.
не выполняется.
Таким образом, гармонический ряд является расходящимся рядом.
Свойства сходящихся рядов
Рассмотрим простейшие теоремы.
Пусть имеем ряд
a 1 +a 2 +…+an+… + an+ 1 +…+an+m+… (8.2)
Если в ряде (8.2) отбросить первые n членов, то получится ряд, который называется остатком ряда (8.2) после n– го члена и обозначается через rn, то есть:
rn=an+ 1 +an+ 2 +…+an+m+… (8.3)
Теорема 1. Если ряд (8.2) сходится, то сходится и его остаток, и, наоборот, если сходится остаток, то сходится и ряд
Доказательство. Пусть сходится ряд (8.2), докажем, что сходится и его остаток (8.3).
Запишем частичную сумму первых n+m членов ряда:
Sn+m=Sn+(an+ 1 +an+ 2 +…+an+m) (8.4)
Зафиксируем номер n и пусть m→∞, тогда предел левой части равенства (8.4) по условию существует и равен сумме S ряда. В правой части предел первого слагаемого Sn есть само это число, так как частичная сумма Sn постоянна при фиксированном n, следовательно, предел второго слагаемого при m→ ∞ также конечный, т.е. остаток сходится и его сумма равна rn. Таким образом,
S=Sn+rn, ч.т.д.
Рассмотрим два числовых ряда:
a 1 +a 2 +…+an+… (8.5)
b 1 +b 2 +…+bn+ … (8.6)
Определение 8.4. Ряд
(a 1 +b 1) + (a 2 +b 2) +…+ (an+bn) +… (8.7)
называется суммой рядов (8.5) и (8.6).
Определение 8.5. Если k — число, то ряд
ka 1 +ka 2 +…+kan+… (8.8 )
называется произведением ряда (8.5) на число k.
Теорема 2. Если ряды (8.5) и (8.6) сходятся, А и В соответственно их суммы, то ряд (8.7) также сходится и его сумма равна А+В.
Теорема 3. Если ряд (8.5) сходится и его сумма равна А, то ряд (8.8) сходится и его сумма равна kА.
Доказательство.
Пусть  и
и  , а
, а 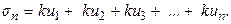 Тогда
Тогда  и
и  что и требовалось доказать.
что и требовалось доказать.