Тема: Геометрические построения, необходимые при выполнении чертежей (Деление отрезков, углов и окружностей на равные части)
Ход урока
I. Объяснение нового материала
Деление отрезков прямых на равные части
-на 2 части выполняется в следующей последовательности.
Из концов отрезка АВ циркулем проводят 2дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках 1и 2. Точки 1и 2 соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок АВ на 2 равные части.
- деление отрезка прямой на любое число равных частей.
Пусть отрезок АВ требуется разделить на 7 равных частей. Для этого из любого конца отрезка, например из т.В проводят под любым острым углом вспомогательную прямую линию ВС, на которой от т.В измерительным циркулем откладывают 7 равных отрезков произвольной величины. Крайнюю точку 7части соединяют с т. А отрезкомАВ. Затем с помощью линейки и угольника проводят прямые параллельно отрезку А7, которые и разделяют отрезок АВ на 7 равных частей.
Деление углов на равные части
-любой острый угол на 2 части.
Из вершины угла провести произвольным радиусом R дугу до пересечения со сторонами угла ВАС в точках 1 и 2. Из полученных точек проводят две дуги этим же радиусом R до взаимного пересечения в т.3. Вершину угла соединяем с т.3 прямой, которая делит угол пополам. Эта прямая называется биссектрисой.
-деление тупого угла на 4 равные части.
Повторяя это построение с полученными углами, угол можно разделить на 4 равные части.
-деление прямого угла на 3 равные части.
Из вершины А прямого угла произвольным радиусом R описываем дугу окружности до пересечения ее со сторонами прямого угла в точках 1и 2, из которых проводят дуги окружности того же радиуса R до пересечения с дугой в точках 3 и 4. Точки 3 и 4 соединяем с вершиной угла А прямыми и получаем стороны А 3 и А 4, которые делят угол на 3 равные части.
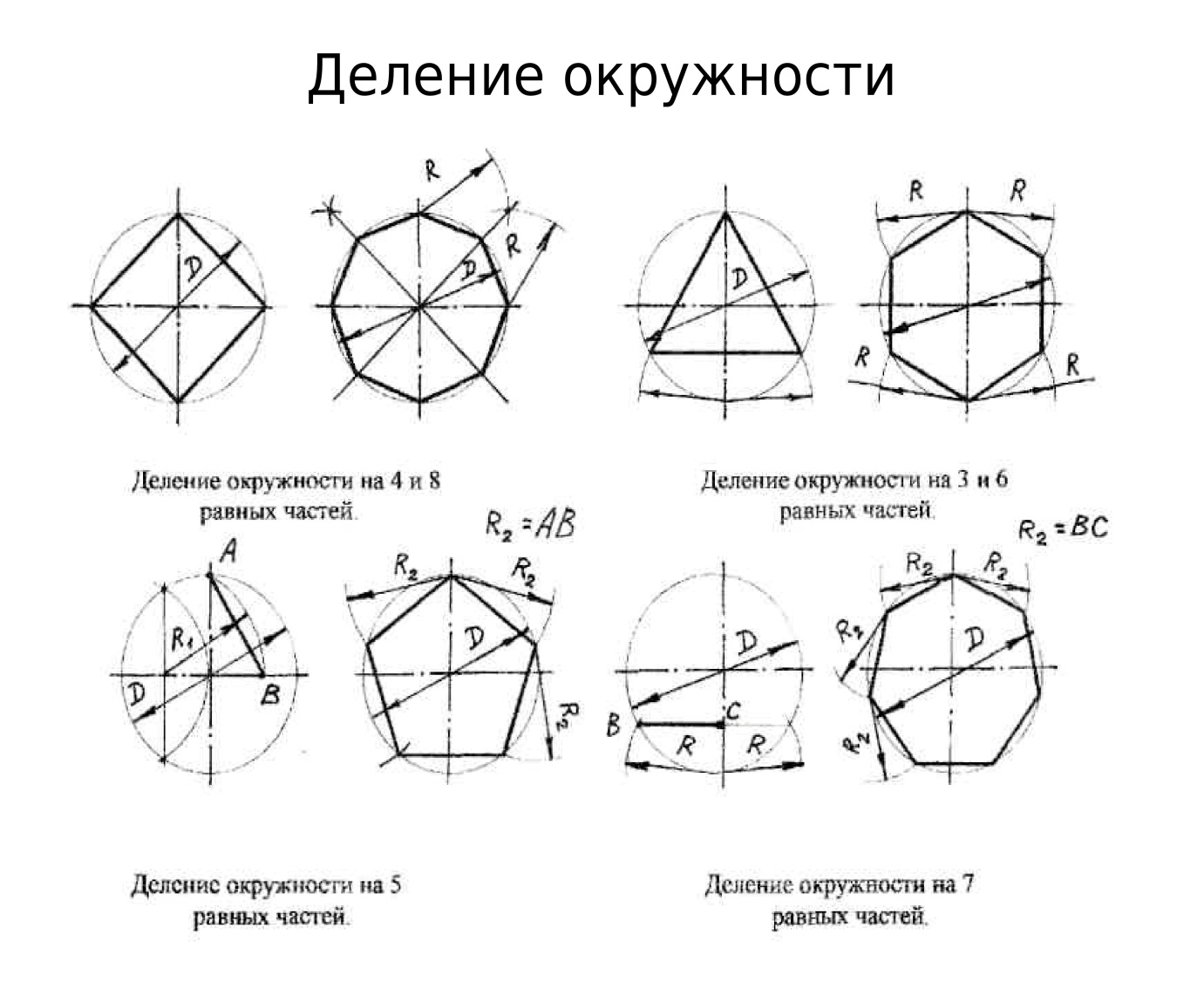
Деление окружности на 3, 6 и 12 равных частей.
Для нахождения точек, делящих окружность радиусом R20 на 3 равные части, нужно из нижней точки пересечения осевой линии и окружности, провести дугу радиусом R20. Пересечения дуги с окружностью дают 2 точки 1 и 2; третья точка деления будет находиться в верхней точке пересечения оси и окружности(3). Соединив три точки, получим вписанный треугольник.
Деление окружности на 6 равных частей выполняем так же, но дугу описываем не один, а 2 раза, из верхней и нижней точки пересечения осевой линии и окружности радиусом R20, равным радиусу окружности.
При делении окружности на 12 равных частей с помощью циркуля можно
использовать тот же прием, что и при делении окружности на 6 равных частей, но дуги радиусом R20 описывать 4 раза из точек пересечения центровых линий и окружности.
4. Деление окружности на 4 и 8 равных частей.
Сначала проводим 2 перпендикулярные оси. Из т.О, пересечения осей проводят окружность R20, которую нужно разделить на 8 равных частей.
Точки 1, 3, 5, и 7 деления окружности на 4 части получаем на пересечении осевых линий с окружностью. Для получения т. 2, 4, 6,8, применяем прием деления прямого угла на 2 равные части при помощи циркуля.
Деление окружности на 5 частей
Проводим центровые штрихпунктирные линии. Из центра пересечения осевых линий т.О, проводим окружность радиусом R 20. Из боковой точки пересечения осевой линии и окружности, этим же радиусом проводим дугу. Получаем две точки пересечения дуги и окружности т. А и В, которые соединяем отрезком. На пересечении этого отрезка и осевой линии, получаем т.1, которую соединяем с т.2 (верхняя точка пересечения осевой линии и окружности). Затем радиусом R1, 2 проводим дугу до пересечения с осевой линией, получим т.3. Циркулем измеряем расстояние от т.2 до т.3, Это и будет сторона пятиугольника. Ставим ножку циркуля в т.2 и этим радиусом делаем две засечки и из полученных точек делаем еще две засечки. Получаем пять точек, которые соединяем и получаем вписанный пятиугольник.
Деление окружности на 7 равных частей.
Из нижней точке пересечения осевой линии и окружности проводим вспомогательную дугу радиусом R, равным радиусу окружности, которая пересечет окружность в т.1 и 2. Этот отрезок пересечет вертикальную осевую линию в т.3. Отрезок 1-3 и будет стороной семиугольника. Из вертикальной точки пересечения осевой линии и окружности, радиусом R1,3, делаем по окружности 7 засечек и получаем 7 искомых точек, которые соединяем между собой и получаем вписанный семиугольник.
Итак, геометрические построения - это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.
Домашнее задание
Вычертить одну из деталей с применением деление окружностей
