Определение
Число  называется пределом числовой последовательности
называется пределом числовой последовательности  , если последовательность
, если последовательность  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.
, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

5.
Пусть функция y =f (x) определена в некоторойокрестности x0, кроме, может быть, самой точки x0.
Определение. Число A называется пределом функцииy =f (x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε > 0найдетсятакоечисло δ > 0, что для всех х ¹x0, удовлетворяющих неравенству
│ х –x0 │< δ, выполняется неравенство│ f (x) – А │<ε.
Или кратко:
 ε > 0
ε > 0  δ > 0,
δ > 0,  x:│ х –x0 │< δ, х ¹x0 => │ f (x) – А │<ε.
x:│ х –x0 │< δ, х ¹x0 => │ f (x) – А │<ε.

Геометрический смысл предела функции заключается в следующем: число  , если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f (x) лежат в ε – окрестности точки А.
, если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f (x) лежат в ε – окрестности точки А.
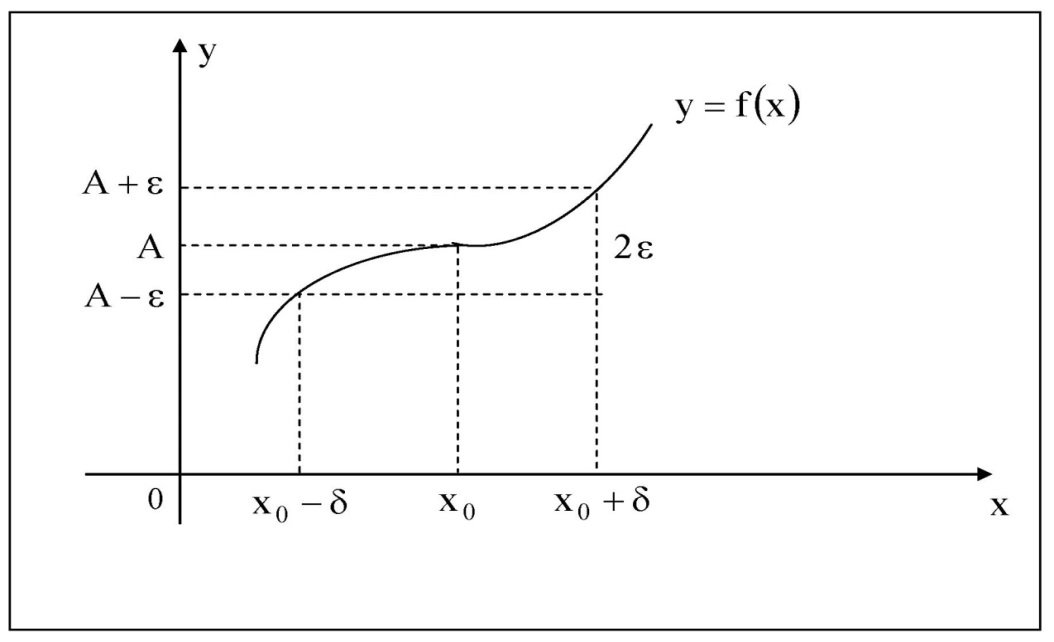
Рис. 1
Пример: Доказать, что

Решение. Возьмем произвольное  и найдем
и найдем  такое, что для всех x, удовлетворяющих неравенству,
такое, что для всех x, удовлетворяющих неравенству,  , выполняется неравенство
, выполняется неравенство  , то есть
, то есть  .
.
Взяв  , видим, что для всех x, удовлетворяющих неравенству,
, видим, что для всех x, удовлетворяющих неравенству,  , выполняется неравенство
, выполняется неравенство  , следовательно,
, следовательно,

Пусть функция y =f (x) определена в промежутке (– 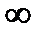 ; +
; + 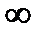 ).
).
Определение. Число A называется пределом функцииf (x) при х 
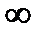 , если для любого числа ε > 0существуеттакоечисло M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │ x │ >M,выполняется неравенство │ f (x) – А │< ε. В этом случае пишут
, если для любого числа ε > 0существуеттакоечисло M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │ x │ >M,выполняется неравенство │ f (x) – А │< ε. В этом случае пишут  f (x) = А.
f (x) = А.
Или кратко:
 ε > 0
ε > 0  M > 0, │ x│ > M => │ f (x) – А │<ε.
M > 0, │ x│ > M => │ f (x) – А │<ε.
 f (x) = А.
f (x) = А.
6. тет
7.
Сравнивая между собой определения предела функции в точке с определением бесконечно малой функции, можно заметить, что разность между функцией и ее пределом является величиной бесконечно малой.
Утверждение этого факта формулируют в двух теоремах − прямой и обратной.
Теорема (прямая).
Если функция 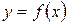 имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции
имеет предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции  , т.е. если
, т.е. если 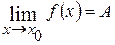 , то
, то
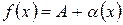 .
.
 может принимать как положительные, так и отрицательные значения, т.е. функция
может принимать как положительные, так и отрицательные значения, т.е. функция  может быть как больше, так и меньше своего предела.
может быть как больше, так и меньше своего предела.
8.
1. Сумма бесконечно больших величин одного знака есть величина бесконечно большая того же знака.
2. Произведение бесконечно больших величин есть величина бесконечно большая.
3. Произведение бесконечно большой величины на функцию, предел которой не равен нулю(или на постоянную величину) есть величина бесконечно большая.
4. Сумма бесконечно большой величины и ограниченной величины есть величина постоянно большая.
5. Частное от деления величины бесконечно большой на функцию, имеющую предел, есть величина бесконечно большая.
9.
Основные теоремы о пределах.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Пример.  .
.
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
 .
.
Следствие 2. Предел степени равен степени предела:
 .
.
Пример.  .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
 , если
, если  .
.
Примеры.
1. 
 .
.
2. 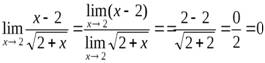 .
.
3. 
10.

11.
Первый замечательный предел: 
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Задание. Найти предел 
Решение. Воспользуемся заменой и первым замечательным пределом.


Ответ. 
Пример
Задание. Найти предел 
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.



Ответ. 