Уравнение прямой, имеющей угловой коэффициент k и проходящей через точку M (х 1; у 1), записывается в виде (пучок прямых) 
. Перепишем это уравнение в виде 
.
Обозначим 
и получим уравнение прямой
(2.15)
которое называется уравнением прямой c угловым коэффициентом (Рис. 2.14, 2.15).
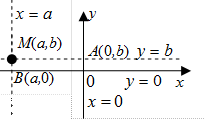
Рис. 2.14, Рис. 2.15 Рис. 2.16
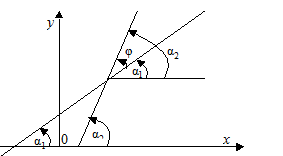
Угол между двумя прямыми. Взаимное расположение двух прямых на плоскости
Пусть заданы две прямые 
и требуется определить угол 
между ними. Из чертежа видно, что 
причем 
Если 
, то
или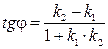 
, (2.16)
где стрелка означает, что угол 
получается поворотом прямой (1) к прямой (2) против часовой стрелки. Если хотя бы одна из прямых вертикальна, то можно находить угол между прямой и осью Ох или находить угол между двумя векторами и т. д. Если прямые 
и 
параллельны, то 
и 
откуда из формулы 
т. е. параллельности прямых имеет вид
. (2.17)
И наоборот, если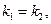 
то 
, т. е. прямые параллельны.
Если прямые перпендикулярны, то 
или 
Отсюда 
(2.18)
Рис. 2.17
Справедливо также и обратное утверждение.
Если прямые заданы общими уравнениями 
и 
, то
(2.19)
и условие параллельности прямых принимает вид
(2.20)
а условие перпендикулярности прямых принимает вид
или 
(2.21)
а если 
то прямые совпадают.
Пример 2.6. Составить уравнения прямых, проходящих через точку М (-2;-5) параллельной, перпендикулярной прямой 
и под углом 
к ней.
Решение. Разрешив последнее уравнение относительно у, получим 
Следовательно угловой коэффициент данной прямой равный 
. В силу условия параллельности прямых 
угловой коэффициент параллельной прямой также равен 
, а в силу условия перпендикулярности 
прямых угловой коэффициент перпендикулярной прямой равен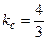 
. Из формулы (2.16) 
Кроме того 
. Поэтому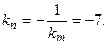 
Воспользовавшись уравнениям (2.12), получаем 
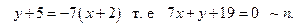
Рис. 2.18
2.2.9. Расстояние от точки до прямой
Пусть даны точка 
и прямая 
Рис. 2.19
Определение 2.11. Под расстояниемd от точки М 0 до прямой АВ понимается длина перпендикуляра M 0 D, опущенного
из точки M 0 на прямую АВ. Расстояние 
равно модулю проекции вектора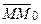 
на вектор 
. Поэтому 
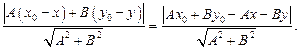
Из уравнения прямой 
Поэтому
(2.22)
Пример 2.7. Найти расстояние между параллельными прямыми 
и 
.
Решение. Возьмем на одной из прямых, например на прямой 
произвольную точку Е (12,0). Тогда искомое расстояние равно расстоянию от точки Е до прямой 
: 
.
Общее уравнение прямой (области, задаваемые линейными неравенствами)
Неравенство 
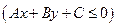определяет полуплоскость на плоскости 
Чтобы определить эту полуплоскость надо: 1) построить прямую 
2) взять произвольную точку, не лежащую на этой прямой; 3) подставить координаты этой точки в левую часть неравенства; 4) если неравенство в этой точке выполняется, то оно определяет полуплоскость в которой лежит эта точка, если же не выполняется, то неравенство определяет другую полуплоскость.
Примеры
Пример 2.8. Даны уравнения сторон треугольника 
1) Составить уравнение высоты, проведенной из точки А; 2) Найти точку пересечения высот; 3) Составить уравнение медианы, проведенной из точки В; 4) Найти точку пересечения медиан; 5) Найти угол А; 6) Записать систему неравенств, определяющую треугольник АВС. Сделать чертеж.
Решение. Найдем координаты вершин треугольника. Координаты точки А находятся решением системы
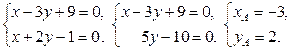
Аналогично находим 
Пусть N — точка пересечения высот, M — точка пересечения медиан, D — середина АС.
Рис. 1.20
1. Для нахождения высоты воспользуемся уравнением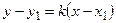 
. 
. Из условия перпендикулярности прямых 
.
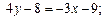
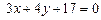2. Для нахождения точки пересечения высот найдем, аналогично, уравнение еще одной высоты, например 
, и найдем точку их пересечения N. 
3. Найдем координаты точки D, делящей отрезок AC пополам 
.. Точка D(0;1/2). Так как прямая BD лежит на оси ОУ, то уравнение медианы BD: 
4. Точка M делит отрезок BD в отношении 
Поэтому 
Точка М (0;4/3).
5. 
, 
6. Чтобы записать треугольник с помощью неравенств, возьмем произвольную точку внутри треугольника, например 
и подставим ее координаты в левые части уравнений сторон. Полученным неравенствам будет соответствовать система неравенств, определяющая треугольник. 
Пример 2.9. Законы спроса и предложения на некоторый товар определяются уравнениями
Требуется:
a) Найти точку рыночного равновесия.
b) Найти точку равновесия после введения налога, равного 3. Найдите увеличение цены и уменьшение равновесного объема продаж.
c) Какая субсидия приведет к увеличению объема продаж на 2 единицы?
d) Вводится пропорциональный налог, равный 20%. Найдите новую точку равновесия и доход правительства.
e) Правительство установило минимальную цену, равную 7. Сколько денег будет израсходовано на скупку излишек?
Решение. Обозначим: D — закон спроса; S — закон предложения; х — количество товара; 
— общая цена товара на рынке; 
— цена товара, получаемая поставщиками; t — налог на товар; s — субсидия на товар.
a) Используя равенство между ценой спроса и ценой предложения 
находим точку равновесия М:
Точка 
является точкой равновесия (Рис. 2.21).
b) Если введен налог 
то система уравнений для определения новой точки равновесия примет вид
Рис. 2.21
Используя соотношение между ценой на рынке 
и ценой 
получаемой поставщиками, имеем следующую систему для определения точки рыночного равновесия
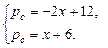
Решая эту систему, получаем новую точку равновесия 
Следовательно, после введения налога равновесная цена увеличилась на 2 единицы, а равновесный объем уменьшился на 1 единицу.
с) Если представлена субсидия, то система уравнений для определения точки равновесия имеет вид
Новый объем продаж равен 5 единицам (5+3). Подставляя 
в систему, находим:
.
d) Если налог составляет 20%, то вся рыночная цена составляет 120%, из них 100% получают поставщики товара, а 20% — государство. Итак, поставщики получают
Уравнения спроса остаются неизвестными, а уравнение предложения подставляем 
Решая эту систему, находим новую точку равновесия 
Очевидно, что доход правительства R равен площади заштрихованного прямоугольника 
d) Если установлена минимальная цена, то из уравнений спроса и предложений можно найти объемы спроса и предложения. Разницу между ними скупает правительство. Так как 
то 
Затраты правительства составят 
ЛИТЕРАТУРА
Для содержательных модулей
1. Ефимов Н.В. Краткий курс аналитической геометрии. — М.: Наука, 1979.
2. Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, 1978.
3. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. — М.: Наука, 1968.
3. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1967.