Первичная статистическая обработка экспериментальных данных
Основной задачей предварительной обработки экспериментальных данных является их систематизация (таблицы, карточки, графики), определение диапазона изменения функции и аргумента, их средних значений и частотных характеристик. К первичной обработке также относятся исключение грубых ошибок, оценка точности измерений, расчет доверительного интервала и подбор эмпирических формул (коэффициентов) по графическим зависимостям. Для нахождения зависимостей между исследуемыми параметрами по экспериментальным данным строят графики.
Определение грубых ошибок измерений
Проведение различных физико-химических исследований связано с набором массивов экспериментальных данных, которые могут содержать грубые ошибки (промахи). Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
- неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
- неправильная запись результата наблюдений, например, значений отдельных мер использованного набора гирь;
- хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Их необходимо исключить, предварительно убедившись, что это действительно ошибки. Чаще всего для решения подобной задачи используется критериальная оценка.
1. Грубые ошибки можно обнаружить с помощью критерия Шовене, используя следующую схему:
а) выделить из массива «сомнительные» измерения, т.е. те, которые явно выпадают из серии;
б) рассчитать среднеарифметическое значение в серии по уравнению:
 ;
;
в) рассчитать среднеквадратическую погрешность данной серии по уравнению:
 ,
,
где  ;
;
г) найти предельную остаточную погрешность первичных измерений данной серии:
 ,
,
где Zn – критерий Шовене (см. табл.1)
д) сравнить  с каждым единичным значением
с каждым единичным значением  и определить промахи (промахом считается
и определить промахи (промахом считается  , для которого
, для которого  >
>  ).
).
Таблица 1. Значения критерия Шовене
| n | Zn | n | Zn | n | Zn | n | Zn | n | Zn |
| 1,68 | 1,89 | 2,16 | 2,31 | 2,58 | |||||
| 1,73 | 1,96 | 2,20 | 2,36 | 2,80 | |||||
| 1,79 | 2,03 | 2,26 | 2,39 | 2,92 | |||||
| 1,86 | 2,10 | 2,28 | 2,50 | 3,29 |
Если промахи обнаруживаются, то соответствующее значение  отбрасывается, и проводят новое обнаружение промахов. Допускается только исключение одного промаха в серии. Если промахов обнаружено больше одного, то вся серия считается недействительной и измерения необходимо повторить.
отбрасывается, и проводят новое обнаружение промахов. Допускается только исключение одного промаха в серии. Если промахов обнаружено больше одного, то вся серия считается недействительной и измерения необходимо повторить.
Пример 1. В результате испытаний образцов металлизированных окатышей при выдержке в окислительной атмосфере в течение 72 часов получили степень окисления (%): 30,7; 40,3; 34,1; 34,8; 36,0; 33,5; 34,8; 37,9; 36,2; 34,0.
Решение. Результат 40,3 кажется завышенным. Для проверки рассчитываем среднеарифметическое значение и среднеквадратическую погрешность данной серии, результат расчета представлен в таблице 2.
Таблица 2. Результаты расчета
| Номер опыта | 
| 
| 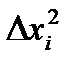
|
| 30,7 | -4,53 | 20,5209 | |
| 40,3 | 5,07 | 25,7049 | |
| 34,1 | -1,13 | 1,2769 | |
| 34,8 | -0,43 | 0,1849 | |
| 0,77 | 0,5929 | ||
| 33,5 | -1,73 | 2,9929 | |
| 34,8 | -0,43 | 0,1849 | |
| 37,9 | 2,67 | 7,1289 | |
| 36,2 | 0,97 | 0,9409 | |
| -1,23 | 1,5129 | ||
Среднее 
| 35,23 | Сумма | 61,041 |

| 2,604 |
Для определения остаточной погрешности воспользуемся таблицей 1. Для исследуемой серии опытов из 10 измерений Zn = 1,96, тогда fnp.n = Zn·Sn = 2,604∙1,96 = 5,104.
Сравнивая fnp.n с 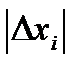 , приходим к выводу, что промахов нет, т.к. согласно расчету для проверяемого результата 40,3
, приходим к выводу, что промахов нет, т.к. согласно расчету для проверяемого результата 40,3  = 5,07, и это значение меньше, чем полученное fnp.n. Т.о. все значения в серии опытов должны быть оставлены.
= 5,07, и это значение меньше, чем полученное fnp.n. Т.о. все значения в серии опытов должны быть оставлены.
Задание.
С помощью программы Excel провести проверку на наличие промаха по критерию Шовене для указанных экспериментальных результатов.
1. Микрометром были произведены 7 измерений диаметра стержня (мм): 4,02; 3,98; 3,97; 4,01; 4,05; 4,03, 3,94.
2. В результате определения содержания алюминия в сплаве получены следующие значения (в масс. %): 7,48, 7,49, 7,52, 7,47, 7,50, 7,43, 7,52, 7,49.
2. Грубые промахи можно также «выявить», используя критерий Романовского β:
 ,
,  ,
,
где xmax и xmin – наибольшие и наименьшие значения из проделанных измерений. При этом для расчета  и Sn подозрительный результат не используется.
и Sn подозрительный результат не используется.
Максимальное значение критерия β (β max), возникающее вследствие статистического разброса, определяется по таблице 3 в зависимости от значения доверительной вероятности p и числа измерений без учета подозрительных результатов N = n-k.
Таблица 3. Значения критерия βmax
| N | βmax при p | N | βmax при p | ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| 1,41 | 1,41 | 1,41 | 2,38 | 2,55 | 2,87 | ||
| 1,64 | 1,69 | 1,72 | 2,40 | 2,58 | 2,90 | ||
| 1,79 | 1,87 | 1,96 | 2,43 | 2,60 | 2,93 | ||
| 1,89 | 2,00 | 2,13 | 2,45 | 2,62 | 2,96 | ||
| 1,97 | 2,09 | 2,26 | 2,47 | 2,64 | 2,98 | ||
| 2,04 | 2,17 | 2,37 | 2,49 | 2,66 | 3,01 | ||
| 2,10 | 2,24 | 2,46 | 2,50 | 2,68 | 3,03 | ||
| 2,15 | 2,29 | 2,54 | 2,52 | 2,70 | 3,05 | ||
| 2,19 | 2,34 | 2,61 | 2,54 | 2,72 | 3,07 | ||
| 2,23 | 2,39 | 2,66 | 2,61 | 2,79 | 3,16 | ||
| 2,26 | 2,43 | 2,71 | 2,67 | 2,85 | 3,22 | ||
| 2,30 | 2,46 | 2,76 | 2,72 | 2,90 | 3,28 | ||
| 2,33 | 2,49 | 2,80 | 2,76 | 2,95 | 3,28 | ||
| 2,35 | 2,52 | 2,84 | 2,80 | 2,99 | 3,37 |
Если β 1 > β max, то xmax следует исключить из расчета как промах.
Если β 2 > β max – исключают значение xmin.
Критерий ненадежен применительно к очень малым выборкам (n <5), а также его бессмысленно применять, если в серии из 3 значений есть два совпадающих, в серии из 4 значений – три совпадающих и так далее. В этом случае тест всегда укажет на необходимость исключения выпадающего значения, как бы мало оно ни отличалось от других.
Пример 2. На цементном заводе в процессе производства ежедневно в течение 45 дней брались пробы и определялось среднее сопротивление сжатию контрольных кубов (Н/см2 или кг/см2). Результаты измерений: 40, 33, 75, 18, 62, 33, 38, 69, 65, 100 (всего 10 опытов).
Решение. Считаем значение 18 экстремальным и рассчитаем среднее арифметическое и среднеквадратическую погрешность без учета этого измерения:  = 57,2; Sn = 22,9.
= 57,2; Sn = 22,9.
Определим значение критерия b для подозрительного результата:

По таблице 3 выбираем значение доверительной вероятности p = 0,99 (при выборе значения р нужно учитывать важность измерений, обычно при расчетах используют р = 0,95, однако если ошибка измерений может привести к тяжелым последствиям, напр. гибели людей, экологической катастрофе, то берется более высокое значение) и для N = 9 находим, что β max = 2,46.
Так как β 2 < β max, делаем вывод, что в данной серии согласно используемому критерию значение 18 не считается промахом и не отбрасывается. Для определения среднего значения измеряемой величины нужно использовать все 10 полученных значений ( = 53,3).
= 53,3).
Задание.
С помощью программы Excel провести проверку на наличие промаха по критерию Романовского для указанных экспериментальных результатов. (Считать р = 0,95.)
1. Результаты измерения напряжения на клеммах батареи составили (В): 0,86; 0,83; 0,87; 0,84; 0,82; 0,95; 0,83; 0,85; 0,89; 0,88.
2. В рабочей зоне производились замеры концентрации вредного вещества. Получен ряд значений (в мг/м3): 12, 16, 15, 14, 10, 20, 16, 14, 18, 14, 15, 17, 23, 16, 21.
3. Критерий “ правило трех сигм ” является одним из простейших для проверки результатов, подчиняющихся нормальному закону распределения. Он используется, когда количество измерений n ≥ 20 … 50. В этом случае считают, что результат, полученный с вероятностью P ≤ 0,003, маловероятен, и его можно квалифицировать как промах, т.е. сомнительный результат xi может быть исключён из измерений, если выполняется условие:
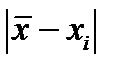 > 3s
> 3s
Среднее арифметическое  и среднеквадратическое отклонение
и среднеквадратическое отклонение  вычисляются без учета экстремальных (вызывающих подозрение) значений
вычисляются без учета экстремальных (вызывающих подозрение) значений  .
.
Однако при бóльших объемах выборки границу цензурирования рекомендуется сдвигать в зависимости от числа проделанных измерений. Так, когда число измерений лежит в диапазоне 50 < n < 100, она равна 4s, при 100 < n < 1000 сдвигается до 4,5s, а при 1000 < n < 10000 ее принимают за 5s.
Задание.
С помощью программы Excel провести проверку на наличие промаха по правилу «трех сигм» для указанных экспериментальных результатов.
Для исследования износа шейки коленчатого вала провели 20 замеров его диаметра микрометром. Получили следующие результаты (в мм): 56,586; 56,588; 56,590; 56,607; 56,590; 56,564; 56,593; 56,588; 56,597; 56,602; 56,592; 56,598; 56,597; 56,601; 56,593; 56,597; 56,603; 56,597; 56,608; 56,577.
4. Критерий Граббса применяется для измерений среднего объема выборки n  50. В таком случае грубой погрешностью считается результат
50. В таком случае грубой погрешностью считается результат  , если значение критерия превышает соответствующее значение
, если значение критерия превышает соответствующее значение 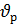 (см. табл. 4), где р – доверительная вероятность.
(см. табл. 4), где р – доверительная вероятность.

При этом расчет  и S проводят по всем имеющимся значениям. Если сомнительное значение является погрешностью, оно должно быть исключено из данных эксперимента и числовые характеристики пересчитаны.
и S проводят по всем имеющимся значениям. Если сомнительное значение является погрешностью, оно должно быть исключено из данных эксперимента и числовые характеристики пересчитаны.
Таблица 4. Критические значения критерия Граббса ( )
)
| n | Доверительная вероятность р | ||
| 0,9 | 0,95 | 0,99 | |
| 1,406 1,645 1,791 1,894 1,947 2,041 2,097 2,146 2,190 2,229 2,264 2,297 2,354 2,404 2,447 2,486 2,521 2,553 2,582 2,609 2,668 2,718 2,762 2,800 | 1,412 1,689 1,869 1,996 2,093 2,172 2,238 2,294 2,343 2,387 2,426 2,461 2,523 2,577 2,623 2,664 2,701 2,734 2,764 2,792 2,853 2,904 2,948 2,987 | 1,414 1,723 1,955 2,130 2,265 2,374 2,464 2,540 2,606 2,663 2,713 2,759 2,837 2,903 2,959 3,008 3,051 3,089 3,124 3,156 3,224 3,281 3,329 3,370 |
5. Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд  . Критерий Диксона определяется как
. Критерий Диксона определяется как

Критическая область для этого критерия КД > Zq. Значения Zq при заданном значении доверительной вероятности р приведены в табл. 5.
Критерий справедлив тогда, когда в выборке присутствует одиночный выброс. Если же есть последовательность выбросов с двумя и более значениями, то критерий может давать положительно ложный результат, если сравниваются два соседних значения с малой разницей, что приводит к занижению КД.
Таблица 5. Значения критерия Диксона
| n | Zq при р, равном | ||
| 0,90 | 0,95 | 0,99 | |
| 0,68 | 0,76 | 0,89 | |
| 0,56 | 0,64 | 0,82 | |
| 0,48 | 0,56 | 0,70 | |
| 0,40 | 0,47 | 0,59 | |
| 0,35 | 0,41 | 0,53 | |
| 0,29 | 0,35 | 0,45 | |
| 0,28 | 0,33 | 0,43 | |
| 0,26 | 0,31 | 0,41 | |
| 0,26 | 0,30 | 0,39 | |
| 0,22 | 0,26 | 0,34 |
Пример 3. При проведении измерительного эксперимента получены следующие значения величины: 11,65; 11,41; 11,57; 11,60; 11,50; 11,55; 11,58; 11,58; 11,61; 11,63. Требуется проанализировать полученные результаты наблюдений в целях выявления грубых погрешностей, используя критерий Диксона.
Решение. Располагаем результаты наблюдений в вариационный возрастающий ряд:
11,41<11,50<11,55<11,57<11,58;11,58<11,60<11,61<11,63<11,65.
По формуле Диксона рассчитываем значение КД: 
Согласно табл. 5 при n=10 и р = 0,95, Zq = 0,41. Значит, полученный ряд результатов не имеет в своем составе грубых погрешностей (КД < Zq). И дальнейшей обработке будет подвергаться весь массив данных наблюдений.
Задание.
Пирометром измеряется температура поверхности нагретого тела. Было проведено шесть измерений, и получены следующие значения (ºС): 950, 930, 990, 1080, 975, 925. Можно ли исходя из критерия Диксона считать значение 1080 ºС грубой погрешностью, полученной, допустим, в результате неправильной регистрации показаний пирометра? (Принять р = 0,95.)
Было произведено восемь измерений расстояний между сваями. Получены следующие результаты: 25,1; 25,2; 24,9; 25,0; 25,2; 25,6; 25,1; 25,2 м. Результат 25,6 м существенно отличается от остальных. Проверить, не является ли он промахом по критерию Диксона.
6. Критерий Ирвина используют при изучении временных рядов, т.е. рядов последовательно расположенных во времени числовых показателей, которые характеризуют уровень состояния и изменения явления или процесса. Он предусматривает сравнение соседних значений полученного ряда данных. Из ряда последовательно выбирают два значения и рассчитывают для них показатель l:

При расчете характеристик сомнительное значение учитывается. В этом методе грубой погрешностью считается результат  , если значение критерия l превышает значение
, если значение критерия l превышает значение  (см. табл. 6). Если погрешность выявлена, результат должен быть исключен и числовые характеристики пересчитаны.
(см. табл. 6). Если погрешность выявлена, результат должен быть исключен и числовые характеристики пересчитаны.
Таблица 6. Критические значения критерия Ирвина ( )
)
| n | Доверительная вероятность р | |
| 0,95 | 0,99 | |
| 2,8 | 3,7 | |
| 2,2 | 2,9 | |
| 1,5 | 2,0 | |
| 1,4 | 1,9 | |
| 1,3 | 1,8 | |
| 1,2 | 1,7 | |
| 1,1 | 1,6 | |
| 1,0 | 1,5 | |
| 0,95 | 1,4 | |
| 0,9 | 1,3 | |
| 0,8 | 1,2 |
Обнаруженное аномальное наблюдение можно заменить расчетным значением, полученным с использованием соседних наблюдений. Самый простой способ замены – расчетное значение есть среднее двух соседних значений. После однократной замены аномальных точек временной ряд все равно может содержать другие аномальные точки. Поэтому процедуру обнаружения и замены аномалий необходимо повторять циклически, до тех пор пока аномальные точки не перестанут обнаруживаться. Так как аномальные точки могут располагаться подряд (блоком), а их замена осуществляется путем усреднения их соседей, то одновременно заменять аномальные точки во всем блоке нецелесообразно. За одну итерацию «проверки-замены» следует заменять только по одной точке в каждом блоке.
Пример. В результате измерения временного ряда получены следующие результаты: 50, 56, 46, 48, 49, 46, 48, 47, 47, 49. Проверить по критерию Ирвина наличие аномальных значений.
Решение. Для каждой пары результатов рассчитаем критерий l: 
Для числа измерений равного n = 10 при доверительной вероятности р = 0,95 полученные значения критерия l не должны превышать λq = 1,5 (см. табл. 6). Сначала по всем 10 значениям рассчитываются среднее арифметическое  = 48,6 и среднее квадратичное отклонение
= 48,6 и среднее квадратичное отклонение  = 2,91.
= 2,91.
Для первой пары значений l2-1 = ç56-50 ç/2,91 = 2,06. Аналогичным образом в зависимости от i = 1, 2 … 10 рассчитываются остальные значения, результаты вычислений представлены в таблице:
| i | ||||||||||
| λ | - | 2,06 | 3,43 | 0,69 | 0,34 | 1,03 | 0,69 | 0,34 | 0,00 | 0,69 |
Из полученных данных видно, что аномально большие значения l, превышающее допустимое, наблюдаются в случае i = 2. Так что число 56 в данном ряду следует рассматривать как промах.
Задание.
На основании данных об изменении индекса цен на первичном рынке жилья по Российской Федерации, приведенных в таблице, проверить наличие аномальных наблюдений по критерию Ирвина.
| Год | ||||||||

| 156,9 | 146,3 | 113,1 | 125,1 | 122,5 | 118,8 | 118,5 | 117,5 |
| Год | ||||||||

| 147,7 | 123,4 | 110,3 | 92,4 | 100,3 | 106,7 | 110,7 |
Таблица 7. Статистические критерии на наличие грубой погрешности
 грубой погрешности (промаха) нет грубой погрешности (промаха) нет
 грубая погрешность (промах) есть грубая погрешность (промах) есть
| ||
| Критерии | ||
n  10 10
| n  20 20
| n>20…50 |
| Диксона | Романовского | Трех сигм |
Условие отклонения гипотезы 
| ||
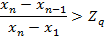
| 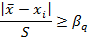
|

|
| - | *при расчете 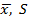 сомнительное значение исключено сомнительное значение исключено
| |
| Критерии | ||
n  10 10
| n<50 | n>20…50 |
| Шовине | Граббса | Ирвина |
Условие отклонения гипотезы 
| ||
n=3:  n=6:
n=6:  n=8:
n=8:  n=10:
n=10: 
|

|

|
*при расчете  сомнительное значение учитывается сомнительное значение учитывается
|