Лекция 1. (С 1-7 стр теория)
основные понятия анализа статистических данных. Простая регрессия.
Эконометрические методы – это, прежде всего, методы статистического анализа конкретных экономических данных.
Структура методов.
В как дисциплине на стыке экономики (включая менеджмент) и статистического анализа, естественно выделить три направления научной и прикладной деятельности:
1). Разработка и исследование эконометрических методов с учетом специфики экономических данных
2). Разработка и исследование эконометрических моделей в соответствии с конкретными потребностями экономической науки и практики
3). Применение эконометрических методов и моделей для статистического анализа конкретных экономических данных
Основная задача: на основании экспериментальных данных определить объясняющую часть и случайную компоненту некоторого зависимого фактора. Т.е. составить математическую модель вида
 , где
, где
у – фактические значения зависимого фактора
ух – теоретические значения зависимого фактора (объясняющая часть)
е – случайная компонента
Уравнение вида  называют уравнение регрессии.
называют уравнение регрессии.
Различают регрессии простую (парную) и множественную. Уравнение простой регрессии имеет вид

Уравнение множественной регрессии имеет вид

Основная цель: построить модель, хорошо определяющую состояние реальной экономической ситуации. Основная цель достигается методами эконометрического моделирования.
Можно выделить шесть основных этапов моделирования: постановочный, априорный, этап параметризации, информационный, этапы идентификации и верификации модели.
Остановимся на каждом этапе и рассмотрим проблемы, связанные с их реализацией.
Этап - постановочный.
Формируется цель исследования, набор участвующих в модели экономических переменных.
В качестве цели моделирования обычно рассматривают анализ исследуемого экономического объекта (процесса); прогноз его экономических показателей, имитацию развития объекта при различных значениях экзогенных переменных (экзогенные переменные – задаваемые извне переменные), выработку управленческих решений.
При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при это рекомендуется, чтобы их число было не очень большим, и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной зависимостью или тесной корреляционной, так как это может привести к невозможности оценки параметров модели или получению неустойчивых, не имеющих реального смысла оценок.
2) этап – априорный. Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации.
3) этап – параметризация. Осуществляется непосредственное моделирование, т.е. выбор общего вила модели, выявление входящих в нее связей.
Основная задача, решаемая на этом этапе – выбор вида функции  в эконометрической модели, в частности, возможность использования линейной модели как наиболее простой и надежной. Весьма важной проблемой на этом этапе эконометрического моделирования является проблема спецификации модели, в частности: выражение в математической форме обнаруженных связей и соотношений; установление состава экзогенных и эндогенных переменных (эндогенные переменные – переменные формирующие внутри функционирование объекта); формулировка исходных предпосылок и ограничений модели.
в эконометрической модели, в частности, возможность использования линейной модели как наиболее простой и надежной. Весьма важной проблемой на этом этапе эконометрического моделирования является проблема спецификации модели, в частности: выражение в математической форме обнаруженных связей и соотношений; установление состава экзогенных и эндогенных переменных (эндогенные переменные – переменные формирующие внутри функционирование объекта); формулировка исходных предпосылок и ограничений модели.
4) этап – информационный. Осуществляется сбор необходимой статистической информации – наблюдаемых значений экономических переменных.
5) этап – идентификация модели. Осуществляется статистический анализ модели и оценка параметров.
6) этап – верификация модели. Производится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации модели, какова точность расчетов по данной модели, насколько соответствует построенная модель реальному экономическому объекту.
При постановке задач эконометрического моделирования следует определить их иерархический уровень и профиль. Анализируемые задачи могут относиться к макро- (страна, межстрановой анализ), мезо- (регионы внутри страны) и микро- (предприятия, фирмы, семьи) уровням и быть направленными на решение вопросов различного профиля инвестиционной, финансовой или социальной политики, ценообразования, распределительных отношений и т.п.
Простая регрессия.
Итак, уравнение простой регрессии имеет вид:

Различают шесть основных типов парной регрессии:
Таблица. Типы приближений.
| Тип | Описание |
| Линейная | 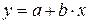 , где , где  - угловой коэффициент, - угловой коэффициент, 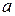 - отрезок на оси ординат - отрезок на оси ординат
|
| Логарифмическая | 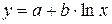 , где , где  - константы - константы
|
| Полиномиальная | 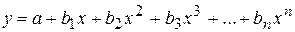 , где , где  - константы - константы
|
| Степенная | 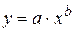 , где , где  - константы - константы
|
| Экспоненциальная |  , где , где  - константы - константы
|
Построение линейной простой регрессии.
Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в СППР ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
 или
или  (1)
(1)
Уравнение вида  позволяет по заданным значениям фактора
позволяет по заданным значениям фактора  находить теоретические значения результативного признака, подставляя в него фактические значения фактора
находить теоретические значения результативного признака, подставляя в него фактические значения фактора  .
.
Построение линейной регрессии сводится к оценке ее параметров 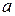 и
и  .
.
Система линейных уравнений для оценки параметров 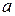 и
и  :
:
 (2)
(2)
Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (2):
 (3)
(3)
 (4)
(4)
Где 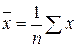 ,
,  ,
,  ,
,  .
.
Параметр  называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально 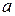 – значение
– значение  при
при  . Если признак-фактор
. Если признак-фактор 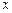 не может иметь нулевого значения, то вышеуказанная трактовка свободного члена
не может иметь нулевого значения, то вышеуказанная трактовка свободного члена  не имеет смысла, т.е. параметр
не имеет смысла, т.е. параметр  может не иметь экономического содержания.
может не иметь экономического содержания.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции  , который можно рассчитать по следующим формулам:
, который можно рассчитать по следующим формулам:
 (5)
(5)
Линейный коэффициент корреляции находится в пределах:  . Чем ближе абсолютное значение
. Чем ближе абсолютное значение  к единице, тем сильнее линейная связь между факторами (при
к единице, тем сильнее линейная связь между факторами (при 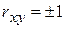 имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции  , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака  , объясняемую регрессией, в общей дисперсии результативного признака.
, объясняемую регрессией, в общей дисперсии результативного признака.
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации (среднюю ошибку приближения):
 (6)
(6)
Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка значимости уравнения регрессии в целом производится на основе  - критерия Фишера, которому предшествует дисперсионный анализ.
- критерия Фишера, которому предшествует дисперсионный анализ.
Величина  - критерия связана с коэффициентом детерминации
- критерия связана с коэффициентом детерминации  , и ее можно рассчитать по следующей формуле:
, и ее можно рассчитать по следующей формуле:
 (7)
(7)
Фактическое значение  - критерия Фишера (7) сравнивается с табличным значением
- критерия Фишера (7) сравнивается с табличным значением 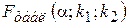 при уровне значимости
при уровне значимости  и степенях свободы
и степенях свободы  и
и  , где
, где  - число параметров уравнения регрессии,
- число параметров уравнения регрессии,  - число данных. При этом, если фактическое значение
- число данных. При этом, если фактическое значение  -критерия больше табличного, то признается статистическая значимость уравнения в целом.
-критерия больше табличного, то признается статистическая значимость уравнения в целом.
Рассмотрим пример нахождения уравнения парной линейной регрессии, а также коэффициентов для оценки качества.
Статистические данные приведены в таблице
Расходы на продукты питания,  , тыс. руб. , тыс. руб.
| Доходы семьи, 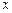 ,тыс. руб. ,тыс. руб.
|
| 0,9 | 1,2 |
| 1,2 | 3,1 |
| 1,8 | 5,3 |
| 2,2 | 7,4 |
| 2,6 | 9,6 |
| 2,9 | 11,8 |
| 3,3 | 14,5 |
| 3,8 | 18,7 |
Предположим, что связь между доходами семьи и расходами на продукты питания линейная. Для иллюстрации предположения построим поле корреляции.

Рис.1. Поле корреляции
По графику видно, что точки выстраиваются в некоторую прямую линию.
Для удобства дальнейших вычислений составим таблицу.
Таблица 1.
На первом этапе заполняем ячейки, выделенные цветом.

| 
| 
| 
| 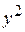
| 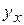
| 
|  , % , %
| |
| 1,2 | 0,9 | 1,08 | 1,44 | 0,81 | 1,038 | 0,0190 | 15,33 | |
| 3,1 | 1,2 | 3,72 | 9,61 | 1,44 | 1,357 | 0,0246 | 13,08 | |
| 5,3 | 1,8 | 9,54 | 28,09 | 3,24 | 1,726 | 0,0055 | 4,11 | |
| 7,4 | 2,2 | 16,28 | 54,76 | 4,84 | 2,079 | 0,0146 | 5,50 | |
| 9,6 | 2,6 | 24,96 | 92,16 | 6,76 | 2,449 | 0,0228 | 5,81 | |
| 11,8 | 2,9 | 34,22 | 139,24 | 8,41 | 2,818 | 0,0067 | 2,83 | |
| 14,5 | 3,3 | 47,85 | 210,25 | 10,89 | 3,272 | 0,0008 | 0,85 | |
| 18,7 | 3,8 | 71,06 | 349,69 | 14,44 | 3,978 | 0,0317 | 4,68 | |
| Итого | 71,6 | 18,7 | 208,71 | 885,24 | 50,83 | 18,717 | 0,1257 | 52,19 |
| Среднее значение | 8,95 | 2,34 | 26,09 | 110,66 | 6,35 | 2,34 | 0,0157 | 6,52 |
Рассчитаем параметры линейного уравнения парной регрессии  . Для этого воспользуемся формулами (3),(4):
. Для этого воспользуемся формулами (3),(4):

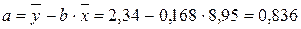 .
.
Получили уравнение:  . Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб.
. Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб.
Как было указано выше, уравнение линейной регрессии всегда дополняется показателем тесноты связи – линейным коэффициентом корреляции  :
:
 .
.
Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками.
Коэффициент детерминации  показывает, что уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,3%.
показывает, что уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,3%.
Оценим качество уравнения регрессии в целом с помощью  - критерия Фишера. Фактическое значение
- критерия Фишера. Фактическое значение  - критерия:
- критерия:
 .
.
Табличное значение  . Так как
. Так как  , то признается статистическая значимость уравнения в целом.
, то признается статистическая значимость уравнения в целом.
Средняя ошибка аппроксимации (находим с помощью столбца 10 таблицы 1);

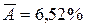 говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.
говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.