Организационный момент
Учитель: Здравствуйте, ребята! Дежурный, кто отсутствует на уроке?
Учитель: Запишите число, классная работа и тему урока. Сегодня на уроке мы закрепим тему «Сложение и умножение числовых неравенств». Вы узнаете, как выполняется сложение и умножение числовых неравенств.
Актуализация опорных знаний
Учитель: Вспомним определение числового неравенства.
Ученик: Число 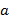 больше числа
больше числа 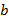 , если разность
, если разность 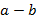 - положительное число; число
- положительное число; число 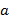 меньше числа
меньше числа 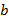 , если разность
, если разность 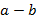 - отрицательное число.
- отрицательное число.
Учитель: Сформулируйте теоремы, выражающие основные свойства числовых неравенств. Для каждого свойства приведите примеры.
Ученик: Теорема 1. Если 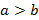 , то
, то 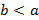 ; если
; если 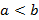 , то
, то 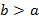 .
.
Пример: Если 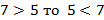 ; если
; если 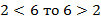 .
.
Ученик: Теорема 2. Если 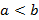 и
и 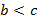 , то
, то 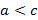 .
.
Пример: Если 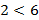 и 6
и 6 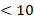 , то 2
, то 2 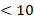 .
.
Ученик: Теорема 3. Если 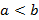 и
и 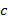 - любое число, то
- любое число, то  .
.
Пример: Если 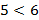 и
и 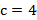 , то
, то 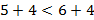 ,
, 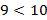 .
.
Ученик: Теорема 4. Если 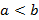 и
и 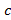 – положительное число, то
– положительное число, то 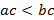 . Если
. Если 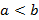 и
и 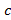 – отрицательное число, то
– отрицательное число, то 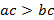 .
.
Если обе части верного неравенства умножить или разделить а одно и то же положительное число, то получится верное неравенство; если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
Пример: 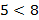 и
и 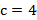 , то
, то 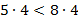 ,
, 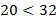 .
.
Пример: 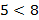 и
и 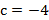 , то
, то 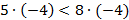 ,
, 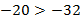 .
.
Ученик: Следствие. Если 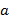 и
и 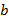 - положительные числа и
- положительные числа и 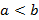 , то
, то 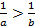 .
.
Пример: 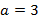 ,
, 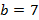 и
и 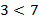 , то
, то 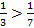 .
.
Изучение нового материала.
Учитель: Если почленно сложить верные неравенства одного знака, то получится верное неравенство. Записываем, теорема 5. Если 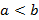 и
и 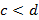 , то
, то 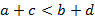 .
.
Пример,  и 3
и 3 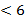 ,
, 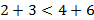 ,
, 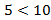 .
.
Запись в тетрадях: Теорема 5. Если 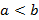 и
и 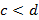 , то
, то 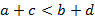 .
.
Пример,  и 3
и 3 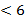 ,
, 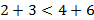 ,
, 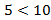 .
.
Учитель: Докажем теорему. Что нам дано?
Ученик: Нам даны два числовых неравенства 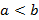 и
и 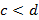 .
.
Учитель: А что нам нужно доказать?
Ученик: Что 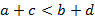 .
.
Учитель: Как думаете, на что мы будем опираться при доказательстве данной теоремы?
Ученик: На свойства числовых неравенств.
Учитель: Док-во. Давайте прибавим к обеим частям неравенства 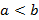 число
число 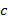 . Что мы получим?
. Что мы получим?
Ученик: Для этого мы воспользуемся теоремой 3, которая выражает одно из свойств числовых неравенств. У нас получится  .
.
Учитель: Теперь давайте прибавим к обеим частям неравенства 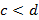 число
число 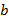
Ученик: Мы так же воспользуемся теоремой 3, и у нас получится 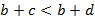 .
.
Учитель: И какой мы вывод можем сделать?
Ученик: Если  и
и 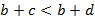 , то
, то 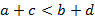 .
.
Учитель: Что нам и требовалось доказать. Теорема доказана.
Учитель: Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство. Записываем, теорема 6. Если 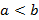 и
и 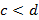 , где
, где 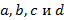 - положительные числа, то
- положительные числа, то 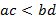 .
.
Пример,  и 3
и 3 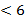 ,
, 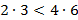 ,
, 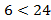 .
.
Запись в тетрадях: Теорема 6. Если 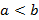 и
и 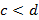 , где
, где 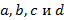 - положительные числа, то
- положительные числа, то 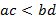 . Пример,
. Пример,  и 3
и 3 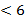 ,
, 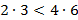 ,
, 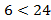 .
.
Учитель: Докажем теорему. Что нам дано?
Ученик: Нам даны два числовых неравенства 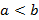 и
и 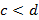 , где
, где 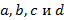 - положительные числа.
- положительные числа.
Учитель: А что нам нужно доказать?
Ученик: Что 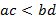 .
.
Учитель: Док-во. Давайте умножим обе части неравенства 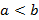 на положительное число
на положительное число 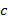 . Что мы получим?
. Что мы получим?
Ученик: Для этого мы воспользуемся теоремой 4, которая выражает одно из свойств числовых неравенств. У нас получится 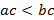 .
.
Учитель: Теперь давайте умножим обе части неравенства 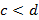 на положительное число
на положительное число 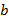 .
.
Ученик: Мы так же воспользуемся теоремой 4, и у нас получится 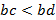 .
.
Учитель: И какой мы вывод можем сделать?
Ученик: Если 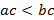 и
и 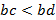 , то
, то 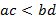 .
.
Учитель: Что нам и требовалось доказать. Теорема доказана.
Учитель: Теперь запишем следующее. Следствие. Если числа 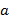 и
и 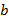 положительны и
положительны и 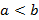 , то
, то  , где
, где 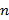 - натуральное число.
- натуральное число.
Пример,  ,
,  ;
; 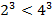 ,
, 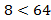 .
.
Запись в тетрадях: Следствие. Если числа 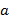 и
и 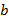 положительны и
положительны и 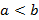 , то
, то  , где
, где 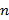 - натуральное число.
- натуральное число.
Пример,  ,
,  ;
; 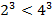 ,
, 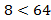 .
.
Учитель: Доказанные свойства используются для оценки суммы, разности, произведения и частного. Разберем пример из учебника на странице 162.
Пусть, например, известно, что 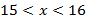 и
и 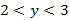 . Требуется оценить сумму
. Требуется оценить сумму 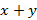 , разность
, разность 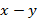 , произведение
, произведение 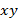 и частное
и частное  .
.
1. Оценим сумму 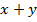 .
.
Применив теорему о почленном сложении неравенств к неравенствам 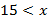 и
и 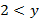 , а затем к неравенствам
, а затем к неравенствам 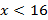 и
и  , получим
, получим 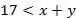 и
и 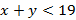 . Результат можно записать в виде двойного неравенства
. Результат можно записать в виде двойного неравенства 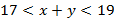 . Запись обычно ведут короче:
. Запись обычно ведут короче:
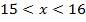
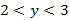
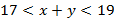
2.  Оценим разность
Оценим разность 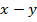 .
.
Для этого представим разность 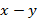 в виде суммы
в виде суммы  . Сначала оценим выражение
. Сначала оценим выражение 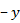 . Так как
. Так как 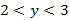 , то
, то 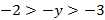 , т. е.
, т. е. 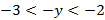 . Применим теперь теорему о почленном сложении неравенств:
. Применим теперь теорему о почленном сложении неравенств:
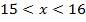

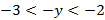

3. Оценим произведение 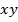 .
.
Так как каждое из чисел 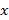 и
и  заключено между положительными числами, то они так же являются положительными числами. Применив теорему о почленном умножении неравенств, получим
заключено между положительными числами, то они так же являются положительными числами. Применив теорему о почленном умножении неравенств, получим
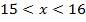
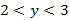
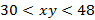
4.  Оценим частное
Оценим частное  .
.
Для этого представим частное  в виде произведения
в виде произведения  . Сначала оценим выражение
. Сначала оценим выражение  . Так как
. Так как 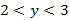 , то
, то 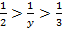 , т. е.
, т. е. 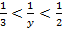 . По теореме о почленном умножении неравенств имеем
. По теореме о почленном умножении неравенств имеем

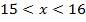
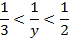
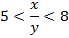
4. Формирование умений и навыков.
Учитель: Теперь решаем номер 765.
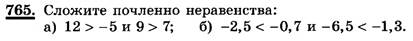
Ученик: № 765.
а)  и
и 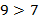 , то по теореме 5 получаем
, то по теореме 5 получаем 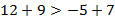 ,
, 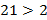
б) 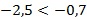 и
и 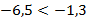 , то по теореме 5 получаем
, то по теореме 5 получаем 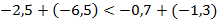 ,
, 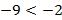
Запись на доске и в тетрадях:
№ 765.
а)  и
и 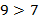 , то по теореме 5 получаем
, то по теореме 5 получаем 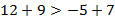 ,
, 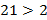
б) 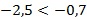 и
и 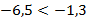 , то по теореме 5 получаем
, то по теореме 5 получаем 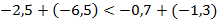 ,
, 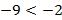
Учитель: Теперь выполняем номер 766.

Ученик: № 766.
а)  и
и 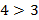 , то по теореме 6 получаем
, то по теореме 6 получаем 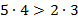 ,
, 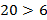
б) 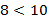 и
и 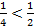 , то по теореме 6 получаем
, то по теореме 6 получаем 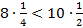 ,
, 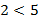
Запись на доске и в тетрадях:
№ 766.
а)  и
и 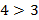 , то по теореме 6 получаем
, то по теореме 6 получаем 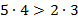 ,
, 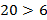
б) 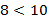 и
и 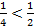 , то по теореме 6 получаем
, то по теореме 6 получаем 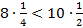 ,
, 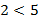
Учитель: Решаем № 768.
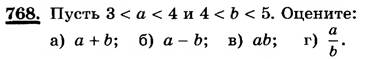
Ученик: № 768.
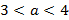 и
и 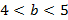 .
.
а) 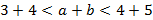 ;
;  .
.
б) Сначала оценим выражение 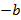
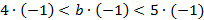 ;
; 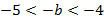 .
.
 ;
; 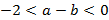 .
.
в) 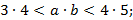
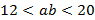 .
.
г) Сначала оценим выражение 
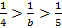 , т.е.
, т.е. 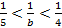
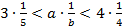 ,
, 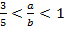
Запись на доске и в тетрадях:
№ 768.
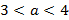 и
и 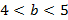 .
.
а) 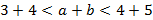 ;
;  .
.
б) Сначала оценим выражение 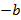
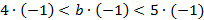 ;
; 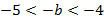 .
.
 ;
; 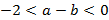 .
.
в) 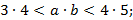
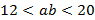 .
.
г) Сначала оценим выражение 
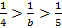 , т.е.
, т.е. 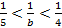
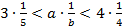 ,
, 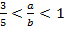
Учитель: Теперь № 770.
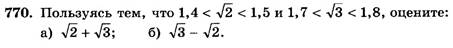
Ученик: № 770.
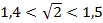 и
и 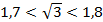
а) 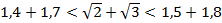 ;
;  .
.
б) 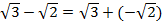 ;
; 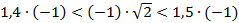 ;
;
 ;
; 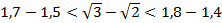 ;
; 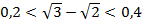 .
.
Запись на доске и в тетрадях:
№ 770.
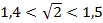 и
и 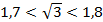
а) 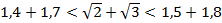 ;
;  .
.
б) 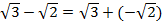 ;
; 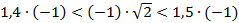 ;
;
 ;
; 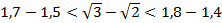 ;
; 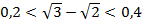 .
.
Учитель: № 772.

Ученик: № 772. Периметр равнобедренного треугольника равен  . Нам даны два двойных неравенства
. Нам даны два двойных неравенства 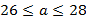 и
и 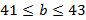 . Но нам не известно
. Но нам не известно  , найдем его
, найдем его 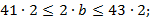
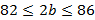 . Теперь мы можем оценить и сам периметр
. Теперь мы можем оценить и сам периметр
 ;
; 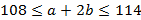 ,
, 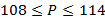
Запись на доске и в тетрадях:
№ 772.
 ;
; 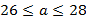 и
и 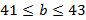
1) 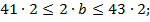
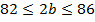 .
.
2) 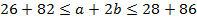 ;
; 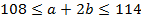 ,
, 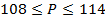
Учитель: № 774.
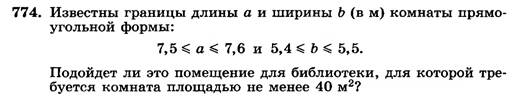
Ученик: № 774.
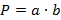 - так как комната прямоугольной формы;
- так как комната прямоугольной формы;
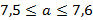 и
и 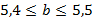
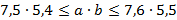 ;
; 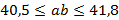 , значит, помещение подойдет для библиотеки.
, значит, помещение подойдет для библиотеки.
Запись на доске и в тетрадях:
№ 774.
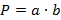 - так как комната прямоугольной формы;
- так как комната прямоугольной формы;
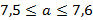 и
и 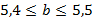
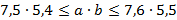 ;
; 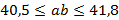 , значит, помещение подойдет для библиотеки.
, значит, помещение подойдет для библиотеки.
Подведение итогов
Учитель: Подведем итоги. Мы сегодня с вами изучили теоремы сложения и умножения числовых неравенств. Сформулируйте теорему 5.
Ученик: Если почленно сложить верные неравенства одного знака, то получится верное неравенство. Если 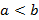 и
и 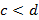 , то
, то 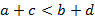 .
.
Учитель: Теперь сформулируйте теорему 6.
Ученик: Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство. Если 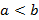 и
и 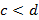 , где
, где 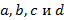 - положительные числа, то
- положительные числа, то 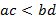 .
.
Учитель: Сформулируйте следствие из теоремы 6.
Ученик: Если числа 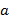 и
и 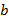 положительны и
положительны и 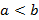 , то
, то  , где
, где 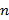 - натуральное число.
- натуральное число.
Учитель: Спасибо за урок, Урок окончен, можете идти.
Учитель выставляет отметки учащимся, кто отвечал на уроке и работал у доски.
Домашнее задание
№ 781