Введение
В данной работе будут рассмотрены следующие вопросы:
1) «Классификация дифференциальных уравнений в частных производных второго порядка»
2) «Уравнение теплопроводности в задаче о неравномерном и нестационарном нагреве стержня»
3) «МКЭ для уравнения Пуассона»
По всем трем рассматриваемым вопросам будут изложены примеры применения.
1. Классификация дифференциальных уравнений в частных производных второго порядка.
В математической физике при рассмотрении задач, связанных с решением уравнений в частных производных второго порядка, всегда концентрируются на анализе некоторых основных уравнений: Пуассона, теплопроводности, волнового уравнения. Связано это с возможностью приведения уравнений второго порядка к т.н. каноническому виду, а именно к тем самым перечисленным только что уравнениям.
Рассмотрим уравнение второго порядка общего вида (уравнение №1):
уравнение№1:
где 
. При этом будем считать без ограничения общности, что матрица коэффициентов симметрическая, т.е. 
(это фактически требование независимости смешанных производных от порядка дифференцирования). Далее будем называть эту матрицу матрицей старшихкоэффициентов.
Строго говоря, одно и то же уравнение в различных точках может относиться к разным типам классификации. Пример будет приведён позже.
В связи с этим замечанием будем говорить о матрице старших коэффициентов в определённой точке. Считаем, что матрица старших коэффициентов представляетсобой матрицу некоторой квадратичной формы. Эту форму можно привести к нормальному виду, т.е. диагональному виду с коэффициентами, равными по модулюнулю или единице. Напомним, что число положительных коэффициентов называется положительным индексом инерции квадратичной формы, число отрицательных коэффициентов – отрицательным индексом формы, а число нулевых коэффициентов – дефектом формы. Уравнения можно классифицировать при помощи этих трёх чисел, которые и будем указывать в порядке их перечисления:.Сумма этих трёх чисел равна количеству независимых переменных.
При этом ясно, что умножение всего уравнения на минус единицу приведёт к тому, что все элементы матрицы старших коэффициентов поменяют знак. Следовательно, положительный и отрицательный индексы соответствующей формы поменяются ролями. Таким образом, уравнения и принадлежат к одному типу классификации.
Перечислим основные классы уравнений:
- гиперболическое
- параболическое
- эллиптическое
- ультрагиперболическое
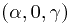- эллиптико-параболическое
Последние два типа уравнений в стандартных курсах не обсуждаются.
Словесно эту классификацию можно сформулировать следующим образом. Уравнение гиперболическое, если дефект соответствующей квадратичной формы равен нулю, а один из индексов равен единице. Уравнение параболическое, если его форма имеет равный единице дефект и все коэффициенты одного знака.
Уравнение эллиптическое, если дефект его формы равен нулю и все коэффициенты имеют одинаковый знак.
1.1 Примеры приведения уравнений второго порядка к каноническому виду
1.1.1 Пример 1. Случай линейной замены переменных в уравнении гиперболического типа:
Составляем характеристическое уравнение:
.
Исходное уравнение, таким образом, относится к гиперболическому типу. Находим общие интегралы найденных уравнений:
.
Вводим замену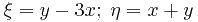 
. Преобразуем производные. В данном случае можно считать, что функция 
зависит от переменных 
,
которые в свою очередь зависят от старых переменных 
:
.
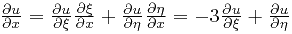
После подстановки этих производных в исходное уравнение получим
.
Пример 2. Случай линейной замены переменных в уравнении эллиптического типа.
Составляем характеристическое уравнение:
.
Исходное уравнение, таким образом, относится к эллиптическому типу. Находим общий интеграл любого из найденных уравнений:
.
Вводим замену 
. Преобразуем производные совершенно аналогично тому, как это делалось в примере 1.
После подстановки этих производных в исходное уравнение получим
.
Большая часть всех уравнений в частных производных 2го порядка, линейных относительно вторых производных являются представителями 3х различных классов уравнений, которые существенно отличаются друг от друга по методам исследования и по физической природе (описывают различные физические явления).
Остановимся более подробно на случае 2х независимых переменных: u = u (x,y).
a,b,c - функции, определенные в некоторой области Ω = Oxy и имеющие непрерывные производные до 2го порядка.
f - непрерывная функция своих аргументов; если f - линейная относительно u, ux, uy, то уравнение (1) - линейное.Поставим перед собой задачу: с помощью замены независимых переменных (x, y) привести уравнение (1) к наиболее простому виду.
Введем новые переменные: 
, и потребуем, чтобы они были дважды непрерывно-дифференцируемы и чтобы якобиан перехода:
в области Ω.
Преобразуем производные к новым переменным:
Тогда уравнение (1) в новых переменных примет вид:
где
Попытаемся выбрать ξ (x, y) и η (x, y) так, чтобы обратить в нуль некоторые из коэффициентов A,B,C.
Вопрос об обращении A и С в нуль эквивалентен вопросу о разрешимости дифференциального уравнения 1го порядка.
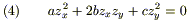относительно неизвестной функции z (x, y).
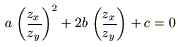Поделим на zy2:
Решим как квадратное уравнение относительно 
:
Решая каждое из них методом характеристик:
- интегралы системы (*), а, следовательно, решения уравнения (4).
Уравнения (5) могут быть записаны в виде одного уравнения:
Обычно это уравнение и используют для определения интегралов системы (5). Поведение функций φ (x, y) и ψ (x, y), а, следовательно, и искомый простейший вид исходного уравнения зависит от знака 
Уравнение теплопроводности в задаче о неравномерном и нестационарном нагреве стержня
Предложен единый алгоритм решения одномерных нестационарных задач теплопроводности в телах простой геометрической формы с внутренними источниками энергии различной природы.
Рассматриваемые тела могут иметь форму пластины, стержня (ребра), сплошного или полого цилиндров и шара. В основе решения поставленной задачи лежат обобщенная формулировка неоднородного дифференциального уравнения нестационарной теплопроводности в частных производных для тел указанной формы и метод интегральных преобразований в конечных пределах.
Процедура решения конкретной краевой задачи предусматривает наличие математической модели, но не требует интегрирования дифференциального уравнения теплопроводности.
Приведен пример определения температурного поля в пластине с неравномерно распределенными источниками теплоты и разными условиями теплообмена на граничных поверхностях.
Решения задач рассматриваемого типа удобно, в частности, использовать для тестирования сложных программ расчета температурного поля теплонагруженных элементов конструкции, анализа их теплового режима на начальной стадии проектирования и обоснования выбираемых допущений.
2.1 Уравнение теплопроводности в стержне.
Рассмотрим тонкий изолированный (покрытый тепловой изоляцией) стержень, лежащий на отрезке 
оси 
(рис. 124). Предполагается, что его физические свойства в точках любого его сечения одинаковы. Температура стержня есть функция
от абсциссы сечения и времени 
.
Функция 
удовлетворяет дифференциальному уравнению в частных производных, рассмотрим уравнение 1.
Уравнение 1:
, где 
- константа, если предположить, что теплоемкость и теплопроводность стержня не зависят от .
Поставим задачу: найти функцию 
, непрерывную для 
, имеющую непрерывные частные производные 
и 
для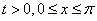 
, удовлетворяющую дифференциальному уравнению 1 для 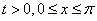, и следующим условиям:
Уравнение 2
, (2)
где 
- заданная на отрезке непрерывная функция;
Уравнение 3
. (3)
Таким образом, предполагается, что в начальный момент времени 
температура в стержне выражается функцией , а на протяжении всего времени опыта на концах стержня искусственно поддерживается температура нуль.
Уравнение 1 будем решать методом Фурье разделения переменных. Суть его заключается в том, что мы отыскиваем частные решения уравнения (1), удовлетворяющие пока только краевым условиям (3), в виде произведения двух функций, каждая из которых зависит только от одного переменного:
Уравнение 4:
. (4)
При этом мы ищем нетривиальные решения, т. е. тождественно не равные нулю. Из (4) имеем:
.
Подставляя эти выражения в Уравнение 1, получаем
. (5)
В (5) левая часть не зависит от , а правая – от , поэтому
, (6)
где 
- некоторая постоянная.
Таким образом, функция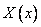 
и 
удовлетворяют обыкновенным дифференциальным уравнениям
, (7)
, (8)
где - некоторая постоянная.
Так как мы ищем решения, удовлетворяющие условиям (3), то при всех должны выполняться равенства
.
Если предположить, что 
, то 
для всех и . Поэтому имеется хотя бы одно , для которого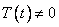 
. Но тогда
. (9)
Мы пришли к следующей задаче. Требуется найти такие числа , для которых дифференциальное уравнение (7) имеет нетривиальное (не равное тождественно нулю) решение на отрезке 
, удовлетворяющее граничным условиям (9).
Задача эта называется проблемой Штурма-Лиувилля для уравнения (7) на отрезке при граничных условиях (9). Искомые числа называются собственными значениями задачи Штурма-Лиувилля, а соответствующие нетривиальные функция, удовлетворяющие граничным условиям (9), называются собственными функциями, соответствующими этим значениям.
Будем искать решение поставленной задачи среди положительных чисел 
. В этом случае числа 
являются корнями характеристического уравнения, поэтому общее решение уравнения (7) запишется так:
.
Из (9) находим
или 
Чтобы получить решение, тождественно не равное нулю, нужно считать 
и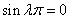 
. Последнее возможно только при натуральных 
.Каждому 
соответствует решение
,
удовлетворяющее, очевидно, граничным условиям (9). Это нетривиальное (тождественно не равное нулю) решение уравнения (7). Итак, числа
суть собственные значения поставленной выше краевой задачи (проблемы Штурма-Лиувидля), а функции
при любом 
- соответствующие этим значениям собственные функции.
Мы нашли все собственные значения и собственные функции поставленной задачи Штурма-Лиувилля, потому что при любом 
дифференциальное уравнение (7) имеет только тривиальное (тождественно равное нулю) решение, удовлетворяющее условиям .