Усилительное (пропорциональное) звено
y (t)= k п x (t)
Переход к передаточной функции:
Y (p)= k п X (p)
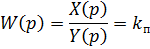
Импульсная характеристика:
k (t)= k пδ(t) = L -1{ W (p)}.
Переходная характеристика:
h (t)= k п1(t) = L -1{ 
W (p)}.
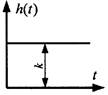
Рис 6.1 – Переходная характеристика усилительного звена
АФХ:
.
,
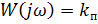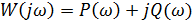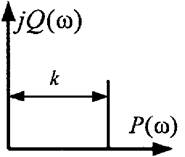
Рис.6.2 АФХ
АЧХ:
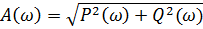
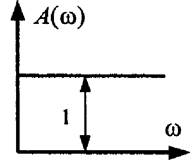
Рис.6.3 АЧХ
ФЧХ:
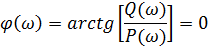
Рис.6.4 ФЧХ
ЛАЧХ:
L (ω)=20 lg k п
Интегрирующее звено
ДУ: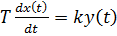 
ПФ: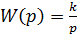 
Примеры.
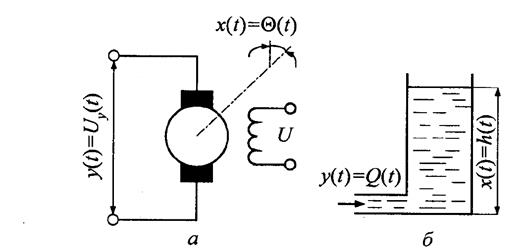
Рис. 6.5. Примеры интегрирующих звеньев: а- электродвигатель постоянного тока; б- резервуар с входным трубопроводом
ИХ: k(t)=k 1(t)
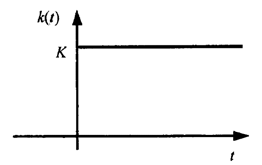
Рис. 6.6. Импульсная характеристика интегрирующего звена
ПХ: h(t)=k t
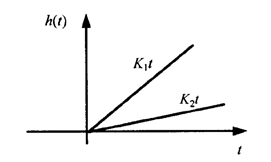
Рис. 6.7. Переходная характеристика интегрирующего звена
Построим частотные характеристики, имеем передаточную функцию:
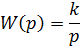
Отсюда
,
где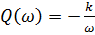 
; P (ω)=0.
АФХ:
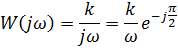
При изменении частоты ω от 0 до ∞ конец вектора W (jω) движется по отрицательной части мнимой оси от -∞ до 0.
Рис. 6.8. АФХ интегрирующего звена
Интегрирующее звено создает отставание гармонического сигнала на 900 на всех частотах ω (рис.6.9).
ФЧХ:
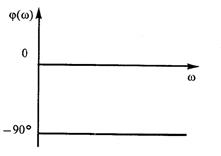
Рис. 6.9. ФЧХ интегрирующего звена
Амплитуда выходного сигнала уменьшается с возрастанием частоты (рис. 6.10).
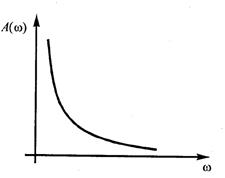
Рис. 6.10. АЧХ интегрирующего звена
Для ЛАЧХ:
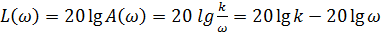(6.1)
В зависимости (6.1) график – прямая линия, поскольку
,
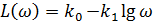так как ось абсцисс –lgω. Построим (1).
Пусть ω = 0, тогда
L(0)=20 lg k – 20lg1=20lg k.
Пусть ω = 10, тогда
L(10)=20 lg k – 20lg10=20lg k-20.
Таким образом, имеем график:
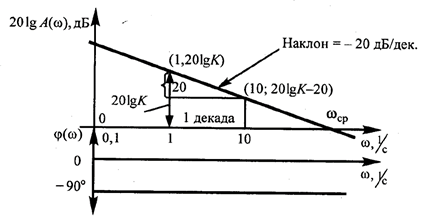
Рис. 6.11. ЛАЧХ и ЛФЧХ интегрирующего звена
Из этого рисунка видно, что при изменении на одну декаду значение ЛАЧХ изменится на -20дБ. Следовательно, она имеет вид прямой.
Апериодическое (инерционное) звено
ДУ имеет вид:
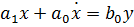
ПФ:
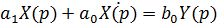
Следовательно:
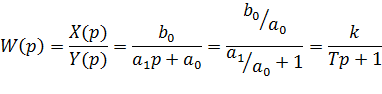
Величины k и T соответственно называются коэффициентом усиления и постоянной времени апериодического звена.
|
|
Примеры апериодических звеньев.
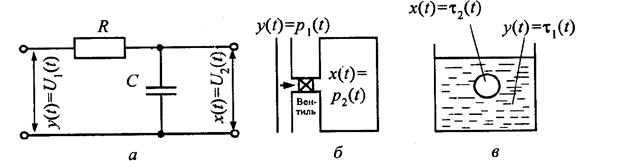
Рис. 6.12. Примеры апериодических звеньев:
а – электрический RC-фильтр; б – резервуар со сжатым газом; в – процесс закалки детали в жидкости
Поскольку
то
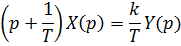
ДУ можно записать в виде:
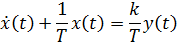
Структурная схема апериодического звена (рис.6.13)
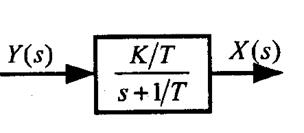
Рис.6.13. Структурная схема апериодического звена
По известным формулам достаточно просто получить зависимости, определяющие импульсную и переходную характеристики:
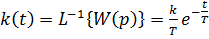, t >0
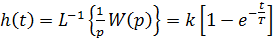, t >0
ИХ и ПХ представлены на рис. 6.14 и 6.15.
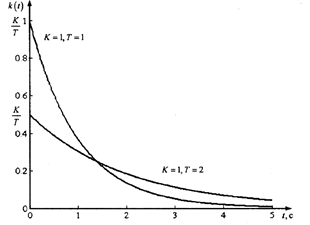
Рис. 6.14. Импульсная характеристика апериодического звена
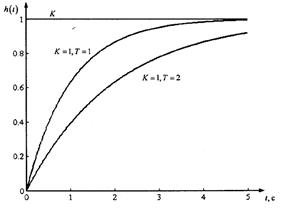
Рис. 6.15. Переходная характеристика апериодического звена
Перепишем переходную характеристику в виде:
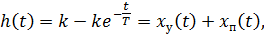
Первая составляющая – это установившейся процесс, второй член обусловлен полюсами ПФ и является собственным движением. Функция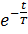 
уменьшается до менее чем 2 % от своего начального значения за 4Т и менее чем 1 % – за 5T. На практике обычно считают, что экспонента уменьшается о нуля за время 4T до 5 T. Таким образом, можно считать, что реакция системы на y(t)=1(t) практически заканчивается через(4..5)T и, следовательно, Т [с] является мерой быстродействия.
Найдем частотные характеристики. Имеем следующую зависимость:
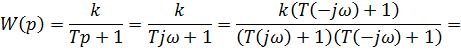
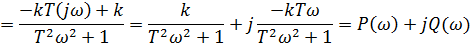
АФХ:
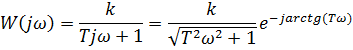
И имеет вид:
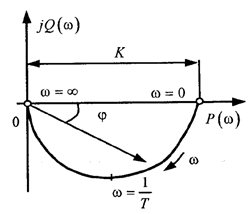
Рис. 6.16. АФХ апериодического звена
Выражение для АЧХ запишется в виде:
ФЧХ:
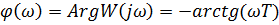
Графики АФХ и ФЧХ представлены на рис.6.17.
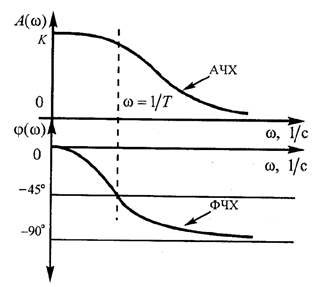
Рис. 6.17. АФХ и ФЧХ апериодического звена
ЛАЧХ определяется формулой
,
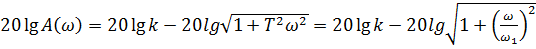где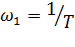 
– частота сопряжения.
Рассмотрим три случая:
1. 
; тогда можно записать
|
|
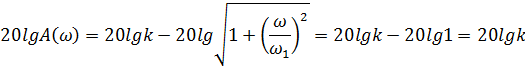
2. 
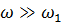; тогда
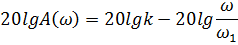
3. Рассмотрим, чему равна L (ω) при ω=ω1 и ω=10 ω1. Пусть ω=ω1, тогда находим
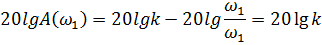
Пусть ω=10ω1, тогда
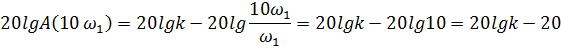
ЛАЧХ представлена на рисунке 6.18
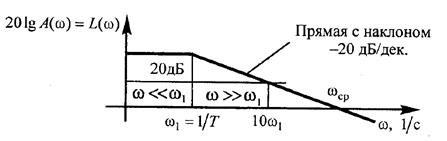
Рис. 6.18 – Приближенная (асимптотическая) ЛАЧХ апериодического звена
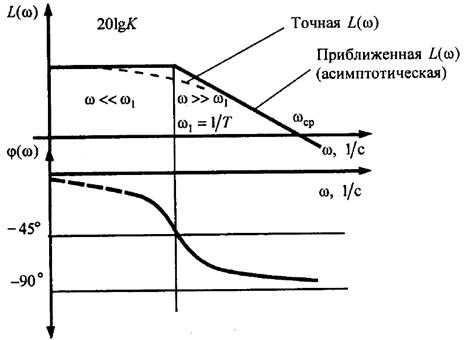
Рис. 6.19 – ЛАЧХ и ЛФЧХ апериодического звена