ПРАКТИКУМ по курсу
Инженерная и компьютерная графика
Содержание
Введение……………………………………………………………………..4
Практическое занятие №1…………………………………………………..4
Практическое занятие №2……………………………………………………5
Практическое занятие № 3……………………………………………………8
Практическое занятие № 4……………………………………………………13
Практическое занятие № 5……………………………………………………22
Практическое занятие № 6…………………………………………………….28
Введение
Практикум составлен в соответствии с программой по начертательной геометрии и стандартом на учебную дисциплину для студентов инженерно-технологических специальностей высших учебных заведений. В практикум включены шесть основных тем.
Каждая тема соответствует модулю карты по курсу.
Практическое занятие №1.
(модуль «Виды проецирования»)
Тема: «Виды проецирования. Комплексный чертеж. Эпюр точки».
Цель занятия: Изучить построение комплексного чертежа на примере чертежа точки.
Продолжительность занятия: 2 часа.
Вопросы для подготовки к занятию.
1. Что изучает начертательная геометрия?
2. Кто является основателем начертательной геометрии?
3. На чем базируются правила изображения в начертательной геометрии?
4. Какой вид проецирования заложен в основу технических чертежей?
Задача
Построить ортогональную проекцию треугольника АВС
А /117; 90; 95/
В /52; 25; 79/
С /0; 83; 48/
Методические рекомендации по выполнению задания.
Для наглядности рассмотрим построение одной точки А.
Чтобы показать изображение предмета, спроецированное на три плоскости проекций, на одной плоскости, мысленно проводят разрез по оси Оу и поворачивают плоскость П1 вокруг оси Ох, а плоскость П3 – вокруг Оz до совмещения с плоскостью П2, получая комплексный чертеж. При этом хА= 117мм; уА=90мм; zА=95мм.
|
|
Отчет по практическому занятию.
Двух проекционный эпюр представляет собой изображения предмета на двух плоскостях проекций, совмещенных с плоскостью чертежа. Им удобно пользоваться, т.к. две любые проекции предмета или точки всегда содержит все три их координаты, однозначно определяющие положение предмета в пространстве. Чертеж является обратимым, поскольку наличие 2-х проекций какого-либо предмета позволяет точно представить его.
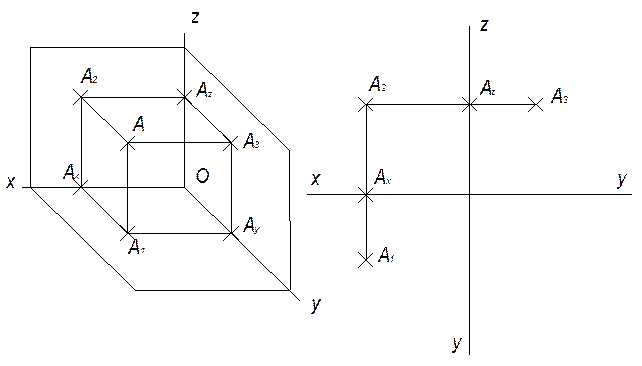
Практическое занятие №2.
Тема: Линии.
Цель занятия: Изучить классификацию прямых по расположению относительно друг друга и расположению относительно плоскостей проекций.
Продолжительностей занятия: 6 часов.
Вопросы для подготовки к занятию.
1. Как могут располагаться прямые в пространстве.
2. Что называется прямой общего положения.
3. Какие прямые частного положения вы знаете?
4. Дать определение фронтали.
5. Что такое профильно-проецирующая прямая.
Задача
В плоскости треугольника АВС через точку А провести горизонталь, а через точку С фронталь.
Методические рекомендации по выполнению задания.
Для построения таких линий используем аксиому, гласящую, что прямая определяется двумя точками. Возьмем точки принадлежащие плоскости, и вспомним, что фронтальная проекция горизонтали и горизонтальная проекция фронтали параллельны оси Х, линии уровня плоскости легко построить.
|
|
Индивидуальное задание №1.
По заданному условию достройте недостающие проекции прямых, определите их положение в пространстве и запишите их наименование.
1) a -?
2) f – величина угла наклона прямой к П1 равна 150º
3) l – на прямой отложите отрезок ЕМ = 20мм
4) 
- на прямой отложите КF= 15мм
5) СД -?
6) h – на прямой отложите отрезок MN= 25мм
7) h – на прямой отложите отрезок LQ=25мм.
Индивидуальное задание №2.
Построение проекций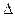 
АВС, если известны:
а) проекции стороны АВ;
б) горизонтальная проекция АС (АС - горизонтальная проекция).
Индивидуальное задание №3.
Достройте фронтальную проекцию плоского четырехугольника АВСД через точку В проведите горизонталь, через точку С - фронталь.
Отчет по практическому заданию
По своему положению в пространстве прямые делятся на прямые общего и частного положения. Прямые частного положения на прямые уровня и проецирующие прямые.
Проецирующие прямые являются и прямыми уровня. Фронтально-проецирующая прямая является и горизонталью и профильной прямой, поскольку она параллельна и горизонтальной и профильной плоскостям проекций. По этой же причине горизонтально-проецирующая прямая и фронталь и профильная прямая, к профильно-проецирующая прямая – горизонталь и фронталь. Следовательно, проецирующие прямые одновременно дважды прямые уровня.