Первичная статистическая обработка данных.
1. Точечный вариационный ряд (ряд 1):
| xi | ni | xi | ni | xi | ni | xi | ni |
| 7 038,00 | 9 408,00 | 11 752,00 | 17 496,25 | ||||
| 7 129,50 | 9 448,00 | 11 789,00 | 17 703,00 | ||||
| 7 413,00 | 9 460,00 | 11 866,25 | 17 803,00 | ||||
| 7 513,00 | 9 465,75 | 12 152,00 | 17 850,00 | ||||
| 7 729,50 | 9 485,75 | 12 327,00 | 18 567,00 | ||||
| 7 938,00 | 9 660,00 | 12 727,00 | 18 758,25 | ||||
| 7 941,00 | 9 712,50 | 12 852,00 | 18 798,25 | ||||
| 8 400,00 | 9 762,50 | 13 110,00 | 18 842,50 | ||||
| 8 400,00 | 9 987,50 | 13 209,00 | 18 952,50 | ||||
| 8 453,00 | 10 027,50 | 13 299,00 | 19 103,00 | ||||
| 8 490,00 | 10 068,00 | 13 995,00 | 19 183,50 | ||||
| 8 536,50 | 10 101,00 | 14 194,50 | 19 483,50 | ||||
| 8 550,50 | 10 140,00 | 14 322,00 | 21 135,00 | ||||
| 8 880,75 | 10 141,00 | 14 794,50 | 21 735,00 | ||||
| 8 898,75 | 10 227,50 | 14 822,00 | 22 050,00 | ||||
| 8 997,00 | 10 668,00 | 15 392,50 | 22 550,00 | ||||
| 9 013,00 | 10 715,00 | 15 592,50 | 23 151,50 | ||||
| 9 057,00 | 10 752,00 | 16 052,25 | 23 551,50 | ||||
| 9 187,50 | 11 040,00 | 16 952,25 | 26 680,00 | ||||
| 9 358,00 | 11 366,25 | 17 456,25 | 26 880,00 |
2. Переходя от ряда 1 к интервальному ряду (ряду 2):
Xmin=7 038,00 руб, Xmax=26 880,00 руб
Вариационный размах: R=Xmax-Xmin= 19 842,00
Разобьем диапазон на k=7 интервалов
Длина каждого интервала h=R/k= 2 834,571
Интервальный ряд (ряд 2)
| xi-xi+1 | ni* |
| 7038,00 - 9872,571 | |
| 9872,531 - 12707,142 | |
| 12707,142 - 15541,713 | |
| 15541,713 - 18376,284 | |
| 18376,284 - 21210,855 | |
| 21210,855 - 24045,426 | |
| 24045,426 – 26880,00 |
Равноточечный ряд (ряд 3)
| xi* | ni* |
| 8455,38 | |
| 11289,86 | |
| 14124,43 | |
| 19793,57 | |
| 25462,7 |
Равноточечный ряд по относительным частотам (ряд 4)
| xi* | wi |
| 8455,38 | 0,35 |
| 11289,86 | 0,2125 |
| 14124,43 | 0,1375 |
| 0,1 | |
| 19793,57 | 0,1125 |
| 0,0625 | |
| 25462,7 | 0,025 |
Построение кумулятивной кривой по ряду 3:
| xi* | mi* |
| 8455,38 | |
| 11289,86 | |
| 14124,43 | |
| 19793,57 | |
| 25462,7 |
3. Построение эмпирической функции распределения по ряду 3:
F*=nx/n, где nx – число элементов выборки (объёма n), меньших, чем x.
| xi* | F* |
| 8455,38 | 0,35 |
| 11289,86 | 0,5625 |
| 14124,43 | 0,7 |
| 0,8 | |
| 19793,57 | 0,9125 |
| 0,975 | |
| 25462,7 |
4. Числовые характеристики выборки:
1. Выборочное среднее <x> и дисперсия D
<x>= 
=13218,64
D= 
= 24654233,3
- Модой Xmod называют варианту, которая имеет наибольшую частоту в нашем случае
Xmod=8455,38
3. Медианной Xmed называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n=2k+1, то Xmed=Xk+11; при четном n=2k медиана Xmed=(Xk+Xk+1)/2.
В нашем случае: Xmed=11559,125.
4. Асимметрия As=μ3 / σв3 = 0,897703
μ3 =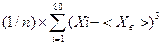 
;
5. Эксцесс Ek = (μ4 / σв4 ) - 3 = -0,10001
μ4 = 
;
5. Оценка близости выборочных наблюдений к нормальному закону:
Асимметрия и эксцесс отличаются от нормального распределения. Эксцесс отрицателен – это значит что кривая имеет более низкую и плоскую вершину, чем нормальная кривая. Асимметрия положительна – кривая имеет правостороннюю скошенность.
Cтатистическое оценивание параметров.
1. Исправленная дисперсия – несмещенная оценка генеральной дисперсии, действительно:
Исправленная дисперсия:
2496641,317
Несмещённая оценка математического ожидания генеральной совокупности:
MX = <xв> = = 13218,64
2. Построение доверительных интервалов для математического ожидания и дисперсии:
Построим доверительные интервалы математического ожидания дисперсии при неизвестных параметрах нормального закона распределения с доверительной вероятностью, равной 0,95 и 0,99. Для математического ожидания воспользуемся следующим выражением для доверительного интервала:
, где 
определится из таблицы по известному значению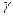 
. Для дисперсии интервал запишется в виде 
, где q находится из таблицы значений.
В нашем случае при доверительной вероятности равной 0,95, =1,001, а q=0,161, тогда интервал для мат. ожидания равен
11739,27323 <MX< 14698,007
при доверительной вероятности равной 0,95, а доверительный интервал дисперсии равен 
А при дов. вероятности равной 0,99 =2,640, а q=0,226, тогда интервал мат. ожидания равен
12752,263 <MX< 17120,267
доверительный интервал дисперсии равен
.
3. Пользуясь компьютерным моделированием получим 50 случайных чисел, лежащих в интервале от 0 до 10. Приведем сразу точечный вариационный ряд:
| Xi | ||||||||||
| ni |
Произведем оценку параметров a и b по методу моментов:
Имеем:
- несмещенные оценки – эмпирические моменты
- находим из курса теории вероятности
Имеем:
; 
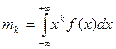Из формул находим:
И
,где 
- поправка Шеттарда.
Найдем 
:
Построим интервальный ряд:
Разобьем диапазон на k=5 интервалов.
Длина каждого интервала - 
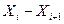
| 0-1,8 | 1,8-3,6 | 3,6-5,4 | 5,4-7,2 | 7,2-9 |
|
Построим равноточечный ряд:
| 0,9 | 2,7 | 4,5 | 6,3 | 8,1 |
|
|
Следовательно, по М.М. имеем оценку параметров a и b: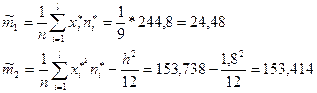 
4. Найти методом максимального правдоподобия точечную оценку неизвестного параметра 
распределения Пуассона, доказать ее несмещенность и состаятельность.
Распределение Пуассона - 
Где m – число произведенных испытаний, 
- число появления события в i-м (i=1,2,...,n) опыте (опыт состоит из m испытаний).
Составим функцию правдоподобия, учитывая что 
:
Найдем логарифмическую функцию правдоподобия:
Найдем первую производную по 
:
Напишем уравнение правдоподобия, для чего приравняем первую производную нулю:
Найдем критическую точку, для чего решим полученное уравнение относительно :
.
Найдем вторую производную по :
.
Легко видеть, что при 
вторая производная отрицательна; следовательно, 
-точка максимума и, значит, в качестве оценки наибольшего правдоподобия параметра распределения Пуассона надо принимать выборочную среднюю 
. Отсюда и следует ее несмещенность и состоятельность.