Математическая логика
Лекция 3
Высказывания
Определение. Высказывание – повествовательное утверждение, которое либо истинно либо ложно (не то и другое одновременно).
Примеры высказываний: "Тише едешь – дальше будешь", "Париж – столица Франции". Но "Как бы чего не вышло" или "Миру – мир" не являются высказываниями.
Определение. Высказывание называется простым (элементарным), если оно рассматривается как одно неделимое целое.
Определение. Сложное высказывание – высказывание, составленное из простых с помощью логических связок.
Логические связки (операции) над высказываниями
Определение. Конъюнкцией ("и") высказываний P и Q называется высказывание, истинное тогда и только тогда, когда оба истинны. Обозначается P & Q.
Таблица истинности:
| P | Q | P & Q |
| л | л | л |
| л | и | л |
| и | л | л |
| и | и | и |
Определение. Дизъюнкцией ("или") высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба ложны. Обозначается 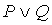 .
.
Таблица истинности:
| P | Q | 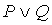
|
| л | л | л |
| л | и | и |
| и | л | и |
| и | и | и |
Определение. Отрицанием ("не") высказывания P называется высказывание, ложное тогда и только тогда, когда P истинно. Обозначается 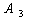 или
или 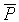 .
.
Таблица истинности:
| P | 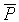
|
| л | и |
| и | л |
Определение. Импликацией высказываний P и Q называется высказывание, ложное, когда P истинно, а Q ложно, и истинное во всех остальных случаях. Обозначается 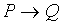 .
.
Таблица истинности:
| P | Q | 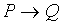
|
| л | л | и |
| л | и | и |
| и | л | л |
| и | и | и |
Определение. Эквивалентностью высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначается 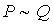 или
или 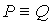 .
.
Таблица истинности:
| P | Q | 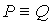
|
| л | л | и |
| л | и | л |
| и | л | л |
| и | и | и |
Определение. Неравнозначностью (сложение по модулю 2) высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q различны, и ложное в противном случае. Обозначается 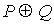 .
.
Таблица истинности:
| P | Q | 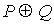
|
| л | л | л |
| л | и | и |
| и | л | и |
| и | и | л |
Пропозициональные формулы
Рассмотрим алфавит 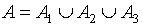 , где
, где 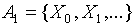 ,
, 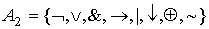 ,
, 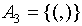 .
.
Символы из 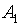 называются переменными высказывания или пропозициональными переменными.
называются переменными высказывания или пропозициональными переменными.
Символы из 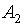 называются логическими связками.
называются логическими связками.
Скобки из 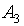 называются вспомогательными символами.
называются вспомогательными символами.
Определение. Пропозициональная формула определяется следующим образом:
1) пропозициональная переменная есть формула;
2) если P и Q – формулы, то Ø P, (P & Q), (PÚ Q),(P® Q),(PÅ Q),(P | Q), (P¯ Q) – формулы,
3) других формул нет.
При этом
а) внешние скобки у формул опускаются;
б) устанавливаются следующие приоритеты:
Ø – выполняется в первую очередь;
& – во вторую очередь;
Ú, ®, Å, |, ¯ – в третью очередь.
Булевы функции. Таблицы истинности
Определение. Булевой функцией 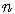 булевых переменных называется функция с областью определения
булевых переменных называется функция с областью определения 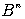 и областью значений
и областью значений 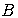 , где
, где 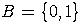 .
.
Способы задания:
1) таблицами истинности; при этом 0 интерпретируется как "ложь", а 1 – как "истина";
2) пропозициональными формулами.
Таблица истинности некоторых логических связок:
| x | y | x & y | xÚ y | Ø x | x® y | XÅ y | x~y |
Булевы функции одной переменной
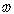
| 
| Обозначение | Наименование |
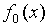
| 
| 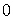
| Константа 0 |
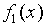
| 
| 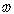
| Тождественная |
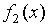
| 
| 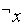
| Отрицание |
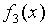
| 
| 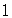
| Константа 1 |