Условные законы распределения
Для дискретных величин были введены условные вероятности по формулам
и 
.
Для непрерывных величин аналогично вводятся плотности для условных законов распределения
и 
.
Числовые характеристики составляющих 
и 
двумерной случайной величины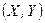 
можно найти по формулам
,
,
,
.
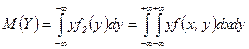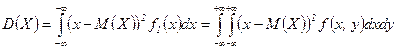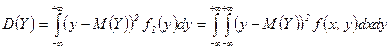Аналогичные характеристики можно ввести и для условных распределений, например, условные математические ожидания
, 
.
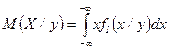Условное математическое ожидание 
будет функцией от 
:
, (1)
и наоборот, условное математическое ожидание 
будет функцией от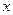 
:
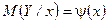. (2)
Функции (1) и (2) называются функциями регрессии: (1) − на , а (2) − на . Графики этих функций называются линиями регрессии или кривыми регрессии.
Зависимые и независимые случайные величины
Определение. Случайные величины и называются независимыми, если условные законы любой из них совпадают с безусловными:
для дискретных случайных величин
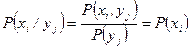, т.е. 
,
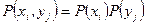для непрерывных
, т.е. 
.
Таким образом, плотность вероятности совместного распределения системы 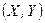равна произведению плотностей распределения составляющих. Это условие является не только необходимым, но и достаточным для непрерывных случайных величин. Точнее, имеет место следующая теорема.
Теорема (критерий независимости случайных величин). Для того, чтобы случайные величины и были независимыми необходимо и достаточно, чтобы функция распределения системы 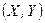была равна произведению функций распределения составляющих:
.
Кроме того, для непрерывных величин это условие равносильно следующему
.
(Доказательство см. в [1].)
Для независимых случайных величин 
, т.е. функция регрессии 
, 
, т.е. функция регрессии 
, а значит, линии регрессии −прямые, параллельные координатным осям.
Пример. Задана плотность вероятности совместного распределения системы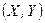
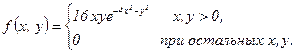
Найдем
.
.
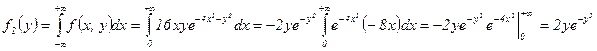Мы видим, что , т.е. случайные величины и являются независимыми.
§ 13. Ковариация (корреляционный момент)
и коэффициент корреляции
Для двумерной случайной величины характеристики ее составляющих и 
, 
, 
, 
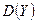никак не отражают зависимости между и или ее отсутствия. Поэтому вводится еще одна числовая характеристика − корреляционный момент или ковариация.
Определение. Ковариацией или корреляционным моментом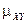 
случайных величин и называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
.
Используя формулы для математических ожиданий, получаем
для дискретных величин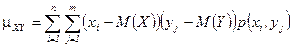 
,
для непрерывных величин 
.
Ковариация характеризует зависимость величин.
Свойства корреляционного момента
1. Для независимых случайных величин и 
.
2. Если 
, то случайные величины и зависимы.
3. 
. (Для доказательства достаточно раскрыть скобки под знаком математического ожидания в определении.) В частности
для дискретных величин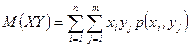 
,
для непрерывных величин 
.
4. 
. (Свойство сразу вытекает из 3.)
5. 
. (Выразите дисперсию через математические ожидания.)
6. 
.
7. 
. (Доказательство этого свойства можно найти в [1, гл.14, § 17].)
Ковариация имеет размерность произведения размерностей случайных величин и и зависит от того, в каких единицах измерялись величины. Для получения безразмерной характеристики вводится понятие коэффициента корреляции.
Определение. Коэффициентом корреляции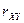 
случайных величин и называется отношение корреляционного момента к произведению средних квадратических отклонений этих случайных величин:
.
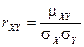Свойства коэффициента корреляции
1. Для независимых случайных величин и 
.
2. 
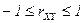. Коэффициент корреляции по абсолютной величине не превосходит единицы.
3. Если 
, то случайные величины и связаны линейной зависимостью, т.е.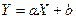 
.
Определение. Случайные величины и называются некоррелированными, если , и коррелированными, если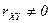 
.
Следует помнить, что понятия некоррелированности и независимости не совпадают, несмотря на внешнее сходство. Независимые величины − некоррелированные, но обратное неверно. Коррелированные величины − зависимые, но обратное неверно. Любые коррелированные величины всегда зависимые, любые независимые величины всегда некоррелированные. Это можно отразить на двудольном графе.
Пример. У случайных величин и 
, 
, 
, 
, 
. Найдите 
и 
.
Решение.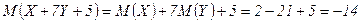 
.
.
Ответ. 
, 
.
В заключение рассмотрим пример на вычисление всех характеристик системы случайных величин.
Пример. Задан закон распределения системы случайных величин :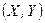
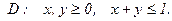
Найдите значение параметра 
. Найдите законы распределения составляющих и . Найдите условные законы распределения составляющих. Найдите , , , , 
, , .
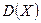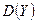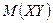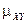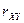Решение. а) Согласно свойству 
совместной плотности вероятности 
системы случайных величин 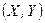(свойство 4 из §10) для заданной плотности также
, т.е. 
. Вычислим интеграл:
. Следовательно, 
.
Итак, плотность вероятности имеет вид
б) Законы распределения составляющих и найдем по формулам:
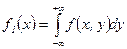− плотность вероятности составляющей и
− плотность вероятности составляющей .
Если 
, то 
, а при 
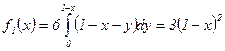, поэтому
Аналогично, если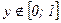 
, то 
, а при 
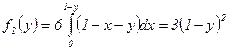, поэтому
в) Условные законы распределения составляющих и найдем по формулам:
и .
при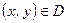 
, т.е.
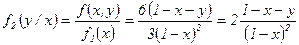при 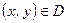, т.е.
г) Математическое ожидание найдем по формуле
, а т.к. отлична от 0 только в области 
, то
.
Аналогично, 
.
Для вычисления дисперсии найдем 
. А т.к. отлична от 0 только в области , то
.
.
Аналогичные вычисления для дают 
.
Средние квадратические отклонения 
и 
.
д) Математическое ожидание 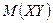найдем по формуле
. А т.к. отлична от 0 только в области , то
.
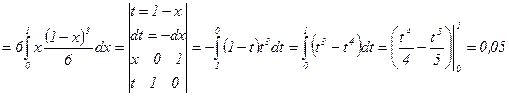е) Корреляционный момент 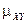найдем по формуле .
.
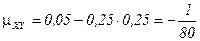Коэффициент корреляции 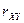вычисляется по формуле .
.
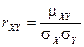Так как коэффициент корреляции отличен от 0, случайные величины и коррелированные, а значит, зависимые.
Ответ. ,
,
, 
, , ,
, 
, 
.
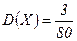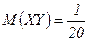Замечание. Симметричные значения для составляющих в данном примере получились благодаря симметричности плотности совместного распределения и области . В общем случае таких совпадений не будет.
Закон больших чисел
В 1913 г. В России был отмечен необычный юбилей − двухсотлетие закона больших чисел. В 1913 г. Была переведена на русский язык «Часть четвертая сочинения Я. Бернулли», опубликованного в 1713 г. через 8 лет после его смерти. Само название «закон больших чисел» принадлежит Пуассону (1781 − 1840).
Что такое «закон больших чисел»?
Под «законом больших чисел» в широком смысле слова понимается общий принцип, согласно которому (по словам А.Н. Колмогорова) совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
В узком (математическом) смысле слова закон больших чисел – это ряд теорем, в которых при тех или иных условиях устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Для каждой случайной величины нельзя предвидеть, какое она примет значение в итоге испытания. Но поведение суммы большого числа случайных величин почти утрачивает случайный характер и становится закономерным, здесь необходимое прокладывает себе дорогу сквозь множество случайностей.
Исторически первой формулировкой больших чисел считается теорема Бернулли, опубликованная в 1713 г. В дальнейшем были получены более простые её доказательства, основанные на неравенстве Чебышева[1].
Теорема Бернулли (современная формулировка).
При неограниченном числе испытаний 
в схеме Бернулли относительная частота (частость) появления события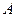 
стремится по вероятности к вероятности 
события :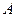
.
Теорема (неравенство Чебышева). Для любого 
и любой случайной величины , имеющей математическое ожидание и дисперсию 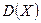, вероятность того, что случайная величина отклонится от 
не меньше чем на 
меньше либо равна 
:
. (1)
Доказательство (для непрерывной случайной величины): ○
. ●
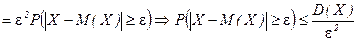− это верхняя граница вероятности, она может быть достаточно большой, существенно больше 1.
Так как события 
и 
противоположные, то другая форма неравенства Чебышева
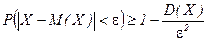. (2)
Здесь дается нижняя оценка вероятности рассматриваемого события.
Пример. Для любой случайной величины по неравенству Чебышева получаем
, в то время как для нормально распределённой величины 
, т. е. оценка по неравенству Чебышева менее точная, но применимая для всех без исключения случайных величин.
Теорема Чебышева. Если 
− попарно независимые случайные величины с равномерно ограниченными дисперсиями, т.е.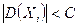 
, то при неограниченном увеличении их среднее арифметическое 
стремится по вероятности к среднему арифметическому их математических ожиданий: 
,
т.е. для любого 
.
Доказательство. ○ По неравенству Чебышева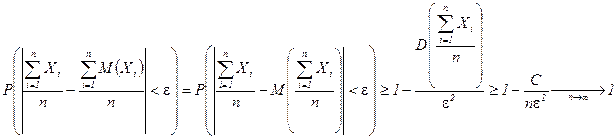 
, т.к. 
. ●
Таким образом, при большом числе случайных величин их среднее арифметическое − случайная величина, сколь угодно мало отличающаяся от постоянной величины 
, т.е. практически перестает быть случайной. В частности, если величины одинаково распределены 
, то 
.
Теорема Чебышева имеет важное практическое значение: при измерении некоторой величины 
, истинное значение которой неизвестно, проводят независимых измерений . Тогда . Этим обосновывается выбор среднего арифметического в качестве меры истинного значения .
Смысл теоремы Чебышева заключается в том, что хотя отдельные независимые величины могут принимать значения, далекие от своих математических ожиданий среднее арифметическое большого числа случайных величин с большой вероятностью принимает значение, близкое к некоторой константе, а именно к . Например, при измерении физической величины проводят несколько независимых измерений и их среднее арифметическое принимают в качестве истинного размера.
К числу теорем закона больших чисел относится и центральная предельная теорема Ляпунова[2]
Теорема (центральная предельная теорема Ляпунова). Распределение суммы попарно независимых случайных величин приближается к нормальному, если:
1. все эти величины имеют конечные математические ожидания и дисперсии
2. ни одна из величин по своим значениям резко не отличается от остальных.
Пример. В университете, куда ежедневно приходят 6400 студентов, имеется 2 входа. Каждый студент с вероятностью 0,5 заходит в любой из них и сдает пальто в соответствующий гардероб. Сколько вешалок должно быть в каждом гардеробе, чтобы с вероятностью, большей 0,997 их хватило?
Решение. С каждым студентом свяжем случайную величину 
, которая примет значение 1, если студент заходит с первого входа и 0 в противном случае. Тогда количество студентов, зашедших с первого входа и сдающих пальто в соответствующий гардероб, равно 
. Законы распределения составляющих, очевидно, таковы
| ||
| 0,5 | 0,5 |
Так как сумма большого числа одинаково распределенных величин по теореме Ляпунова подчиняется нормальному закону распределения, то 
, поэтому достаточно вешалок в промежутке 
, т.е.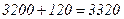 
.
Ответ. 3320 вешалок.
[1] Пафнутий Львович Чебышёв (1821 −1894) − русский математик и механик, его работы по теории вероятностей имели огромное значение для развития математики.
[2] Александр Михайлович Ляпунов (1857 − 1918) − русский математик и механик, выдающийся представитель петербургской математической школы, созданной П.Л. Чебышевым.