В этом случае рассматриваются две нормально распределенные генеральные совокупности 
и 
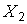с параметрам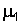и 
, 
и 
, 
соответственно. Из первой совокупности извлекается выборка объема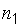 
, из второй – объема 
. Требуется с заданной доверительной вероятностью 
построить доверительный интервал для разности математических ожиданий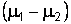 
.
Рассмотрим случай, когда дисперсии 
и 
известны. Тогда случайная величина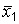 
– среднее арифметическое для выборки из первой генеральной совокупности 
имеет нормальное распределение с параметрами 
. Случайная величина 
среднее арифметическое для выборки из генеральной совокупности 
имеет нормальное распределение с параметрами 
. Случайная величина 
– разность выборочных средних – имеет нормальное распределение (как разность нормально распределенных случайных величин) с параметрами
.Теперь можно заключить случайную величину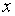 
в интервал
, где 
, и найти число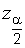 
, пользуясь таблицей функции Лапласа (прил. 2), из условия
. Тогда интервал для разности 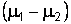таков:
.
Если значения и неизвестны, но объемы выборок достаточно велики ( 
), то также пользуются описанной процедурой, подставляя вместо и исправленные выборочные дисперсии 
и 
, определенные по выборкам.
40. 
43. Проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей
Рассмотрим две случайные величины Х и У, каждая из которых подчиняется нормальному закону с дисперсиями 
. Пусть из этих генеральных совокупностей извлечены две выборки объёмами п1 и п2. Проверим гипотезу Н0 о том, что 
относительно альтернативной гипотезы Н1, заключающейся в том, что 
Однако, мы располагаем только выборочными дисперсиями 
= 
и 
= 
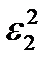. Задача проверки гипотезы Н0 сводится к сравнению выборочных дисперсий.
Для построения критической области с выбранной надёжностью необходимо исследовать совместный закон распределения оценок 
и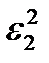 
. Таким законом распределения является распределение Фишера – Снедекора (или F - распределение)
Рассмотрим случайную величину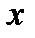 
, распределённую нормально с математическим ожиданием Х и с дисперсией 
. Произведём две независимые выборки объёмами п1 и п2. Для оценки 
используют выборочные дисперсии. Случайную величину, определяемую отношением 
, называют величиной с распределением Фишера-Снедекора. Имеются таблицы для дифференциального закона распределения Фишера-Снедекора, которые зависят лишь от объёма выборки и уровня значимости
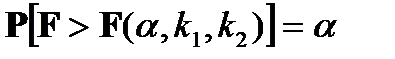, где k1 = n1 -1, k2 = n2 -1.
Вернёмся снова к задаче проверки гипотезы о равенстве дисперсий. Сначала нужно вычислить выборочные дисперсии. Найдём отношение F=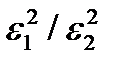 
, причём в числителе поставим большую из двух оценок дисперсии. Выберем уровень значимости 
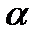и из таблиц находим число F 
которое сравнивается с вычисленным F. Если окажется, что 
, то проверяема гипотеза Н0 отвергается, в противном случае делается вывод о том, что наблюдения не противоречат проверяемой гипотезе.
44. Проверяется гипотеза вида 
. При неизвестных, но равных дисперсиях. При неравных объемах выборок 
статистика критерия имеет вид
, где 
, 
, 
, 
, или
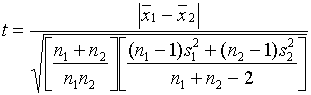. В случае нормального закона эта статистика в случае справедливости 
должна подчиняться распределению Стьюдента с числом степеней свободы 
, то есть 
.
При равных объемах выборок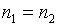 
статистика принимает вид
= 
, а 
.
45. Проверяется гипотеза вида . При известных дисперсиях. Применение критерия сравнения двух выборочных средних при известных и равных дисперсиях предусматривает вычисление статистики
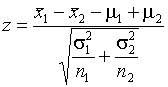, где 
, 
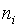- объем 
-й выборки, 
В случае принадлежности наблюдений нормальным законам статистика 
подчиняется стандартному нормальному закону.
46. Критерий согласия 
.
Существует несколько критериев согласия для проверки законов распределения случайной величины. Это критерии Колмогорова, Смирнова,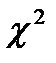 
Пирсона и др. Мы остановимся лишь на критерии Пирсона – это наиболее часто употребляемый критерий для проверки закона распределения случайной величины. Сначала нужно разбить всю область изменения случайной величины на l интервалов (бин). Затем нужно подсчитать сколько этих величин попадает в каждый бин, то есть подсчитать эмпирические частоты тк. Чтобы вычислить теоретические частоты нужно вероятность попадания в каждый бин рк умножить на объём выборки п. Таким образом, статистика 
является случайной величиной, подчиняющейся закону 
с 
степенями свободы.В последней формуле r – число параметров распределния, определяемы по выборке. Для нормального закона – это два параметра, для закона Пуассона – один и т.д.
Рассчитав значения 
и выбрав уровень значимости 
, по таблице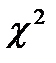 
-распределения определяют 
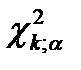. Если 
, то гипотезу Н0 отвергают, если 
то гипотезу принимают.
47. Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных 
на зависимую переменную 
. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. На практике линия регрессии чаще всего ищется в виде линейной функции 
(линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых от их оценок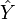 
(имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда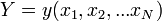 
.
Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:
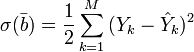Условие минимума функции невязки:
Полученная система является системой 
линейных уравнений с неизвестными 
Если представить свободные члены левой части уравнений матрицей 
а коэффициенты при неизвестных в правой части матрицей
то получаем матричное уравнение: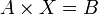 
, которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии: 
Для получения наилучших оценок необходимо выполнение предпосылок МНК.