Основным источником реактивной мощности в системе являются генераторы электростанций, вырабатывающие около 60 % требуемой реактивной мощности. Располагаемая реактивная мощность электростанций ЭС недостаточна для покрытия общей потребности ЭС в реактивной мощности [1]. В связи с этим возникает необходимость установки дополнительных источников реактивной мощности (компенсирующих устройств).
Компенсация реактивных нагрузок является одним из эффективных способов снижения потерь активной мощности и электроэнергии в элементах электрических сетей и улучшения качества электроэнергии по отклонению напряжения за счет уменьшения потерь напряжения в элементах электрических сетей. Эффект достигается за счет разгрузки элементов электрических сетей от источника питания до места установки компенсирующих устройств по реактивной мощности.
Оптимальное распределение компенсирующих устройств по сети является сложной технико-экономической задачей и в проекте не рассматривается.
В соответствии с [2] предельное значение коэффициента реактивной мощности на шинах 6-20 кВ понижающих подстанций составляет  = 0,4.
= 0,4.
Таким образом, если на подстанциях проектируемой сети, на шинах 6 (10) кВ которых не выполняется условие
 , (1.5)
, (1.5)
необходимо установить компенсирующие устройства мощностью
 . (1.6)
. (1.6)
Основным типом компенсирующих устройств, устанавливаемых на шинах 6-10 кВ понижающих подстанций, являются конденсаторные батареи.
Для некоторых из рассматриваемых подстанций вычисленная мощность конденсаторных батарей, по выражению (2.6), может оказаться отрицательной. Это свидетельствует о том, что установка конденсаторных батарей на данной подстанции не требуется.
Число конденсаторных батарей на шинах 6-10 кВ понижающей подстанций должно быть четным и определяется выражением:
 . (1.7)
. (1.7)
где  – мощность, выдаваемая батареей при напряжении
– мощность, выдаваемая батареей при напряжении  , принимается по справочным данным (таблица П.1).
, принимается по справочным данным (таблица П.1).
В заключение раздела определяются расчётные нагрузки подстанций с учетом мощности установленных конденсаторных батарей. Мощность конденсаторных батарей снижает общую (расчётную) мощность подстанции:
 . (1.8)
. (1.8)
Задание 1
На рисунке 1.1 показана схема географического расположения источника питания района и пунктов потребления электроэнергии. Нагрузки подстанций равны:  =36 МВт,
=36 МВт,  39 МВт,
39 МВт,  МВт,
МВт,  =17 МВт,
=17 МВт,  41 МВт. Определить мощности нагрузок, рассчитать баланс активной мощности в сети и расставить компенсирующие устройства на шинах 10 кВ понижающих подстанций.
41 МВт. Определить мощности нагрузок, рассчитать баланс активной мощности в сети и расставить компенсирующие устройства на шинах 10 кВ понижающих подстанций.

Рисунок 1.1 – Схема географического расположения
Решение:
Расчет нагрузок.
Определяем коэффициент реактивной мощности по формуле (1.1) сos(j)=0,8: tg(φ)=tg(arccos(0,86))=0,75.
Реактивная и полная нагрузка узла 2:
Qнб1=36∙0,75=27 Мвар;
Sнб1=36/0,8=48,75 МВ∙А.
Расчеты для остальных узлов сводим в таблицу 1.1.
Таблица 1.1 – Определение заданных нагрузок
| № n/c |  , MBт , MBт
| 
| 
|  , Mвар , Mвар
|  , MB·A , MB·A
|
| 0,8 | 0,75 | 27,00 | 45,00 | ||
| 0,8 | 0,75 | 29,25 | 48,75 | ||
| 0,8 | 0,75 | 16,50 | 27,50 | ||
| 0,8 | 0,75 | 12,75 | 21,25 | ||
| 0,8 | 0,75 | 30,75 | 51,25 | ||
| Итого | 116,25 | 193,75 |
Баланс активной мощности
Определим суммарную нагрузку сети:
 36+39+22+17+41=155 МВт.
36+39+22+17+41=155 МВт.
Суммарные потери активной мощности в элементах сети:
 0,05·155=7,75 МВт.
0,05·155=7,75 МВт.
Общее потребление активной мощности проектируемого района электрической сети:
 0,95·155+7,75=155 МВт.
0,95·155+7,75=155 МВт.
Так как ограничений по мощности источника питания не имеется, то баланс активной мощности в проектируемом районе электрической сети соблюдается.
Расстановка компенсирующих устройств
Определяем мощность компенсирующих устройств устанавливаемых на каждой из подстанций проектируемого района в соответствии с предельным значением коэффициента реактивной мощности 0,4:
 36·(0,75-0,4)=12,60 Мвар;
36·(0,75-0,4)=12,60 Мвар;  39·(0,75-0,4)=13,65 Мвар;
39·(0,75-0,4)=13,65 Мвар;
 22·(0,75-0,4)=7,7 Мвар;
22·(0,75-0,4)=7,7 Мвар;  17·(0,75-0,4)=5,95 Мвар;
17·(0,75-0,4)=5,95 Мвар;
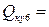 41·(0,75-0,4)=14,35 Мвар;
41·(0,75-0,4)=14,35 Мвар;
Определим число конденсаторных батарей на каждой из подстанции:
 12,60/3,15=4,0
12,60/3,15=4,0  13,65/2,25=6,07
13,65/2,25=6,07
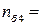 7,7/1,35=5,7
7,7/1,35=5,7  5,95/3,15=1,9
5,95/3,15=1,9
 14,35/1,8=7,97
14,35/1,8=7,97
| На п/ст 2 устанавливаем | БК | типа УК-10,5- | ||
| на п/ст 3 устанавливаем | БК | типа УК-10,5- | ||
| на п/ст 4 устанавливаем | БК | типа УК-10,5- | ||
| на п/ст 5 устанавливаем | БК | типа УК-10,5- | ||
| на п/ст 6 устанавливаем | БК | типа УК-10,5- |
Результаты расстановки конденсаторных батарей и определения расчётных нагрузок подстанций сведем в таблицу 1.2.
Таблица 1.2 – Расчетные нагрузки с учетом компенсации реактивной мощности
| № п/ст |  , Мвар , Мвар
|  , Мвар , Мвар
|  , МВт , МВт
|  , Мвар , Мвар
|  , Мвар , Мвар
|  , МВ·А , МВ·А
|
| 12,60 | 12,6 | 27,00 | 14,40 | 38,77 | ||
| 13,65 | 13,5 | 29,25 | 15,75 | 42,06 | ||
| 7,70 | 8,1 | 16,50 | 8,40 | 23,55 | ||
| 5,95 | 6,3 | 12,75 | 6,45 | 18,18 | ||
| 14,35 | 14,4 | 30,75 | 16,35 | 44,14 | ||
| Итого | 54,25 | 54,90 | 155,00 | 116,25 | 61,35 | 166,71 |
Вопросы к заданию 1
1. Какова связь между балансом активной мощности и регулированием частоты?
2. Каково назначение батарей конденсаторов и синхронных компенсаторов в электрических сетях?
3. Каковы критерии расстановки КУ?
Тема 2
Расчет потокораспределения активной мощности, выбор номинального напряжения линий
Теоретическая часть
Предварительный расчет потокораспределения производится для режима наибольших нагрузок. Порядок расчета потокораспределения зависит от типа линий, образующих сеть.
Расчет потокораспределения радиально-магистральных линий делают на основании первого закона Кирхгофа, двигаясь от наиболее удаленных потребителей к источнику. Так как расчет приближенный, то потерями мощности пренебрегают.
Кольцевую линию вначале условно «разрезают» по источнику и разворачивают, превращая кольцевую линию в линию с двухсторонним питанием. Далее определяют поток мощности на одном из головных участков (условно считая, что вся линия однородна), по формуле:
 , (2.1)
, (2.1)
где  – поток мощности на головном участке;
– поток мощности на головном участке;  – i -тая нагрузка;
– i -тая нагрузка;  – общая длина кольцевой линии;
– общая длина кольцевой линии;  – расстояние от места подключения i -той нагрузки до источника, противоположного рассматриваемому головному участку.
– расстояние от места подключения i -той нагрузки до источника, противоположного рассматриваемому головному участку.
Определив поток мощности на головном участке, далее по первому закону Кирхгофа определяют потоки на остальных участках, двигаясь к противоположному источнику. Потерями также пренебрегают. В конце расчета рекомендуется сделать проверку. Для этого нужно по формуле (4.1) определить поток мощности на противоположном головном участке и сравнить его с потоком мощности, полученным по первому закону Кирхгофа.
Если от кольцевой линии, где делается расчет потокораспределения, отходит радиальная или магистральная линия, то все нагрузки этой линии считаются находящимися в точке подключения линии.
Если кольцевая линия получает питание по радиальной, то «разрез» делают в точке подключения кольцевой линии к радиальной.
В случае сложно-замкнутой сети ее предварительно преобразуют в простую замкнутую сеть или проводят расчет потокораспределения методом узловых потенциалов, используя вычислительную технику.
Номинальное напряжение можно предварительно определить по известным передаваемой мощности Р, МВт, и длине линии  , км, по формуле Стилла:
, км, по формуле Стилла:
 . (2.2)
. (2.2)
Эта формула приемлема для линий длиной до 250 км и передаваемых мощностей, не превышающих 60 МВт. В случае больших мощностей, передаваемых на расстояние до 1000 км, используется формула А. М. Залесского:
 . (2.3)
. (2.3)
Г. А. Илларионов предложил для предварительного определения  следующее выражение:
следующее выражение:
 . (2.4)
. (2.4)
В отличие от эмпирических выражений (2.2), (2.3) формула (2.4) дает удовлетворительные результаты для всей шкалы номинальных напряжений от 35 до 1150 кВ.
Задание 2
Определить потокораспределение активной мощности и номинальное напряжение линий для схемы варианта 1 рисунок 2.1.


Рисунок 2.1– Варианты схемы сети
Решение:
Найдем по первому закону Кирхгофа мощности в линиях, МВт:
 =41+17+22=80;
=41+17+22=80;
 =41+17=58;
=41+17=58;
 =41;
=41;
 =36+39=75;
=36+39=75;
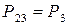 = 39.
= 39.
Номинальное напряжение можно предварительно определить по эмпирическому выражению (2.2). Напряжения, кВ, определенные по этому выражению, для линий сети равны:
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
 кВ;
кВ;
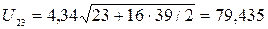 кВ.
кВ.
Номинальные напряжения определенные по эмпирическому выражению (2.4):
 108,64 кВ;
108,64 кВ;
 96,034 кВ
96,034 кВ
 84,94 кВ;
84,94 кВ;
 109,55 кВ;
109,55 кВ;
 81,66 кВ.
81,66 кВ.
Обе формулы дают близкие результаты.
Для схемы варианта 1 по результатам расчета выбираем номинальное напряжение 110 кВ на всех участках.
Таблица 2.1 – Выбор напряжений для схемы варианта 1
| Участок | L, км | P, МВт | U', кВ | Uном, кВ |
| 22,5 | 108,64 | |||
| 22,5 | 96,03 | |||
| 84,94 | ||||
| 109,54 | ||||
| 81,66 |
Задание 3
Определить потокораспределение активной мощности и номинальное напряжение линий для схемы варианта 2 рисунок 2.1.
Решение:
Вариант 2 представляет собой смешанную схему, состоящую из кольца 1231 и магистрального участка 1456.
Магистральный участок
Потокораспределения активной мощности и номинальные напряжения в линиях магистрального участка 1456 рассчитаны в задание 2.
Кольцо 1231
В кольцевой сети условно «разрезаем» источник и разворачиваем кольцо, превращая кольцевую сеть в магистральную линию с двухсторонним питанием (рисунке 4.3).

Рисунок 2.2 – Расчетная схема кольца 1231
Для кольца 1231 находим сначала активные мощности на головных участках по активным мощностям и длинам линий по выражению (2.1):

 =44,45 МВт;
=44,45 МВт;  =30,55 МВт.
=30,55 МВт.
Правильность найденных значений  и
и  подтверждается следующей проверкой:
подтверждается следующей проверкой:
 +
+  =
=  ;
;
 +
+  =44,45+30,55=75 МВт;
=44,45+30,55=75 МВт;  =36+39=75 МВт.
=36+39=75 МВт.
Активные мощности на головных участках определены правильно.
Мощность в линии 23 определим в соответствии с первым законом Кирхгофа:
 = 44,45–36 = 8,45 МВт.
= 44,45–36 = 8,45 МВт.
Узел 3 является точкой потокораздела кольца 1231 3.
Номинальное напряжение по выражению (2.2) равны:
 кВ;
кВ;
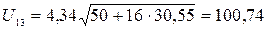 кВ;
кВ;
 кВ.
кВ.
Номинальные напряжения, определенные по эмпирическому выражению (2.4):
 117,11 кВ
117,11 кВ
 104,35 кВ;
104,35 кВ;
 56,11 кВ.
56,11 кВ.
Обе формулы дают близкие результаты.
Для схемы варианта 2 по результатам расчета выбираем номинальное напряжение 110 кВ на всех участках.
Таблица 2.1 – Выбор напряжений для схемы варианта 2
| Участок | L, км | P, МВт | U', кВ | Uном, кВ |
| 22,5 | 108,64 | |||
| 22,5 | 96,03 | |||
| 84,94 | ||||
| 44,45 | 117,11 | |||
| 30,55 | 104,35 | |||
| 8,45 | 56,11 |
Вопросы к заданию 2, 3
1. От каких факторов зависит экономически целесообразное номинальное напряжение проектируемой сети?
2. Каковы преимущества и недостатки применения более высокого номинального напряжения?
3. Каковы недостатки применения более высокого номинального напряжения?
Тема 3
Баланс реактивной мощности. Расчет потокораспределения реактивной мощности.
Теоретическая часть
Решить вопрос о необходимости установки компенсирующих устройств в проектируемой сети сверх установленных по условию (1.6) следует до выполнения расчетов параметров элементов сети, так как компенсация реактивной мощности влияет на передаваемые по элементам сети мощности и может влиять на их выбираемые параметры, а также влияет на потери мощности и напряжения в элементах сети.
Потребление реактивной мощности в проектируемой сети в период наибольших нагрузок складывается из расчетных реактивных нагрузок в пунктах потребления электроэнергии (с учетом установленных конденсаторных батарей по условию не превышения предельных значений коэффициента реактивной мощности) и потерь реактивной мощности в элементах электрической сети (линиях и понижающих трансформаторах) с учетом зарядных мощностей линий. При определении одновременно потребляемой реактивной мощности следует также учитывать несовпадение по времени суток наибольших нагрузок отдельных потребителей. При четырех и более пунктах потребления среднестатистическое значение коэффициента одновременности реактивных нагрузок на шинах до 220 кВ источника питания составляет 0,98.
Таким образом, наибольшая суммарная реактивная мощность, потребляемая в проектируемом районе электрической сети, составляет:
 , (3.1)
, (3.1)
где  – коэффициент одновременности наибольших реактивных нагрузок подстанций (
– коэффициент одновременности наибольших реактивных нагрузок подстанций ( =0,98);
=0,98);  – наибольшая расчетная реактивная нагрузка i -го пункта (с учетом установленных конденсаторных батарей по условию (1.6)); n – число пунктов потребления электроэнергии проектируемой электрической сети;
– наибольшая расчетная реактивная нагрузка i -го пункта (с учетом установленных конденсаторных батарей по условию (1.6)); n – число пунктов потребления электроэнергии проектируемой электрической сети;  – суммарные потери в трансформаторах подстанций проектируемой сети;
– суммарные потери в трансформаторах подстанций проектируемой сети;  – потери реактивной мощности в i -й линии электропередачи проектируемой сети;
– потери реактивной мощности в i -й линии электропередачи проектируемой сети;  – зарядная мощность i -й линии электропередачи проектируемой сети; m – число линий электропередачи в сети.
– зарядная мощность i -й линии электропередачи проектируемой сети; m – число линий электропередачи в сети.
В электрических сетях номинальным напряжением до 220 кВ основным типом подстанций являются подстанции с двухобмоточными трансформаторами, для которых при двух параллельно включенных трансформаторах и коэффициенте аварийной перегрузки 1,4 потери реактивной мощности приближенно оцениваются в размере 8 % от полной нагрузки подстанции  [3].
[3].
Мощность нагрузки i -й подстанции на пути от источника питаний может проходить через несколько трансформаций. Если считать, что на каждой из них теряется 8 % от полной мощности этой нагрузки, то можно оценить суммарные потери реактивной мощности в трансформаторах подстанций сети следующим образом:
 , (3.2)
, (3.2)
где  – число трансформаций нагрузки i -й подстанции (
– число трансформаций нагрузки i -й подстанции ( ) на пути от источника питания до ее шин низшего напряжения.
) на пути от источника питания до ее шин низшего напряжения.
Вторая составляющая потерь реактивной мощности – потери в линиях электропередачи – существенно зависит от передаваемой по линии мощности и длины линии; зарядная мощность линий – от длины линии. Обе эти величины зависят от напряжения электропередачи, причем потери мощности обратно пропорциональны, а зарядная мощность прямо пропорциональна квадрату напряжения линии электропередачи. Вследствие этого, соотношение потерь и генерации реактивной мощности в линиях существенно различается для линий разных номинальных напряжений. При этом сечение проводов линий практически не оказывает влияния на это соотношение.
Зарядная мощность линии длиной L с числом цепей  определяется выражением:
определяется выражением:
 , (3.3)
, (3.3)
где  – удельная генерация реактивной мощности линий напряжением 220 кВ – 0,14 Мвар/км, напряжением 110 кВ – 0,036 Мвар/км.
– удельная генерация реактивной мощности линий напряжением 220 кВ – 0,14 Мвар/км, напряжением 110 кВ – 0,036 Мвар/км.
Соотношение между потерями и генерацией реактивной мощности в линиях зависит от отношения передаваемой активной мощности по одной цепи линии к натуральной мощности линии  .
.
Откуда при известном значении передаваемой по линии активной мощности  и зарядной мощности линии потери реактивной мощности в линии находятся по выражению:
и зарядной мощности линии потери реактивной мощности в линии находятся по выражению:
 , (3.4)
, (3.4)
В качестве средних значений натуральной мощности для линий 110 кВ может быть принято 30 МВт, линий 220 кВ – 130 МВт.
Анализ значений разности между зарядной мощностью и потерями реактивной мощности в линиях 110 кВ показывает, что на этой стадии расчета в линиях 110 кВ допускается принимать равными величины потерь и генерации реактивной мощности при условии передачи по линиям активной мощности, существенно не превышающей значения натуральной мощности.
Полученное по (3.1) значение суммарной потребляемой реактивной мощности в проектируемом районе электрической сети  сопоставляется со значением реактивной мощности, которую экономически целесообразно передать с шин источника питания в проектируемую электрическую сеть
сопоставляется со значением реактивной мощности, которую экономически целесообразно передать с шин источника питания в проектируемую электрическую сеть  определяемым по суммарному потреблению активной мощности в проектируемой электрической сети и коэффициенту реактивной мощности источника питания, указанному в задании на проект:
определяемым по суммарному потреблению активной мощности в проектируемой электрической сети и коэффициенту реактивной мощности источника питания, указанному в задании на проект:
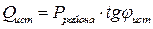 . (3.5)
. (3.5)
Если  то необходимость в установке компенсирующих устройств в узлах проектируемой сети (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности) отсутствует, так как системные источники реактивной мощности полностью покрывают всю потребность в ней.
то необходимость в установке компенсирующих устройств в узлах проектируемой сети (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности) отсутствует, так как системные источники реактивной мощности полностью покрывают всю потребность в ней.
Если  то в проектируемой сети должны быть установлены компенсирующие устройства (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности), суммарная мощность которых определяется из условия выполнения баланса реактивной мощности:
то в проектируемой сети должны быть установлены компенсирующие устройства (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности), суммарная мощность которых определяется из условия выполнения баланса реактивной мощности:
 . (3.6)
. (3.6)
Конденсаторные батареи суммарной мощностью  необходимо распределить между подстанциями проектируемой сети. С учетом дискретности суммарная мощность устанавливаемых батарей конденсаторов должна быть не менее чем
необходимо распределить между подстанциями проектируемой сети. С учетом дискретности суммарная мощность устанавливаемых батарей конденсаторов должна быть не менее чем  .
.
Расстановка компенсирующих устройств производиться по условию равенства коэффициентов реактивной мощности нагрузок на шинах 10 кВ, удовлетворяющему условию выполнения баланса реактивной мощности в проектируемой сети:
 . (3.7)
. (3.7)
где  – действительные реактивные нагрузки подстанций с учетом мощности установленных конденсаторных батарей по условию (1.5).
– действительные реактивные нагрузки подстанций с учетом мощности установленных конденсаторных батарей по условию (1.5).
Тогда мощность устанавливаемых конденсаторных батарей (сверх установленных по условию (1.6)) на i -й подстанции
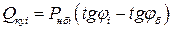 . (3.8)
. (3.8)
Для некоторых из рассматриваемых подстанций вычисленная мощность конденсаторных батарей может оказаться отрицательной. Это свидетельствует о том, что коэффициент реактивной мощности достаточно низок и установка конденсаторных батарей на шинах 10 кВ данной подстанции по условию равенства коэффициентов реактивной мощности нагрузок на шинах 10 кВ не требуется. Данная подстанция должна быть исключена из числа n в выражении (3.8), и соответственно пересчитаны значения  и
и  .
.
Определенные в результате расчета мощности  , округляются до стандартных значений так, чтобы сумма
, округляются до стандартных значений так, чтобы сумма  соответствовала
соответствовала  .
.
В заключение определяются действительные реактивные нагрузки подстанций  с учетом мощности установленных конденсаторных батарей по условию не превышения предельных значений коэффициента реактивной мощности (1.5) и условию выполнения баланса реактивной мощности в проектируемой сети (3.6) и полные нагрузки подстанций
с учетом мощности установленных конденсаторных батарей по условию не превышения предельных значений коэффициента реактивной мощности (1.5) и условию выполнения баланса реактивной мощности в проектируемой сети (3.6) и полные нагрузки подстанций  . Затем необходимо определить приведенные к шинам высшего напряжения нагрузки подстанций
. Затем необходимо определить приведенные к шинам высшего напряжения нагрузки подстанций  , пренебрегая потерями активной мощности в трансформаторах и принимая потери реактивной мощности в трансформаторах равными 8 % от полной нагрузки подстанции, в соответствии с выражением
, пренебрегая потерями активной мощности в трансформаторах и принимая потери реактивной мощности в трансформаторах равными 8 % от полной нагрузки подстанции, в соответствии с выражением
 . (3.9)
. (3.9)
Задание 4
Оценить баланс реактивной мощности для сети вариант 1 и определить потокораспределение реактивной мощности. Коэффициент мощности системы, в которую входит проектируемая сеть, равен  =0,9.
=0,9.
Решение:
Оцениваем баланс реактивной мощности.
Т.к. активная мощность в линиях отличается от значения натуральной мощности, следует учитывать величины потерь и генерации реактивной мощности.
Находим зарядную мощность линии по выражению (3.3):
 2∙0,036∙30=2,16 Мвар;
2∙0,036∙30=2,16 Мвар;  2∙0,036∙23=1,656 Мвар;
2∙0,036∙23=1,656 Мвар;
 2∙0,036∙22,5=1,62 Мвар;
2∙0,036∙22,5=1,62 Мвар;  2∙0,036∙22,5=1,62 Мвар;
2∙0,036∙22,5=1,62 Мвар;
 2∙0,036∙30=2,16 Мвар;
2∙0,036∙30=2,16 Мвар;
 9,216 Мвар.
9,216 Мвар.
Находим потери реактивной мощности в линиях по выражению (3.4):
 Мвар;
Мвар;  Мвар;
Мвар;
 Мвар;
Мвар;  Мвар;
Мвар;
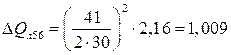 Мвар;
Мвар;
 Мвар.
Мвар.
Находим суммарные потери реактивной мощности в трансформаторах подстанций сети по выражению (3.2):
 0,08∙166,705=13,336 Мвар.
0,08∙166,705=13,336 Мвар.
Находим наибольшую суммарную реактивную мощность, потребляемую в проектируемом районе электрической сети по выражению (3.1):
 0,98∙61,35+13,336+9,478-9,216=73,721 Мвар.
0,98∙61,35+13,336+9,478-9,216=73,721 Мвар.
Величина реактивной мощности, поступающей с шин источника питания в проектируемую электрическую сеть по выражению (3.5) равна:
 155∙0,48=74,4 Мвар, где
155∙0,48=74,4 Мвар, где  0,48.
0,48.
Т.к. 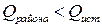 , то нет необходимости установки дополнительных КУ (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности).
, то нет необходимости установки дополнительных КУ (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности).
Определяем действительные реактивные нагрузки подстанций по выражению (3.9) а результаты сводим в таблицу 3.1.
Таблица 3.1 – Действительные мощности нагрузок подстанций
| № п/ст |  , МВт , МВт
|  , МВар , МВар
|  , Мвар , Мвар
|  , Мвар , Мвар
|  , МВ·А , МВ·А
|  , Мвар , Мвар
| 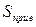 , МВ·А , МВ·А
|
| 27,00 | 12,6 | 14,40 | 38,77 | 17,50 | 40,03 | ||
| 29,25 | 13,5 | 15,75 | 42,06 | 19,11 | 43,43 | ||
| 16,50 | 8,1 | 8,40 | 23,55 | 10,28 | 24,28 | ||
| 12,75 | 6,3 | 6,45 | 18,18 | 7,90 | 18,75 | ||
| 30,75 | 14,4 | 16,35 | 44,14 | 19,88 | 45,57 | ||
| Итого | 54,90 | 61,35 | 166,70 | 74,67 | 172,06 |
Расчет потокораспределения реактивной мощности.
 =10,28+7,9+19,88=38,06 Мвар;
=10,28+7,9+19,88=38,06 Мвар;
 =7,9+19,88=27,78 Мвар;
=7,9+19,88=27,78 Мвар;
 =19,88 Мвар;
=19,88 Мвар;
 =17,5+19,11=36,61 Мвар;
=17,5+19,11=36,61 Мвар;
 =19,11 Мвар.
=19,11 Мвар.
Расчет потокораспределения полной мощности.
Находим по выражению (1.3):
 88,59 MB∙A;
88,59 MB∙A;
 64,31 MB∙A;
64,31 MB∙A;
 45,57 MB∙A;
45,57 MB∙A;
 83,46 MB∙A;
83,46 MB∙A;
 43,43 MB∙A.
43,43 MB∙A.
Задание 5
Оценить баланс реактивной мощности для сети вариант 2 и определить потокораспределение реактивной мощности. Коэффициент мощности системы, в которую входит проектируемая сеть, равен  =0,9.
=0,9.
Решение:
Оцениваем баланс реактивной мощности.
Магистральный участок
Зарядная мощность и потери реактивной мощности в линиях магистрального участка 1456 рассчитаны в задание 4.
 1,62 Мвар;
1,62 Мвар;  1,62 Мвар;
1,62 Мвар;  2,16 Мвар.
2,16 Мвар.
 Мвар;
Мвар; 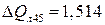 Мвар;
Мвар;  Мвар.
Мвар.
Кольцо 1231
Находим зарядную мощность линии по выражению (3.3):
 ∙0,036∙30=1,08 Мвар;
∙0,036∙30=1,08 Мвар;
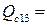 0,036∙50=1,8 Мвар
0,036∙50=1,8 Мвар
 0,036∙23=0,828 Мвар.
0,036∙23=0,828 Мвар.
 9,108 Мвар.
9,108 Мвар.
Находим потери реактивной мощности в линиях по выражению (3.4):
 Мвар;
Мвар;
 Мвар;
Мвар;
 Мвар;
Мвар;
 Мвар.
Мвар.
Суммарные потери реактивной мощности в трансформаторах подстанций сети по выражению (3.2):
 13,336 Мвар.
13,336 Мвар.
Находим наибольшую суммарную реактивную мощность, потребляемую в проектируемом районе электрической сети по выражению (3.1):
 0,98∙61,35+13,336+9,707-9,108=74,058 Мвар.
0,98∙61,35+13,336+9,707-9,108=74,058 Мвар.
Величина реактивной мощности, поступающей с шин источника питания в проектируемую электрическую сеть по выражению (3.5) равна:
 155∙0,48=74,4 Мвар, где
155∙0,48=74,4 Мвар, где  0,48.
0,48.
Т.к. 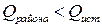 , то нет необходимости установки дополнительных КУ (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности).
, то нет необходимости установки дополнительных КУ (сверх установленных по условию не превышения предельных значений коэффициента реактивной мощности).
Действительные реактивные нагрузки подстанций будут такими же, как для варианта 1 (таблица 3.1).
Расчет потокораспределения реактивной мощности.
Магистральный участок
Потокораспределение реактивной мощности магистрального участка 1456 рассчитаны в задание 4:
 38,06 Мвар;
38,06 Мвар;
 27,78 Мвар;
27,78 Мвар;
 19,88 Мвар;
19,88 Мвар;
Кольцо 1231
Потокораспределение реактивной мощности кольца 1231 рассчитываем аналогично потокам активной мощности кольца 1231 в задание 3.
Реактивные мощности на головных участках:
 =21,68 Мвар;
=21,68 Мвар;  =14,93 Мвар.
=14,93 Мвар.
Правильность найденных значений  и
и 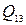 подтверждается следующей проверкой:
подтверждается следующей проверкой:
 +
+ 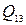 =
=  ;
;
 +
+ 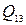 =21,68+14,93=36,61 Мвар;
=21,68+14,93=36,61 Мвар;  =17,5+19,11=36,61 Мвар.
=17,5+19,11=36,61 Мвар.
Реактивные мощности на головных участках определены правильно.
Мощность в линии 23 определим в соответствии с первым законом Кирхгофа:
 = 21,68–17,5 = 4,18 МВт.
= 21,68–17,5 = 4,18 МВт.
Расчет потокораспределения полной мощности.
Находим по выражению (1.3):
Магистральный участок
 88,59 MB∙A;
88,59 MB∙A;
 64,31 MB∙A;
64,31 MB∙A;
 45,57 MB∙A.
45,57 MB∙A.
Кольцо 1231
 49,46 MB∙A;
49,46 MB∙A;
 34 MB∙A;
34 MB∙A;
 9,43 MB∙A.
9,43 MB∙A.
Вопросы к заданиям 4, 5
1. Какова связь между балансом реактивной мощности и регулированием напряжения?
2. При каком условии в линиях 110 кВ допускается принимать равными величины потерь и генерации реактивной мощности?
3. В электрических сетях двух номинальных напряжений (например, 220/110 кВ) следует в первую очередь устанавливать компенсирующие устройства на шинах 10 кВ подстанций сети более низкого номинального напряжения (110 кВ) или более высокого (220 кВ)?
Тема 4
Выбор сечений и марок проводов воздушных линий. Проверка сечений проводов по условиям технических ограничений
Теоретическая часть
Все проводники обладают активным сопротивлением, поэтому при пропускании тока греются, то есть часть передаваемой по линии электропередачи мощности расходуется на этот нагрев. При этом суммарные потери электроэнергии в электрических сетях достигают колоссальных объемов. Существует только один способ снижения этих потерь – это уменьшение активного сопротивления проводников.
При обычных температурах уменьшить сопротивление проводника можно только путем увеличения его сечения. Но увеличение сечения влечет за собой увеличение стоимости ЛЭП. Таким образом, увеличению сечения сопутствуют два конкурирующих фактора. С одной стороны это снижение затрат на компенсацию потерь электроэнергии. С другой – увеличение затрат на сооружение ЛЭП. Сечение, которое соответствует минимуму затрат, называют экономически целесообразным.
На воздушных линиях предусматривается применение только сталеалюминиевых проводов марки АС, маркируемых в соответствии с ГОСТ 839-80Е.
Экономически целесообразное сечение проводов  линии определяется выражением
линии определяется выражением
 (4.1)
(4.1)
где  – расчетный ток одной цепи линии;
– расчетный ток одной цепи линии;  – норматив экономической плотности тока. Нормированные значения плотности тока для ВЛ приведены в таблице П.2.
– норматив экономической плотности тока. Нормированные значения плотности тока для ВЛ приведены в таблице П.2.
Значение  определяется по выражению
определяется по выражению
 , (4.2)
, (4.2)
где  – наибольший ток одной цепи линии на пятый год ее эксплуатации;
– наибольший ток одной цепи линии на пятый год ее эксплуатации;  – коэффициент, учитывающий изменение нагрузки по годам эксплуатации линии за расчетный период (10 лет). Для линий 110-220 кВ значение
– коэффициент, учитывающий изменение нагрузки по годам эксплуатации линии за расчетный период (10 лет). Для линий 110-220 кВ значение  , принимается равным 1,05, что соо
, принимается равным 1,05, что соо