Теорема 1. В любом линейном пространстве нулевой вектор единственный.
Доказательство. Пусть 
X, причём для любых векторов 
X, справедливы равенства
и 
, т.е. и вектор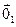 
, и вектор 
являются нулевыми векторами пространства X. Отсюда получаем: 
. Здесь мы воспользовались коммутативностью сложения, а также приведёнными равенствами, положив 
. Теорема доказана.
Теорема 2. Для любого вектора 
линейного пространства X противоположный к нему вектор единственный.
Доказательство. Пусть 
X, причём 
и 
. Отсюда следует, что
. Здесь мы воспользовались, кроме приведённых равенств ещё 2-ой и 3-ей аксиомами. Теорема доказана.
Теорема 3. Для любого вектора линейного пространства X справедливо равенство 
.
Доказательство. Воспользуемся аксиомой 7: 
. Пусть 
- вектор, противоположный к вектору 
, т.е. 
. Используем полученное равенство
. В результате получим: 
. Здесь мы воспользовались аксиомами 1, 2 и 3.
Теорема доказана.
Теорема 4. Вектор, противоположный к вектору линейного пространства X, равен вектору 
.
Доказательство. Действительно, вектор удовлетворяет аксиоме 4: 
. Здесь мы воспользовались аксиомами 5, 7 и теоремой 3. Из теоремы 2 следует, что вектор, противоположный к вектору , равен . Теорема доказана.
Замечание. В дальнейшем вектор, противоположный к вектору , будем обозначать так: 
.
Задача 1. Докажите, что если 
, то или 
, или 
.
Задача 2. Докажите, что 
для любого числа 
K.
§2 Линейная зависимость и линейная независимость системы векторов.
Определение 1. Пусть X - линейное пространство над полем K, 
X, 
K. Выражение вида 
будем называть линейной комбинацией векторов 
с коэффициентами 
.
Запись: 
ЛК 
будет означать, что вектор является линейной комбинацией векторов .
|
|
Замечание. Очевидно, линейная комбинация линейных комбинаций векторов также является
линейной комбинацией этих векторов, т.к. 
. Какими аксиомами линейного пространства мы здесь воспользовались?
Определение 2. Пусть X - линейное пространство над полем K. Множество всех линейных комбинаций векторов X будем называть линейной оболочкой, натянутой на векторы и обозначать так: 
. Таким образом,
K 
.
Очевидно, 
X.
Определение 3. Совокупность векторов X будем называть линейно зависимой, если существуют числа K, не равные нулю одновременно и такие, что 
.
В противном случае совокупность будем называть линейно независимой.
Таким образом, одна и та же совокупность векторов не может быть одновременно и линейно зависимой, и
линейно независимой.
Приведём ещё одно определение линейно независимой системы векторов, разумеется, равносильное предыдущему.
Определение 4. Совокупность векторов X будем называть линейно независимой, если
из равенства нулевому вектору их линейной комбинации следует равенство нулю всех коэффициентов этой линейной комбинации, т.е. из равенства следует, что 
.
Замечание. Линейную комбинацию этих векторов можно записать используя определение умножения матриц: 
, где 
, а 
. Тогда определение линейно независимой совокупности векторов можно записать так: 
.
Пример 1. Пусть 
. Очевидно, справедливо равенство: 
. Следовательно, совокупность матриц 
линейно зависимая по определению 3. В этом примере мы рассматриваем матрицы как векторы вещественного линейного пространства 
(R).
|
|
Пример 2. Покажем, что совокупность векторов 
вещественного пространства X = R 
строк длины 
линейно независимая.
Составим линейную комбинацию этих векторов и приравняем её к нулевому вектору:
. Из определения равенства матриц отсюда следует, что 
. Таким образом, по определению 4 эта совокупность линейно независимая.
Пример 3. Покажем, что совокупность матриц 
линейно независимая. Составим линейную комбинацию этих матриц и приравняем её к нулевой матрице:
Легко подсчитать ранг матрицы этой системы: 
. Следовательно, эта система имеет единственное решение, т.е. нулевое (ранг матрицы системы равен числу неизвестных).
Итак, из равенства 
следует, что 
. Следовательно, по определению 4 эта совокупность матриц линейно независимая. В этом примере мы рассматриваем матрицы как векторы вещественного линейного пространства (R).
Пример 4. Множество X = С 
комплексных строк длины 2 является вещественным линейным пространством, потому что такие строки можно складывать и умножать на вещественные числа, и при этом выполняются все 8 аксиом линейного пространства. Покажем, что совокупность строк 
этого пространства линейно независимая. Пусть 
В этой выкладке важно, что числа 
и 
вещественные, т.к. X – вещественное пространство по условию.
Пример 5. Множество X 
= С комплексных строк длины 2 является комплексным линейным пространством, потому что такие строки можно складывать и умножать на комплексные числа, и при этом выполняются все 8 аксиом линейного пространства. Заметим, что пространство X из примера 4и пространство X различные, несмотря на то, что как множества они равны.
|
|
Покажем, что совокупность строк этого пространства линейно зависимая. Действительно, 
,
причём 
.
В предыдущем примере мы не могли взять в качестве коэффициента число 
, т.к. пространство X является вещественным.
Теорема 1. Совокупность векторов линейного пространства, содержащая нулевой вектор, линейно зависима.
Доказательство. Пусть 
-ый вектор в совокупности векторов X нулевой, т.е.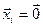 
. Тогда, очевидно, справедливо равенство 
, причём 1- -ый коэффициент не равен 0.
Таким образом, совокупность векторов линейно зависимая по определению 3.
Теорема 2. Если к линейно зависимой совокупности векторов линейного пространства добавить ещё несколько, то получившаяся совокупность будет также линейно зависимая.
Доказательство. Пусть совокупность векторов X линейного пространства над полем K линейно зависимая, т.е. существуют числа K, не равные нулю одновременно и такие, что . Покажем, что тогда совокупность векторов 
X также линейно зависимая.
Действительно, очевидно, справедливо равенство 
, причём не все коэффициенты этой линейной комбинации равны 0, т.к. не все коэффициенты равны нулю. Следовательно, совокупность векторов 
линейно зависимая по определению 3.
Теорема 3. Если из линейно независимой совокупности векторов удалить несколько, то получившаяся совокупность будет также линейно независимой.
Доказательство проведём от противного с использованием теоремы 2. Пусть совокупность векторов X линейно независимая, а совокупность линейно зависимая.
Тогда по теореме 2 исходная совокупность векторов будет также линейно зависимая, что противоречит условию, и теорема доказана.
Теорема 4. Критерий линейной зависимости. Для того чтобы совокупность векторов линейного пространства была линейно зависимой, необходимо и достаточно, чтобы один из векторов этой совокупности был линейной комбинацией остальных.
Доказательство.
Необходимость. Пусть совокупность векторов X линейного пространства над полем K линейно зависимая, т.е. существуют числа K, не равные нулю одновременно и такие, что 
, и пусть для определённости 
. Тогда из последнего равенства получаем:
, и необходимость доказана.
Достаточность. Пусть 
, . Тогда справедливо равенство: 
, причем 
. Следовательно, совокупность векторов линейно зависимая по определению 3, и достаточность доказана.
Теорема 5. Если после добавления к линейно независимой совокупности векторов линейного пространства X над полем K вектора 
X новая совокупность 
становится линейно зависимой, то добавленный вектор 
есть линейная комбинация элементов исходной совокупности, т.е.
ЛК .
Доказательство. По условию совокупность линейно зависимая. Это означает, что существуют числа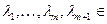 
K, не равные нулю одновременно и такие, что
Покажем, что 
. Пусть это не так, т.е. 
. Из равенства (1) следует, что , причём среди чисел есть ненулевые. Действительно, , а 
не равны нулю одновременно. Из определения 3 следует, что совокупность линейно зависимая, а это противоречит условию.
Таким образом, доказали, что . Тогда из равенства (1) получаем: 
, и теорема 5 доказана.