Условия геометрического и кинематического подобия течений жидкости
Геометрическое подобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственно перед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через kL. Эта величина одинакова (idem) для подобных русел I и II:
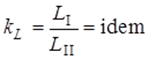
Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей:
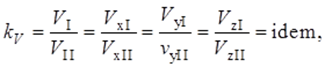
где kV – масштаб скоростей, одинаковый при кинематическом подобии.
Так как

где T – время, kT – масштаб времени.
Очевидно, что для кинематического подобия необходимо геометрическое подобие русел.
Условия динамического подобия течений вязкой жидкости.
Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.
В потоках жидкости обычно действуют разные силы: силы давления, вязкости, тяжести и др. Соблюдение этих пропорциональностей означает полное гидродинамическое подобие. Осуществить полное подобие на практике удается далеко не всегда, поэтому часто имеют дело с частичным (неполным) подобием, при котором пропорциональны только лишь основные, главные силы.
Для напорных течений в закрытых руслах, то есть для потоков в трубах, в гидромашинах и т. п., такими силами являются силы давления, вязкости и инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление: p пр = p + g r h, то есть она учитывается.
Для гидродинамического подобия потоков необходимо, чтобы

Это отношение называют числом Ньютона и обозначают Ne. Под силой F здесь понимается основная сила: сила давления, вязкости, тяжести или др. То есть это общий вид закона гидродинамического подобия.
Рассмотрим три характерных случая воздействия на движущуюся жидкость основных сил и найдем условия подобия потоков.
1. На жидкость действуют лишь силы давления и инерции. Тогда F = D pS ~ D pL2 и условие гидродинамического подобия примет вид:

где D p – разность давлений или просто давление,
Eu – безразмерный критерий, число Эйлера.
Таким образом, в этом случае условием гидродинамического подобия потоков является равенство чисел Эйлера, которые равны величине, пропорциональной отношению сил давления к силам инерции.
2. На жидкость действуют силы вязкости, давления и инерции. Тогда

Условие гидродинамического подобия потоков после деления на r V 2 L 2 примет вид:

где Re – безразмерный критерий, называемый числом Рейнольдса.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.
3. На жидкость действуют силы тяжести, давления и инерции. Тогда F ~ g r L 3 и условие гидродинамического подобия потоков примет вид:

где Fr – безразмерный критерий, число Фруда.
Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Фруда. Из вывода видно, что число Фруда – это величина, пропорциональная отношению силы инерции к силе тяжести. Этот критерий важен при рассмотрении безнапорных течений в открытых руслах, для напорных течений его можно не учитывать.