ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ОБЪЁМЕ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

 

Кафедра «Физика»

 

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ

ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ОБЪЁМЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ № 144

по дисциплине «Физика»

 

Под редакцией профессора Марченко В.И.

 

 

МОСКВА – 2011

 

 

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

 

Кафедра «Физика»

 

 

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ

ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ОБЪЁМЕ

 

 

Под редакцией профессора В.И. Марченко

 

 

Рекомендовано редакционно-издательским советом

университета в качестве методических указаний для студентов ИУИТ, ИТТСУ и ИПСС

 

 

МОСКВА - 2011

 

 

УДК 531.53

Л-90

 

Р.М. Лагидзе, Ю.Н. Харитонов, А.М. Куюмчян. Определение отношения теплоёмкостей воздуха при постоянном давлении и объёме. Методические указания к лабораторной работе № 144 по дисциплине «Физика» / под ред. проф. В.И. Марченко – М.: МИИТ, 2011. – 13 с.

 

 

Методические указания к выполнению лабораторной работы № 144 «Определение отношения теплоёмкостей воздуха при постоянном давлении и объёме» соответствуют программе и учебным планам по физике (раздел «Молекулярная физика») и предназначены для студентов 1, 2 курсов технических специальностей.

 

 

© Московский государственный

университет путей сообщения

(МИИТ), 2011

 

Работа 144

 

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЁМКОСТЕЙ ВОЗДУХА

ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ОБЪЁМЕ

 

Цель работы: Определение отношения теплоёмкости воздуха при постоянном давлении к теплоёмкости при постоянном объёме.

Приборы и принадлежности: установка ФПТ1-6, общий вид которой приведён на рис. 3.

 

Введение

 

Удельной теплоемкостью вещества называется величина, равная количеству теплоты, которую необходимо сообщить единице массы вещества для увеличения её температуры на один Кельвин:

с = .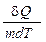

Молярной теплоёмкостью (или теплоёмкостью одного моля вещества) называется величина, равная количеству теплоты, которую необходимо сообщить одному молю вещества для увеличения его температуры на один Кельвин:

C = c μ = = ,

где m – масса; m – масса одного моля вещества, n = – число молей.

В СИ удельная теплоёмкость выражается в Дж/кг∙К, а молярная – в Дж/моль∙К.

Численное значение теплоёмкости зависит от природы газа и процесса нагревания.

Согласно первому закону термодинамики количество теплоты δ Q, сообщенное системе, расходуется на увеличение внутренней энергии dU и на выполнение системой работы δ A против внешних сил:

 

δ Q = dU + δ A. (1)

 

Увеличение внутренней энергии идеального газа при увеличении его температуры на dT:

dU = RdT, (2)

где i – число степеней свободы молекулы, под которым подразумевается число независимых координат, определяющих положение молекулы в пространстве: i = 3 – для одноатомных; i = 5 – для двухатомных; i = 6 – для трёх- и многоатомных молекул; R – универсальная газовая постоянная; R =8,31 Дж/(моль·К).

При расширении газа он выполняет работу:

 

δ A = PdV.

 

Если газ нагревать при постоянном объёме V = const, то δ А = 0, и согласно (1) все полученное газом количество теплоты расходуется только на увеличение его внутренней энергии (dQ_V = dU), и, учитывая (2), молярная теплоемкость идеального газа при постоянном объеме:

 

C _V = = (i /2) R.

Если газ нагревать при постоянном давлении P = const, то полученное газом количество теплоты расходуется на увеличение внутренней энергии dU и выполнение работы δ А:

 

δ Q = dU + PdV.

 

Тогда молярная теплоемкость идеального газа при постоянном давлении:

C _P = + .

Используя уравнение состояния идеального газа (уравнение Клапейрона – Менделеева),

PV = RT,

можно доказать, что для одного моля газа

 

P = R,

 

и поэтому молярная теплоемкость при P = const:

 

C _P = R.

Для отношения теплоёмкостей g можно записать:

g = = . (3)

 

 

Методика измерений

 

Для определения отношения С _Р/ C _V для воздуха в данной лабораторной работе применен метод, предложенный Клеманом и Дезормом, в котором использовано охлаждение газа при его адиабатическом расширении. Предполагается, что воздух – идеальный газ.

Адиабатическим называется процесс, который происходит без теплообмена с окружающей средой. Быстрое сжатие и быстрое расширение газа приблизительно можно рассматривать как адиабатический процесс.

Согласно первому закону термодинамики (1) для адиабатического процесса:

0 = dU + δA.

Откуда δA = -dU = - RdT.

 

Из последнего уравнения видно, что при адиабатическом сжатии температура газа повышается за счёт работы внешних сил (δA<0), а при адиабатическом расши­рении (δA>0) температура газа понижается, т.к. часть внутренней энергии газа расходуется на работу по расширению газа.

Рисунки 1 и 2 поясняют метод Клемана и Дезорма.

На рисунке 1 изображён лабораторный стенд, который состоит из стеклянного баллона Б, наполнённого воздухом и соединённого с водяным манометром М. Посредством крана К баллон может сообщаться с атмосферой. Первоначально в баллоне было атмосферное давление Р_А и температура T_А, равная температуре окружающей среды.

 

 

Рис. 1

 

Рис. 2

 

Если с помощью насоса Н подкачать в баллон некоторое количе­ство воздуха, то давление в баллоне повысится до значения Р ₁. Манометрический водя­ной столбик не сразу займет окончательное положение, так как при бы­стром сжатии температура повышается. Благодаря теплопроводности стенок сосуда через некоторое время температура воздуха в баллоне сравняется с температурой воздуха окружающей среды. Это состояние газа характеризуется температурой Т ₁ = Т _А, и давлением Р ₁ (на рис. 2 точка 1). Давление Р ₁ равно сумме первоначального давления газа в баллоне Р _А и избыточного давления газа в баллоне D Р ₁:

 

Р ₁ = Р _А + D Р ₁.

 

После того как давление газа в баллоне установилось, открывается кран и воздух адиабатически расширяется, выходя в атмосферу. В тот момент, когда давление воздуха в баллоне становится равным атмосферному (высота столбиков воды в обоих коленах манометра сравни­вается), кран быстро закрывается. При расширении температура газа в баллоне понижается. Это состояние представлено точкой 2 на рис. 2. В первоначальный момент температура ниже Т _А окружающей среды. Через некоторое время после закрытия крана температура воздуха в баллоне повышается до температуры Т _А за счет теплообмена с окружающей средой, а давление в баллоне при этом повысится на величину избыточного давления D Р ₂.

Состояние газа будет характеризоваться температурой Т ₁ и давлением:

Р ₃ = Р _А + D Р ₂.

 

Это состояние представлено точкой 3 на рис. 2. Таким образом, процесс перехода газа из состояния 1 в состояние 2 происходит адиабатически, а из состояния 2 в состояние 3 изохорически. Точки 1 и 3 диаграммы лежат на одной изотерме. Адиабатическое расширение при переходе из состояния 1 в состояние 2 описывается уравнением Пуассона:

Р ₁ = Р ₂ . (4)

 

Для изохорического процесса при переходе газа из состояния 2 в состояние 3 имеем:

= . (5)

 

Из уравнений (4) и (5), исключив T₂/T₁, получим:

 

= (6)

 

Логарифмируя выражение (6), получим:

 

(1 - g) (lgP ₁ - lgP ₂) = g(lgP ₂ - lgP ₃).

 

откуда

g = .

 

Заменив Р ₁, Р ₂ и Р ₃ на Р ₁ = Р _А + D Р ₁, Р ₂ = Р _А, Р ₃ = Р _А + D Р ₂,

получим:

g = .

 

Учитывая, что D lgx » D х / х, если D х малая по сравнению с х величина, имеем (D Р ₁ и D Р ₂ малы по сравнению с Р _А):

g = .

 

Учитывая также, что D Р = r g D h, где D h - разница высот столбиков воды в манометре, окончательно получаем:

 

g = . (7)