Конструкторский раздел
Структура системы контроля на основе оптимального оценивающего фильтра
При практической реализации диагностических моделей на основе наблюдателей параметров состояния необходимо учитывать следующие особенности реальных объектов контроля.
Нелинейная взаимосвязь входных и выходных сигналов объекта контроля;
Нелинейная взаимосвязь сигналов объекта контроля и наблюдений;
Влияние возмущений на входные и выходные сигналы объекта контроля, а также на наблюдателя.
Поэтому возникает необходимость построения стохастических диагностических моделей. Технология формирования таких моделей опирается на математическое описание функционирования эталонного и реального объектов контроля. Таким ОК ставятся в соответствие идеальный 
и реальный 
векторы параметров состояния, которые описываются следующими дифференциальными уравнениями:
для идеального ОК: 
; (%1)
для идеального ОК: 
(%2)
где 
– вектор погрешностей действующий на ОК, характеризующийся ковариационной матрицей;
Параметры реального и идеального ОК связаны через уравнение ошибок. Для получения уравнения ошибок вычтем из соотношения (%2) выражение (%1) и разложим функцию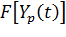 
в ряд Тейлора относительно параметров идеального ОК, тогда
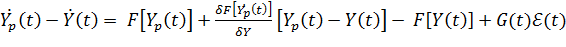(%3)
Обозначим 
– вектор ошибок ОК;
– матрица коэффициентов, характеризующих динамику изменения ошибок ОК (фундаментальная матрица динамической системы).
Тогда из соотношения (%3) можно получить следующее уравнение ошибок:
(%4)
Аналогичным образом можно определить взаимосвязь наблюдаемых параметров с ошибками ОК. Наблюдаемые параметры реального объекта контроля (ОКР) описываются уравнением
. (%5)
Модель внешнего по отношению к ОКР наблюдающего устройства имеет вид 
, (%6)
где 
– вектор возмущений в канале наблюдения.
– вектор наблюдений, формируемых эталонной по отношению к ОКР системой.
Вычитая из соотношения (%5) выражение (%6) и разложив функцию 
в ряд Тейлора относительно параметров идеального ОК, получим
(%8)
Обозначим 
– вектор наблюдений;
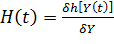– матрица связи наблюдаемых параметров с вектором ошибок ОКР.
Тогда из уравнения (%8) можно получить модель наблюдения ошибок ОКР (модель сигналов)
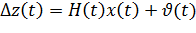(%10)
С учетом уравнений (%4) и (%10) сформируем алгоритм оптимального оценивания ошибок ОКР.
Алгоритм оптимального оценивания ошибок динамических объектов контроля в дискретном времени
На практике наблюдения 
, отражающие состояние объекта контроля, формируются в дискретные моменты времени 
и обозначается 
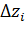. Для получения оптимальных оценок вектора ошибок ОКР по наблюдениям 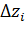применяют дискретный оптимальный фильтр Калмана. Для реализации такого фильтра необходимо определить динамику изменения оценок 
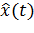и ковариационных матриц 
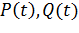за время 
между моментами наблюдений 
и 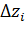. Переходные матрицы 
и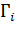 
для прогнозирования указанных параметров находятся из решения дифференциального уравнения (%4). Для однородной части этого уравнения при неизменной матрице 
на интервале прогноза решение определяется следующими отношениями:
(%32)
(%33)
, (%34)
где 
– переходная матрица для вектора ошибок, удовлетворяющая следующему дифференциальному уравнению.
(%35)
При 
. (%36)
Для определения переходной матрицы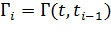 
для вектора возмущений 
покажем сначала, что решение неоднородного уравнения (%4) имеет вид
. (%37)
Дифференцируя соотношение (%37) по аргументу 
и применяя правило Лейбница к интегралу свертки, а именно:
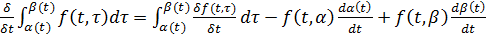(%38)
Получим
. (%39)
С учетом равенства (%35) и условия (%36) соотношение (%39) можно привести к следующему виду:
(%40)
Можно видеть, что подстановка решения (%37) в соотношение (%40) приводит к уравнению, эквивалентному (4). В выражении (%37) можно ввести следующее обозначение:
(%42)
Тогда, дифференцируя интеграл свертки (%42) по правилу (%38) и учитывая соотношения (%35), (%36), получим дифференциальное уравнение для переходной матрицы вектора возмущений ОКР.
при 
. (%43)
Таким образом, уравнение ошибок ОК (4) будет иметь вид
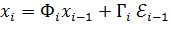, (%44)
С учетом решения (%37) значения оценок 
вектора ошибок ОК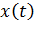 
и его ковариационной матрицы 
на интервале прогноза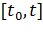 
будут определяться следующими соотношениями:
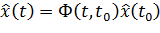(%45)
. (%46)
Соотношение (%46) сформировано с учетом некоррелированности начальных ошибок оценивания и шумов ОК, т.е. 
для 
.
Для того, чтобы гарантировать попадание точки, в которой наблюдается всплеск дельта-функции, в область интегрирования, необходимо вначале интегрировать по переменной, имеющей больший диапазон. В частности, при 
необходимо выражение (%46) сначала проинтегрировать по 
. В этом случае соотношение (%46) с учетом свойств дельта-функции (%27) можно представить в следующем виде:
(%47)
Свойства оптимального фильтра Калмана позволяют реализовать на его основе диагностические модели как сигнального, так и параметрического типа. Ядром таких моделей являются уравнения наблюдений и ошибок объекта контроля. При этом должны учитываться следующие особенности включения ОФК в структуру системы контроля:
- необходимо одновременно решать нелинейные динамические уравнения ОК и линеаризованные уравнения его ошибок;
- ОФК должен функционировать в условиях априорной неопределённости относительно структуры и параметров диагностических моделей ОК, а также статистических характеристик возмущений и шумов.
В настоящее время ОФК составляет ядро программно-математического обеспечения современных навигационных комплексов. Это создает необходимую основу для расширения функциональных возможностей ОФК на решение задач контроля и диагностики.