САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА
ВЫСШЕЙ МАТЕМАТИКИ И ИНФОРМАТИКИ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ УПРАВЛЕНИЯ
КОМПЬЮТЕРНЫЕ МЕТОДЫ
ПРИНЯТИЯ РЕШЕНИЙ
Методические указания
К выполнению лабораторных работ
| Составители: Д.ф.–м.н., профессор Сараев Л.А. К.ф.–м.н., доцент Ильина Е.А. |
САМАРА 2006
СОДЕРЖАНИЕ
1. МАТЕМАТИЧЕСКИЕ МЕТОДЫПРИНЯТИЯ РЕШЕНИЙ. 3
Задание 1.1. Задача линейного программирования о смесях. 3
Задание 1.2. Транспортная задача. 5
Задание 1.3. Задача целочисленного программирования. 6
2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.. 7
Задание 2.1. 7
Задание 2.2. 7
Задание 2.3. 7
Задание 2.4. 7
Задание 2.5. 8
Задание 2.6. 8
Задание 2.7. 8
Задание 2.8. 8
Задание 2.9. 8
Задание 2.10. 8
Задание 2.11. 9
Задание 2.12. 9
Задание 2.13. 9
Задание 2.14. 9
Задание 2.15. 10
Задание 2.16. 10
Задание 2.17. 10
Задание 2.18. 10
Задание 2.19. 10
Задание 2.20. 11
Задание 2.21. 11
Задание 2.22. 11
Задание 2.23. (Задача о расписании полетов) 11
ЛИТЕРАТУРА.. 12
Методические указания к выполнению лабораторных работ по информационным технологиям управления «Компьютерные методы принятия решений» предназначены для студентов очного и заочного отделений СамГУ для всех специальностей.
МАТЕМАТИЧЕСКИЕ МЕТОДЫПРИНЯТИЯ РЕШЕНИЙ.
Планирование правовой, производственно-хозяйственной, управленческой и административной деятельности приводит к задачам, имеющим множество допустимых решений. Из этого множества решений нужно уметь выбрать такое, которое бы оптимальным образом учитывало внутренние возможности и внешние условия для хозяйствующего или управляющего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и т.д.).
Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение 
, где 
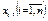– его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
Для этого нужно выбрать некоторый критерий оптимальности экономического или правового показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений («максимум прибыли», «минимум затрат», «максимум рентабельности» и т.д.).
При этом выбор планово-управленческого решения осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
На практике принцип оптимальности в планировании и управлении означает решить экстремальную задачу вида об отыскании максимума или минимума функции
при ограничениях
Вектор называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А то допустимое решение , которое доставляет максимум или минимум целевой функции , называется оптимальным планом (решением) задачи.
Если функция является линейной, а система ограничений представляет собой систему линейных неравенств, то такая задача называется задачей линейного программирования.
Предлагаемые далее задания разделены на три группы:
· экономические задачи линейного программирования,
· транспортные задачи,
· задачи целочисленного программирования.
В начале показаны образцы решений всех трех типов заданий, а затем предложены задания для самостоятельного решения.